当前位置:网站首页>【LeetCode】最长公共子序列(动态规划)
【LeetCode】最长公共子序列(动态规划)
2022-08-03 23:00:00 【小七mod】
一、题目
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace" 输出:3 解释:最长公共子序列是 "ace" ,它的长度为 3 。
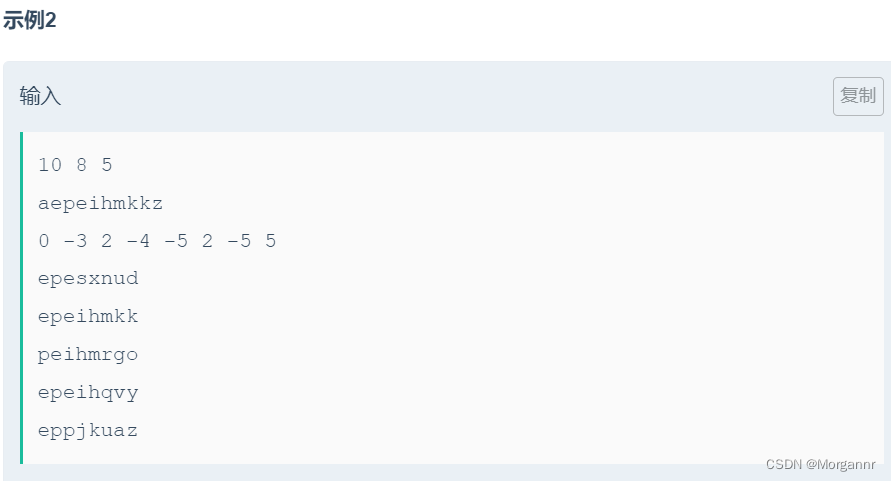
示例 2:
输入:text1 = "abc", text2 = "abc" 输出:3 解释:最长公共子序列是 "abc" ,它的长度为 3 。
示例 3:
输入:text1 = "abc", text2 = "def" 输出:0 解释:两个字符串没有公共子序列,返回 0 。
提示:
1 <= text1.length, text2.length <= 1000text1和text2仅由小写英文字符组成。
二、代码
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
if (text1 == null || text1.length() == 0 || text2 == null || text2.length() == 0) {
return 0;
}
char[] str1 = text1.toCharArray();
char[] str2 = text2.toCharArray();
int[][] dp = new int[str1.length][str2.length];
dp[0][0] = str1[0] == str2[0] ? 1 : 0;
for (int j = 1; j < str2.length; j++) {
dp[0][j] = str1[0] == str2[j] ? 1 : dp[0][j - 1];
}
for (int i = 1; i < str1.length; i++) {
dp[i][0] = str1[i] == str2[0] ? 1 : dp[i - 1][0];
}
for (int i = 1; i < str1.length; i++) {
for (int j = 1; j < str2.length; j++) {
int p1 = dp[i - 1][j];
int p2 = dp[i][j - 1];
int p3 = str1[i] == str2[j] ? dp[i - 1][j - 1] + 1 : dp[i - 1][j - 1];
dp[i][j] = Math.max(p1, Math.max(p2, p3));
}
}
return dp[str1.length - 1][str2.length - 1];
}
}边栏推荐
- Scala basics [regular expressions, framework development principles]
- 直播预告 | 构建业务智联,快速拥抱财务数字化转型
- With 4 years of work experience, the 5 communication methods between multi-threads can't be said, can you believe it?
- Research status of target detection at home and abroad
- Testng listener
- 伴随着元宇宙、web3.0等概念的兴起,数字人、数字场景等诸多数字化的形态开始出现
- rosbridge-WSL2 && carla-win11
- complete binary tree problem
- Cloud platform construction solutions
- What is Adobe?
猜你喜欢
随机推荐
Pytest学习-setup/teardown
藏宝计划TreasureProject(TPC)系统模式开发技术原理
Click the icon in Canvas App to generate PDF and save it to Dataverse
V8中的快慢数组(附源码、图文更易理解)
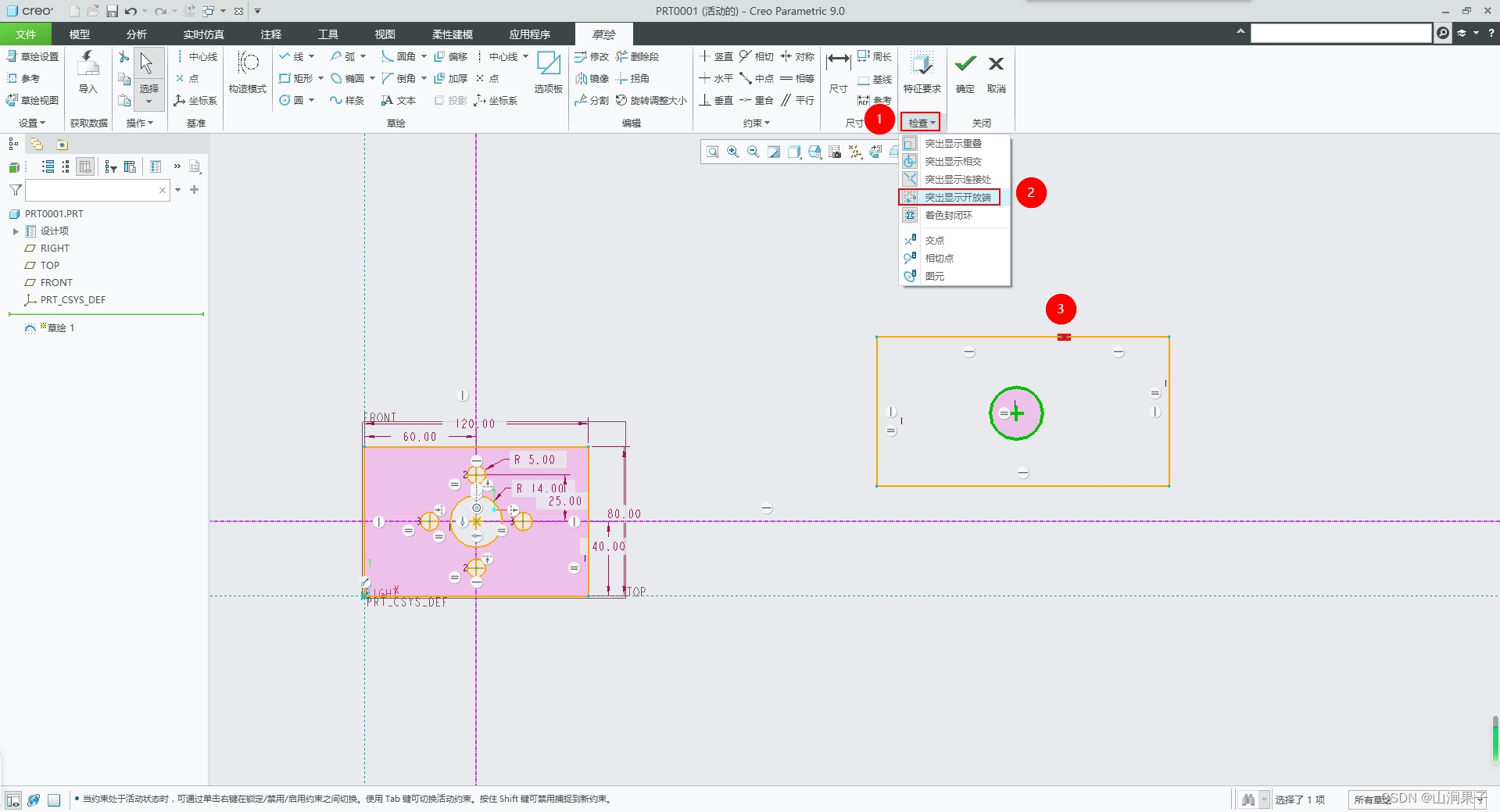
Creo 9.0创建几何点
Websocket multi-threaded sending message error TEXT_PARTIAL_WRITING--Use case of spin lock replacing synchronized exclusive lock
什么是memoization,它有什么用?
【day1】
举一个 web worker 的例子
重发布实验报告
SPOJ 2774 Longest Common Substring(两串求公共子串 SAM)
Zilliz 2023 秋季校园招聘正式启动!
如何创建一个Web项目
utlis thread pool
IELTS essay writing template
Makefile
电商秒杀系统
Redis persistence method
Live Preview | Build Business Intelligence, Quickly Embrace Financial Digital Transformation
【bug】汇总Elipse项目中代码中文乱码解决方法!