当前位置:网站首页>Code Casual Recording Notes_Dynamic Programming_416 Segmentation and Subsetting
Code Casual Recording Notes_Dynamic Programming_416 Segmentation and Subsetting
2022-08-03 22:50:00 【Erik_Won】
代码随想录笔记_动态规划
代码随想录二刷笔记记录
LC416.分割等和子集
题目
01背包
给你一个 只包含正整数 的 非空 数组 nums .请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等.
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] .
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集.
思路分析
思路:
Divide the array into two subsets,make subset A 和子集 B the sum is equal
-> Find the set appears sum/2 的Subset sum.can be divided into two equal subsets
加入01背包的概念
1.背包的容量 sum/2
2.The weight of the item that needs to be put in the backpack is the value of the elementnums[i],价值也是nums[i]
3.背包如果正好装满,Indicates that equal subsets were found
4.Every element in the backpack is non-repeatable
动态规划五部曲
1.确定dp数组及其下标含义
dp[j]:Represents the sum of one of the subsets that makes the two subsets equal.
简单地说就是(符合题意)Subset sum
2.确定递推公式
dp[j] = max(dp[j],dp[j-nums[i]] + nums[i])
The weight and value of the items in this question are both nums[i]
3.初始化
Known from knowledge of rolling arrays,numThe elements in are all positive integers,则dp初始化为0即可.
Only all are initialized to0,The maximum value can only be taken during derivation.
反之,如果 num The elements in have negative numbers,则dp中的非0Subscript elements need to be initialized to negative infinity.
4.遍历顺序
for(int i = 0;i < nums.length;i++){
//先遍历物品,That is, the array value
for(int j = target; j >= nums[i];j --){
//遍历背包容量
//注意,Each element can only be placed once,Hence the reverse order,Avoid replay
dp[j] = max(dp[j],dp[j - nums[i]] + nums[i]);
}
}
5.推演分析
以 [1,5,5,11] 为例
| 容量 j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 元素1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 元素5 | 0 | 1 | 1 | 1 | 1 | 5 | 6 | 6 | 6 | 6 | 6 | 6 |
| 元素5 | 0 | 1 | 1 | 1 | 1 | 5 | 6 | 6 | 6 | 6 | 6 | 11 |
图示:

代码实现
完整代码实现
public boolean canPartition(int[] nums) {
if (null == nums || nums.length == 0) return false;
// num 求和
int sum = Arrays.stream(nums).sum();
// 如果 sum 为奇数,Indicates that no two identical subsets could be found
if (sum % 2 == 1) return false;
// 背包容量
int bagSize = sum /2;
// 初始化dp数组
int[] dp = new int[bagSize + 1];
for (int i = 0; i < nums.length; i++) {
// 遍历元素
for (int j = bagSize; j >= nums[i]; j--) {
// 遍历背包
dp[j] = Math.max(dp[j],dp[j - nums[i]] + nums[i]);
}
}
return bagSize == dp[bagSize];
}
边栏推荐
- 剑指offer第22题-链表中倒数第K个节点
- HCIP BGP lab report
- MiniAPI of .NET6 (14): Cross-domain CORS (Part 1)
- 直播预告 | 构建业务智联,快速拥抱财务数字化转型
- Shell编程的条件语句
- 云计算国内外发展现状
- Gains double award | know micro easily won the "2021 China digital twin solution suppliers in excellence" "made in China's smart excellent recommended products" double award!
- How many way of calling a function?
- FinClip最易用的智能电视小程序
- 生成器版和查看器版有什么区别?
猜你喜欢

藏宝计划TreasureProject(TPC)系统模式开发技术原理
October 2019 Twice SQL Injection
亿流量大考(2):开发一套高容错分布式系统
Republish the lab report
![navicat 连接 mongodb 报错[13][Unauthorized] command listDatabases requires authentication](/img/09/a579c60e07cdc145175e72673409f7.png)
navicat 连接 mongodb 报错[13][Unauthorized] command listDatabases requires authentication

Another MySQL masterpiece published by Glacier (send the book at the end of the article)!!
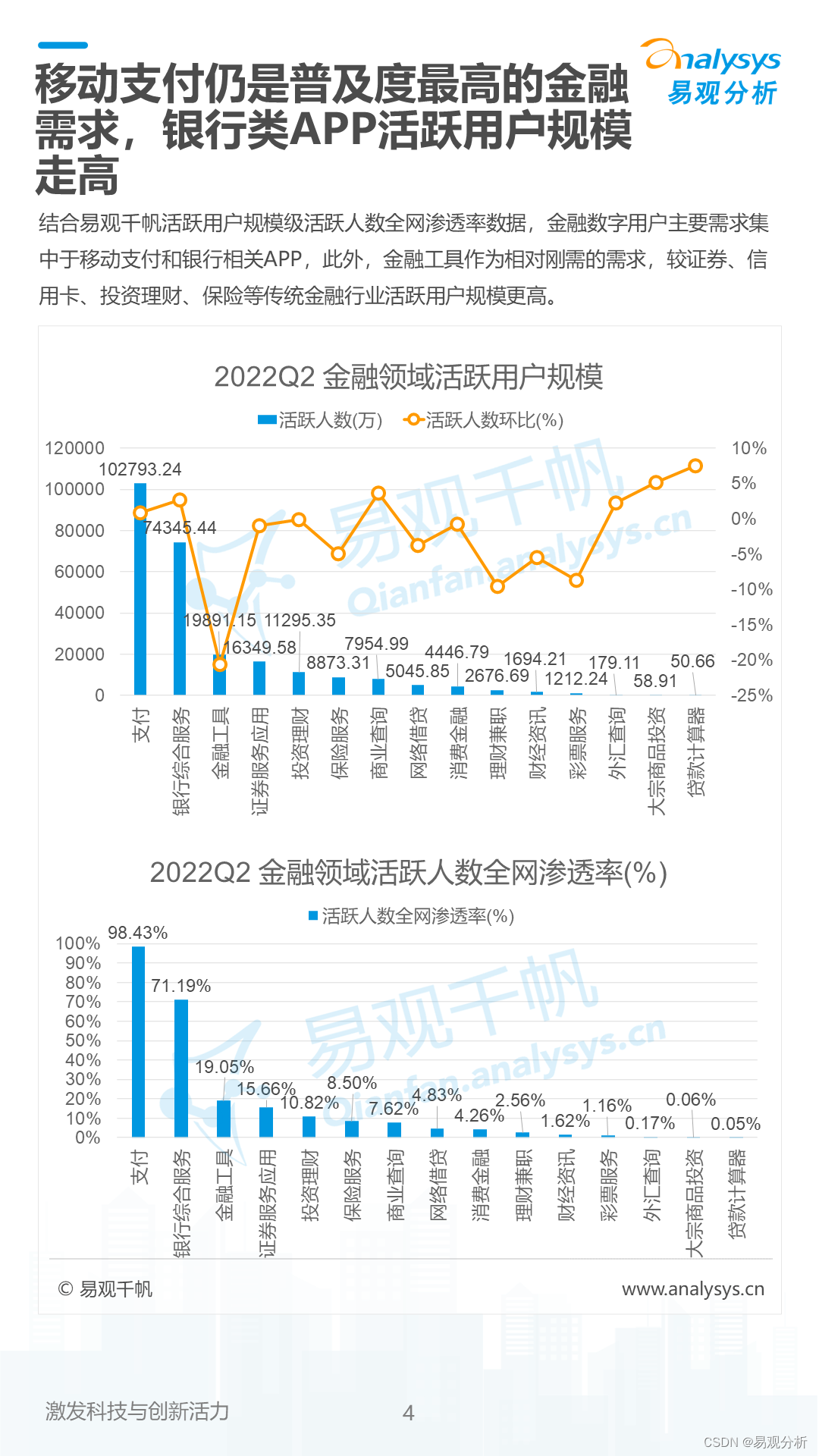
《数字经济全景白皮书》金融数字用户篇 重磅发布!
静态文件快速建站
pikachu Over permission
电商秒杀系统
随机推荐
Pytest learn-setup/teardown
LabVIEW code generation error 61056
软件测试内卷严重,如何提升自己的竞争力呢?
pikachu Over permission
2022-08-03 Oracle executes slow SQL-Q17 comparison
【day6】类与对象、封装、构造方法
"Digital Economy Panorama White Paper" Financial Digital User Chapter released!
ML's yellowbrick: A case of interpretability (threshold map) for LoR logistic regression model using yellowbrick based on whether Titanic was rescued or not based on the two-class prediction dataset
Cloud platform construction solutions
utlis 线程池
Cisco ike2 IPSec configuration
node连接mysql数据库报错:Client does not support authentication protocol requested by server
First domestic open source framework 】 【 general cloud computing framework, any program can be made into cloud computing.
win10系统下yolov5-V6.1版本的tensorrt部署细节教程及bug修改
如何创建一个Web项目
On the Qixi Festival of 2022, I will offer 7 exquisite confession codes, and at the same time teach you to quickly change the source code for your own use
一个函数有多少种调用方式?
云计算国内外发展现状
PowerMockup 4.3.4::::Crack
【MySQL进阶】数据库与表的创建和管理