当前位置:网站首页>378. 有序矩阵中第 K 小的元素
378. 有序矩阵中第 K 小的元素
2022-06-11 01:07:00 【Melody2050】
二分查找思路
题目 https://leetcode.cn/problems/kth-smallest-element-in-a-sorted-matrix/
官方题解 https://leetcode.cn/problems/kth-smallest-element-in-a-sorted-matrix/solution/you-xu-ju-zhen-zhong-di-kxiao-de-yuan-su-by-leetco/
利用二分查找,去找到那个第k大的数字。首先设置左右区间,left为左上角,right为右下角。mid为两者平均值。

假设取mid=8,从左下角开始,沿着蛇形路线找出所有不小于mid的数。计算这样的数有几个(6+6+4+2=18)。

然后,比较它与k。如果中间值取太大了,则应当寻找左半区间,否则应当寻找右半区间。
图例
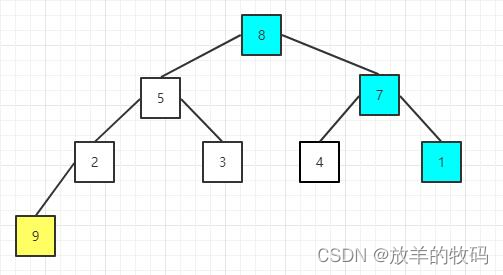
以下图为例,矩阵中有[…, 1, 3, 6, 10]这些数,第k个数是3。将矩阵中的数字有序铺开于下图。刚开始,left和right分处图两端。当mid取到红色区间时,会触发left = mid + 1;矩阵会往右侧收缩,否则,矩阵取到蓝色区间时,触发right=mid,矩阵会往左侧收缩,但这里要确保mid<right,才能保证矩阵能够往左侧收缩。
另外一个细节是,尽管答案是3,当mid取到3、4和5时,计算不小于mid的数都等于k。所以,我们要确保rank >= k时,都让区间向左侧收缩,直到左右界都收敛到3这个点为止。
代码
代码如下:
class Solution {
public int kthSmallest(int[][] matrix, int k) {
int n = matrix.length;
int left = matrix[0][0], right = matrix[n-1][n-1];
while (left < right) {
int mid = left + (right - left) / 2;
if (binarySearch(matrix, k, mid)) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
public boolean binarySearch(int[][] matrix, int k, int mid) {
int n = matrix.length;
int i = n-1, j = 0;
int rank = 0;
while (i >= 0 && j <= n-1) {
if (matrix[i][j] <= mid) {
rank += i + 1;
j++;
} else {
i--;
}
}
return rank >= k;
}
}
需要注意的细节有两个。
第一个细节是,计算中位值时使用:
int mid = left + (right - left) / 2;
而不使用
int mid = (left + right) / 2;
因为,尽管后者在计算正数时,能保证mid < right,比如当left和right取[3, 4]时,mid=3。但在计算负数时,会取到右侧,比如[-4, -3]时,mid=-3。
而前者不论计算正数还是负数,都能保证mid<right,从而令区间能向左侧收缩。
第二细节是,区间最终要收敛到一个点,即只要满足rank>=k,区间都应该向左收缩,直到收敛到一个点为止。否则如上图,3 4 5都能满足rank>=k都能取到,选择4或者5就错了。
边栏推荐
- 安全生产月知识竞赛——新安法知多少
- 可扩/减容线程池C语言原理讲解及代码实现
- 渗透测试-安全服务体系+OWASP top 10
- Asemi FET 12n65 parameters, 12n65 specifications, 12n65 features
- Day code 300 lines learning notes day 22
- ME11/ME12采购信息记录及条件记录创建及更新BAPI:ME_INFORECORD_MAINTAIN_MULTI
- [BSP video tutorial] BSP video tutorial issue 17: single chip microcomputer bootloader topic, startup, jump configuration and various usage of debugging and downloading (2022-06-10)
- Merge sort ()
- [music] playing "over fire" based on MATLAB [including Matlab source code 1875]
- Secret
猜你喜欢

大厂测试员年薪30万到月薪8K,吐槽工资太低,反被网友群嘲?
![[3.delphi common components] 7 timer](/img/3c/b983575c93d7408a64a59c931ad991.jpg)
[3.delphi common components] 7 timer

腾讯面试官曰Mysql架构的内部模块索引原理及性能优化思路谁会?
![[C language] storage of data in memory -1 plastic](/img/4a/24c1bb4743bd4ae965ed88f333f2fe.jpg)
[C language] storage of data in memory -1 plastic
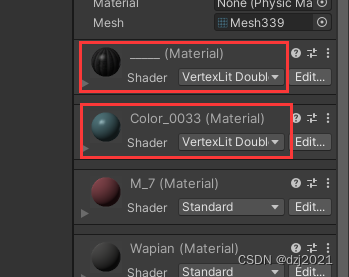
双面材质【double sided】的Shader

Method of using dism command to backup driver in win11 system

Project sorting of Online Exercise System Based on gin and Gorm
ACM tutorial - heap sorting

The interviewer of Tencent said that who knows the internal module index principle and performance optimization idea of MySQL architecture?

Asemi FET 12n65 parameters, 12n65 specifications, 12n65 features
随机推荐
渗透测试-安全服务体系+OWASP top 10
JS basic part hand exercises
Start with interpreting the code automatically generated by BDC, and explain the trial version of the program components of sapgui
Find - (half find / half find)
【Qt】error: QApplication: No such file or directory 解决方案
[3.delphi common components] 6 scroll bar
Return function of different return values
20n10-asemi medium and small power MOS transistor 20n10
大厂测试员年薪30万到月薪8K,吐槽工资太低,反被网友群嘲?
Oracle tablespaces, users, and authorization to users
Task04: String
CRS-4544 & ORA-09925
27岁女生零基础转行软件测试,合适吗?
双面材质【double sided】的Shader
Oracle collects statistics
SAP smartforms text content manual wrap output
Find - (block find)
Using an old mobile phone to build a server and achieve intranet penetration does not require root (I have personally tested the simplest one many times)
Me11/me12 purchase information record and condition record creation and update bapi:me_ INFORECORD_ MAINTAIN_ MULTI
[untitled]