[leetcode] dynamic programming solution split integer i[silver fox]

Welcome to 、 give the thumbs-up 、 forward 、 subscribe , Between your hands , My power source .

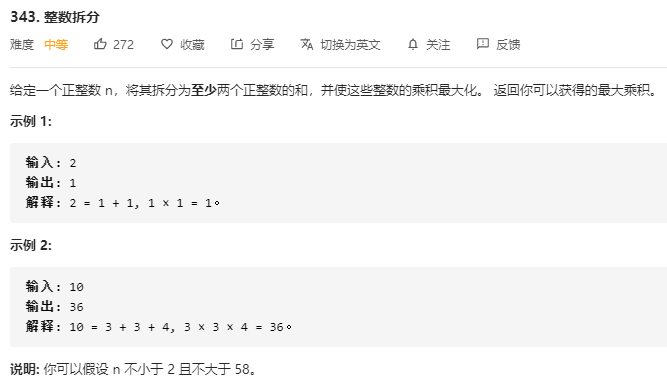
Define the State

$dp[i]$ It means that you will $i$ Split into at least 2 After the sum of positive integers , The product of these integers

Transfer equation

First, consider the general situation ：

• $dp[0]$ There's no point , Because the subscript is from 0 Start , This value appears , Set it to 0

• $dp[1]$ 1 Cannot be split into smaller positive integers again , Set it to 0

• $dp[2]$,2 There is just one way to dismantle it , Split it into two 1,$dp[2]$=1*1=1

• …

• $dp[i]$, reflection $dp[i]$, It is conceivable that within its scope , We have already dismantled one $j$, from $[1...j]$ As a whole 1, See the scenario below 1, The rest is $[j+1....i]$, There are two options

  • Continue as a whole , For the whole 2, Its value is $i-j$, obviously $dp[i]$=$j$X$(i-j)$
  • Continue splitting , But we don't know how many pieces we can split , But we don't care , The result of splitting is $dp[i-j]$（ Read the definition of state again ）, See the scenario below 2,$dp[i]$=$j$X$dp[i-j]$
  • therefore $dp[i]$=$j$X$max(i-j,dp[i-j])$

• $dp[n]$, Value to return

The border

As discussed above

Complete code

    public int integerBreak(int n) {
    
        int[] dp = new int[n + 1];
        for (int i = 2; i <= n; i++) {
    
            for (int j = 1; j < i; j++) {
    
                dp[i] = Math.max(dp[i], j * Math.max(i - j, dp[i - j]));
            }
        }
        return dp[n];
    }