当前位置:网站首页>leetcode/submatrix element sum
leetcode/submatrix element sum
2022-08-01 11:03:00 【xcrj】
思路
二维前缀和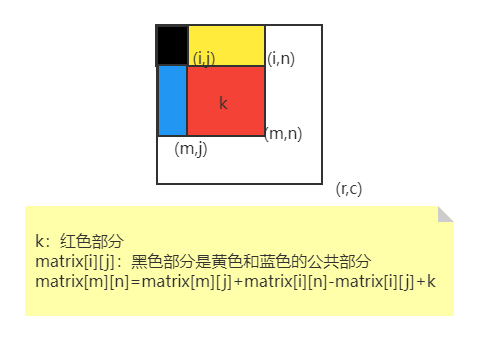
代码
package com.xcrj;
/** * 给定一个二维矩阵 matrix,计算其子矩形范围内元素的总和 * 已知:该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2) . */
public class Solutions13 {
/** * 一维前缀和 * preSum[j]+k=preSum[i], kIs the child matrix row and */
static class NumMatrix1 {
// All rows prefix and
int[][] preSum;
public NumMatrix1(int[][] matrix) {
// All rows prefix and
preSum = new int[matrix.length][matrix[0].length + 1];
// There is no any element prefix and as0
for (int i = 0; i < matrix.length; i++) {
preSum[i][0] = 0;
}
// For all the rows prefix and
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
// preSum[i][1], Prefix and have1个元素时
preSum[i][j + 1] = preSum[i][j] + matrix[i][j];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
int sumK = 0;
// 遍历所有行 O line prefix and 的和
for (int i = row1; i <= row2; i++) {
// Each row of the prefix and
sumK += preSum[i][col2 + 1] - preSum[i][col1];
}
return sumK;
}
}
/** * 二维前缀和 * 2*preSum[i][j]+k=preSum[i][n]+preSUm[m][j] */
static class NumMatrix2 {
// 二维前缀和
int[][] preSum;
public NumMatrix2(int[][] matrix) {
// All rows prefix and
preSum = new int[matrix.length + 1][matrix[0].length + 1];
// There is no any element prefix and as0
preSum[0][0] = 0;
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
// - preSum[i][j]原因 preSum[i][j + 1] 和 preSum[i + 1][j]都含有preSum[i][j]
preSum[i + 1][j + 1] = preSum[i][j + 1] + preSum[i + 1][j] - preSum[i][j] + matrix[i][j];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
// - preSum[row2 + 1][col1] - preSum[row1][col2 + 1] Because containpreSum[row1][col1]So many lost1个preSum[row1][col1]
return preSum[row2 + 1][col2 + 1] - preSum[row2 + 1][col1] - preSum[row1][col2 + 1] + preSum[row1][col1];
}
}
public static void main(String[] args) {
// 一维前缀和
NumMatrix1 numMatrix1 = new NumMatrix1(new int[][]{
{
3, 0, 1, 4, 2},
{
5, 6, 3, 2, 1},
{
1, 2, 0, 1, 5},
{
4, 1, 0, 1, 7},
{
1, 0, 3, 0, 5}});
// 输出8
System.out.println(numMatrix1.sumRegion(2, 1, 4, 3));
// 二维前缀和
NumMatrix2 numMatrix2 = new NumMatrix2(new int[][]{
{
3, 0, 1, 4, 2},
{
5, 6, 3, 2, 1},
{
1, 2, 0, 1, 5},
{
4, 1, 0, 1, 7},
{
1, 0, 3, 0, 5}});
// 输出8
System.out.println(numMatrix2.sumRegion(2, 1, 4, 3));
}
}
边栏推荐
猜你喜欢

Mysql索引相关的知识复盘一
Why Metropolis–Hastings Works
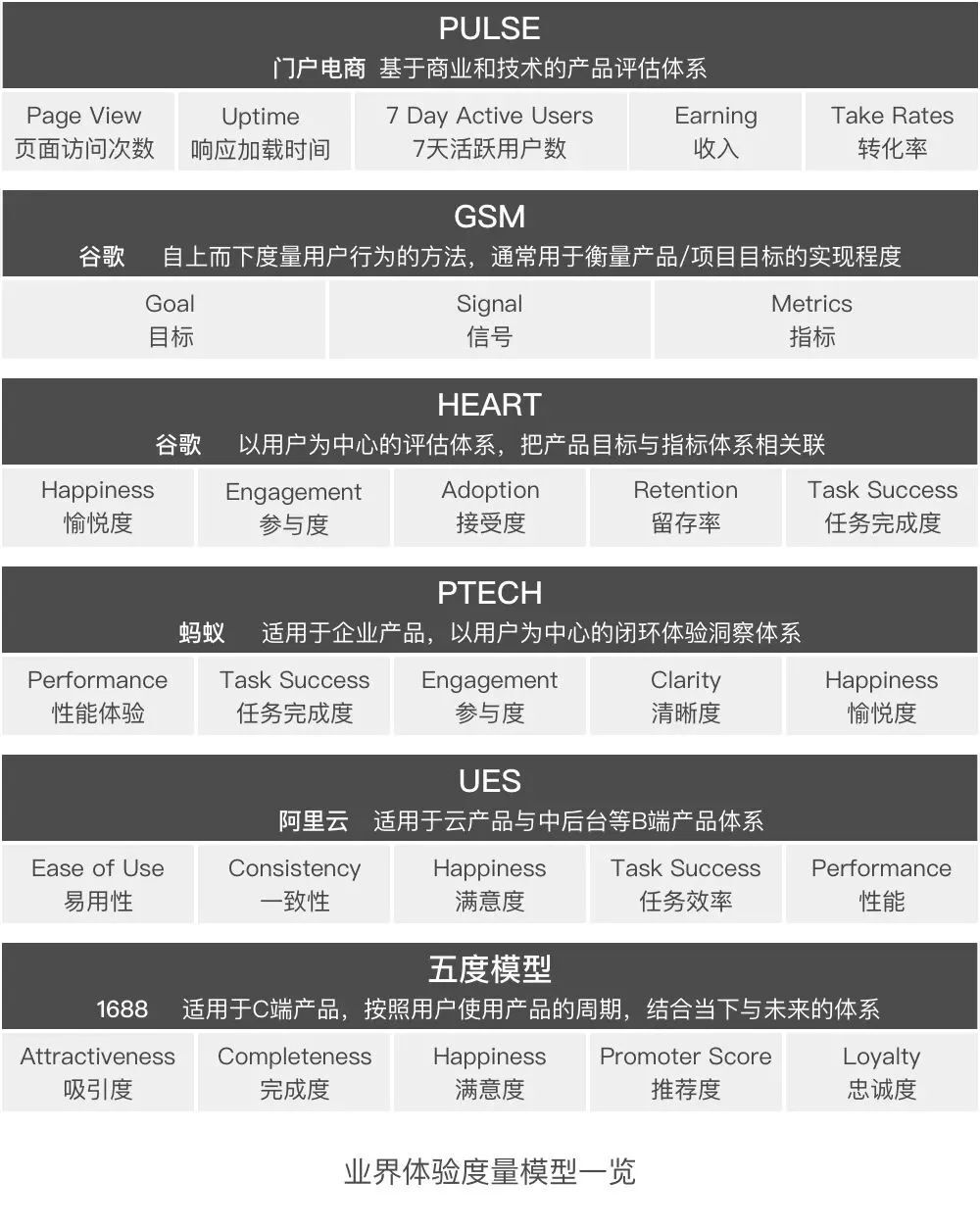
用户体验 | 如何度量用户体验 ?
C#/VB.NET 将PPT或PPTX转换为图像
小程序毕设作品之微信美食菜谱小程序毕业设计成品(2)小程序功能
Mini Program Graduation Works WeChat Food Recipes Mini Program Graduation Design Finished Products (3) Background Functions
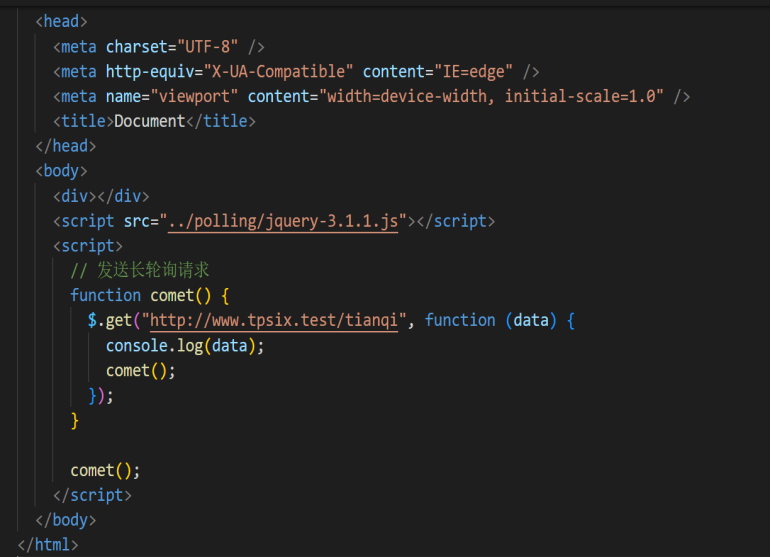
轮询和长轮询的区别

Promise学习(四)异步编程的终极解决方案async + await:用同步的方式去写异步代码

Promise to learn several key questions (3) the Promise - state change, execution sequence and mechanism, multitasking series, abnormal penetration, interrupt the chain of Promise

redis6 跟着b站尚硅谷学习
随机推荐
C语言实现!20000用4秒计算
使用KeyStore生成证书
Google Earth Engine APP——15行代码搞定一个inspector高程监测APP
Promise学习(二)一篇文章带你快速了解Promise中的常用API
OpenHarmony高校技术俱乐部计划发布
C language implementation!20000 in 4 seconds
4种常见的鉴权方式及说明
STM32 personal notes - program run and fly
Glassmorphism design style
Promise学习(三)Promise的几个关键性问题 -- 状态改变、执行顺序与机制、多任务串联、异常穿透、中断promise链
PDMan-domestic free general database modeling tool (minimalist, beautiful)
MacOS下postgresql(pgsql)数据库密码为什么不需要填写或可以乱填写
博弈论(Depu)与孙子兵法(42/100)
小程序毕设作品之微信美食菜谱小程序毕业设计成品(3)后台功能
Guangyu Mingdao was selected into the list of pilot demonstration projects for the development of digital economy industry in Chongqing in 2022
从零开始Blazor Server(4)--登录系统
redis6 跟着b站尚硅谷学习
爱可可AI前沿推介(8.1)
小程序毕设作品之微信美食菜谱小程序毕业设计成品(2)小程序功能
.NET深入解析LINQ框架(三:LINQ优雅的前奏)