当前位置:网站首页>Doing Homework HDU - 1074
Doing Homework HDU - 1074
2022-08-04 10:47:00 【beyond+myself】
題目链接
题意:
1:每次给n个作业及其花费时间和截至时间
2:每次做一个作业直到做完才可以换下一个作业
3:对于每一个作业,每超过一天就会减去1分
4:问减去的最小的分数
5:题中的输入顺序是按字典序的,此链接题目没有说,但是在原题目中是有的,可以到原网站看看
题解:本来想的是dfs,觉得数也不大,剪剪枝就能卡过去,但是T了,后来想了想背包,直接不行,因为这里每件物品都要选择。
最后想到了状压dp,其实状态压缩呢就是将所有事件的状态用0、1两个数字表示,但是我们这样暴力的话还是和dfs一样会超时的。所以状态压缩的关键环节就是寻找状态之间的联系,来去除不需要的状态。
这里我们的主要问题无非就是顺序的问题,这样的情况下,我们假设当前的状态是0010,那么我们枚举第0~n-1的物品,这样在枚举的时候就是枚举下一个状态的过程,这样就可以找到下一个状态,这样我们就可以用当前的状态更新所有0010可以到达的状态。这样我们将所有的状态都枚举出来,最优的答案也就出来了,当然这里记录路径的时候有一个小技巧,我们可以再在dp中记录前一个pre最后递归即可,具体见代码:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
struct node
{
string name;
int d,c;
} a[20];
struct node1
{
int all,day;
int pre;
string name;
} dp[1<<15];//不知道这题为什么在这里卡内存,1<<20会MLE的
void print(int now)
{
if(!now) return;
print(dp[now].pre);
cout<<dp[now].name<<endl;
}
int main()
{
int n,t;
cin>>t;
while(t--)
{
cin>>n;
for(int i=0; i<n; i++)
cin>>a[i].name>>a[i].d>>a[i].c;
for(int i=0; i<1<<n; i++) dp[i].all=0x3f3f3f3f;
dp[0].all=dp[0].day=dp[0].pre=0;
for(int i=0; i<1<<n; i++) //枚举所有的情况
{
for(int j=0; j<n; j++)
{
if((i&(1<<j))==0)
{
int ne=i|(1<<j);
int sco=max(0,dp[i].day+a[j].c-a[j].d);
if(dp[ne].all>dp[i].all+sco)
{
dp[ne].all=dp[i].all+sco;
dp[ne].day=dp[i].day+a[j].c;
dp[ne].pre=i;
dp[ne].name=a[j].name;
}
}
}
}
cout<<dp[(1<<n)-1].all<<endl;
print((1<<n)-1);
}
return 0;
}
注:我们细分析一下,其实这里在更新最小的值的时候其实和那个最短路类似,将当前状态下所有可以到达的状况全部更新。
我们可以简单看一下这个状压dp是如何优化暴力的,暴力的情况下,我们的时间复杂度是n!主要的复杂度在于就是枚举顺序这一环节,我需要知道每种顺序的值,这样才能知道最终状态的值。而状态压缩dp的顺序就是通过当前状态去枚举下面所有的状态,这里dp的好处就是只保留了每种状态下的最小值进而去更新之后状态的值,最终就可以找到最小值,所有dp就是通过递推来优化了暴力。
下面是用dfs写的超时代码:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
const int N=20;
int n;
int ans=0x3f3f3f3f;
vector<string> res;
vector<string> vec;
bool st[N];
struct node
{
string name;
int spend,endd;
bool operator <(node &w)
{
return spend-endd<w.spend-w.endd;
}
}a[N];
void dp(int u,int spend,int now)
{
if(spend>ans) return;//剪枝
if(u>=n)//完成情况
{
bool flag=false;
for(int i=0;i<vec.size()&&i<res.size();i++)
{
if(vec[i]>res[i]) break;
else if(vec[i]<res[i])
{
flag=true;
break;
}
}
if(ans>spend) flag=true;
if(ans<spend) return;
if(flag==true)
{
res.clear();
for(int i=0;i<vec.size();i++)
{
res.push_back(vec[i]);
}
}
ans=spend;
return;
}
for(int i=1;i<=n;i++)
{
if(!st[i])
{
st[i]=true;
vec.push_back(a[i].name);
dp(u+1,spend+max(now+a[i].spend-a[i].endd,0),now+a[i].spend);//这里不能自增,因为会影响u在本次递归的值
st[i]=false;
vec.pop_back();
}
}
}
int main()
{
int t;
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>t;
while(t--)
{
res.clear();
vec.clear();
ans=0x3f3f3f3f;
cin>>n;
for(int i=1;i<=n;i++) st[i]=false;
for(int i=1;i<=n;i++)
{
cin>>a[i].name>>a[i].endd>>a[i].spend;
}
sort(a+1,a+1+n);
dp(0,0,0);
cout<<ans<<endl;
for(int i=0;i<res.size();i++)
{
cout<<res[i]<<endl;
}
}
return 0;
}
我们可以简单的证明一下那个状态压缩是否可以找到最优值:这个状态压缩实际上是从前往后更新的,假设当前是0000,那么可以更新到0001,0010,0100,1000。紧接着我们更新到了0001,也会更新完所有的之后的状态,这样循环正向是可以将所有的状态枚举完全的。而且因为1是不断往后走的,所以当前的状态一定不会枚举到小于他的状态。即当我们暴力到当前状态之后,他不会进行更新,所以就保证了正确性
总结:状态压缩dp是最接近暴力的dp,所有当暴力没法过时,我们应该想想状压dp,而且想的时候一定从最基本的状态想,这样跳跃性不会很大。
边栏推荐
猜你喜欢
随机推荐
Apache Calcite 框架原理入门和生产应用
RAID介绍及RAID5配置实例
datax oracle to oracle离线json文件
八、MFC对话框
safe-point(safepoint 安全点) 和 safe-region(安全区域)「建议收藏」
MATLAB程序设计与应用 3.2 矩阵变换
Heap Sort
无代码平台描述文字入门教程
昨夜梦佳人,七夕试伊妆丨基于ModelArts实现AI妆容迁移丨【玩转华为云】
知其然,知其所以然,JS 对象创建与继承
Rust 入门指南 (用 WASM 开发第一个 Web 页面)
【Inspirational】The importance of review
Super Learning Method
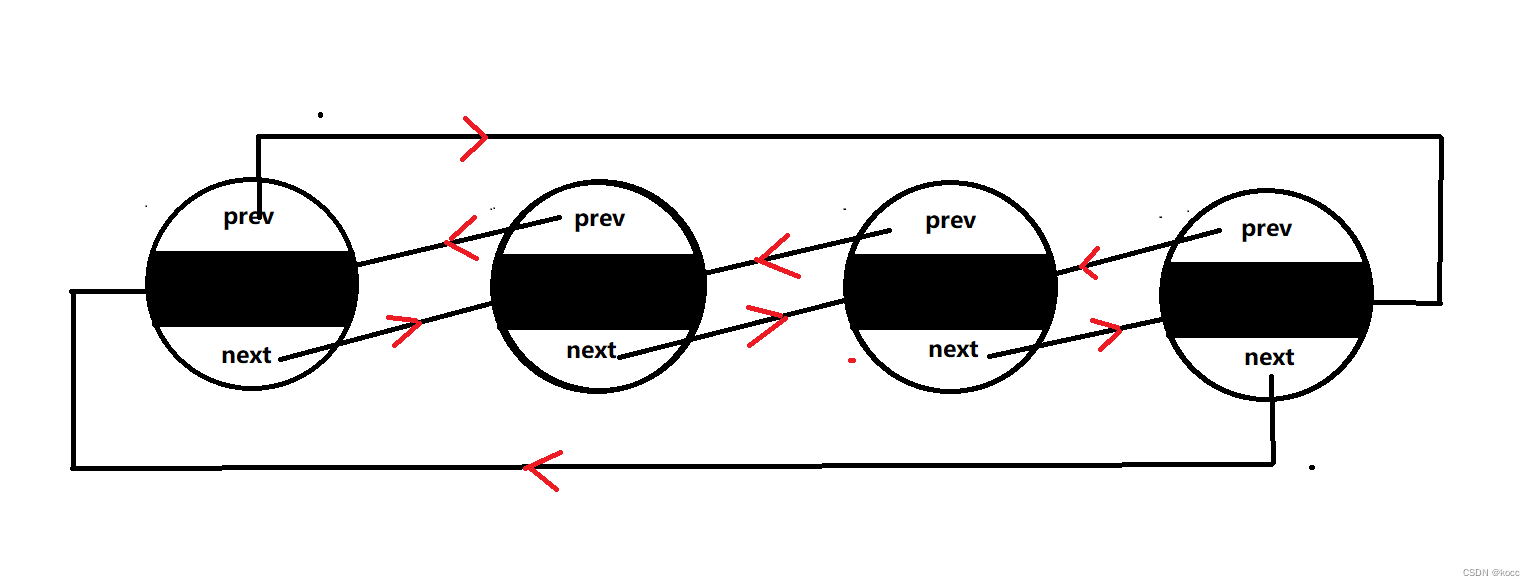
双向带头循环链表实现
什么是终端特权管理
Mobile open source low code tools beeware and kivy
gom登录器配置教程_谷歌浏览器如何使用谷歌搜索引擎
JUC (1) threads and processes, concurrency and parallelism, thread state, locks, producers and consumers
高级转录组分析和R数据可视化火热报名中(2022.10)
Introduction to the core methods of the CompletableFuture interface