当前位置:网站首页>二叉树与堆
二叉树与堆
2022-08-04 09:47:00 【kocc】
文章目录
二叉树与堆
树的概念
概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
有一个特殊的结点,称为根结点,根节点没有前驱结点。除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继。因此,树是递归定义的。
表示
树并不是线性表,因此存储表示起来就比较麻烦,既要保存根节点,也要保存子节点之间的关系,其表示方法也很多,我们常用孩子兄弟表示法:
typedef int DataType;
struct Node
{
struct Node* _firstChild1; // 第一个孩子结点
struct Node* _pNextBrother; // 指向其下一个兄弟结点
DataType _data; // 结点中的数据域
};
仔细看就会发现这个方法很好的将所有的结点全部存储起来: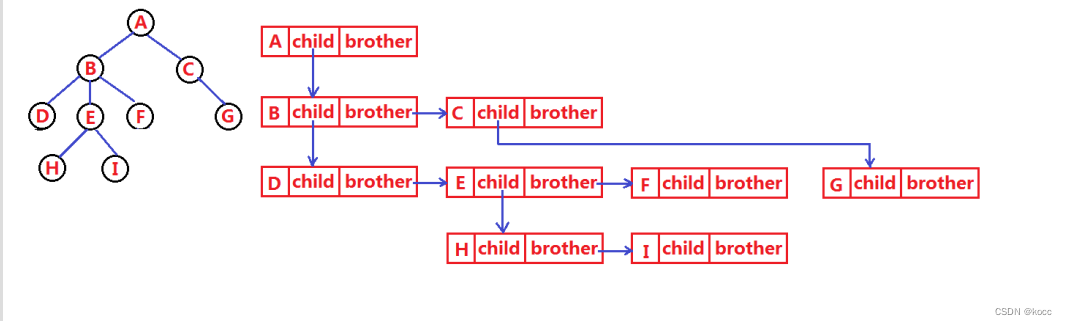
二叉树
概念
二叉树(Binary tree)是n个有限元素的集合,该集合或者为空、或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成,是有序树。当集合为空时,称该二叉树为空二叉树。在二叉树中,一个元素也称作一个节点。
二叉树是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树,且有左右之分。
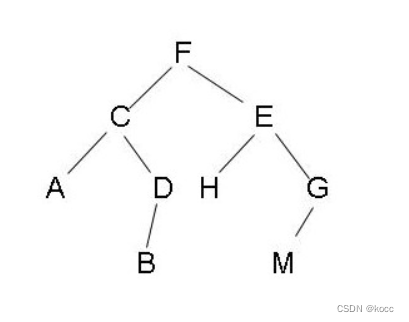
二叉树不存在度大于2的结点,二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
特殊的二叉树
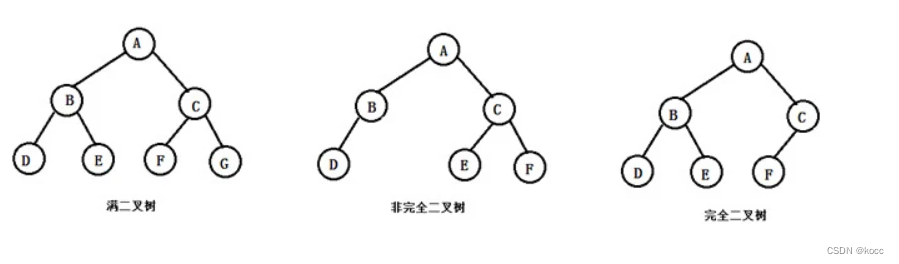
满二叉树
除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树。
由于等比数列的性质,有:
如果一个二叉树的层数为K,且结点总数是2^k-1,则它就是满二叉树。
第i层上的结点数为2^(i-1)
完全二叉树
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。
对于深度为K 的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
二叉树的性质
若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 2^(i-1)个结点.
若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h-1 .
对任何一棵二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为n2 ,则有n0 =n2 +1
若规定根节点的层数为1,具有n个结点的满二叉树的深度h=
log 2 ( n + 1 ) \log_2 (n+1) log2(n+1)
对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对 于序号为i的结点有:
若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
二叉树存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
顺序结构
一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有 堆 才会使用数组来存储,二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
链式结构
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是:链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所 在的链结点的存储地址 。
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{
struct BinTreeNode* _pLeft; // 指向当前节点左孩子
struct BinTreeNode* _pRight; // 指向当前节点右孩子
BTDataType _data; // 当前节点值域
}
堆的概念
如果有一个关键码的集合K = { , , ,…, },把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足: <= 且 <= ( >= 且 >= ) i = 0,1, 2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
(树中的所有父亲均大于等于孩子,即为大根堆)
(树中的所有父亲均小于等于孩子,即为小根堆)
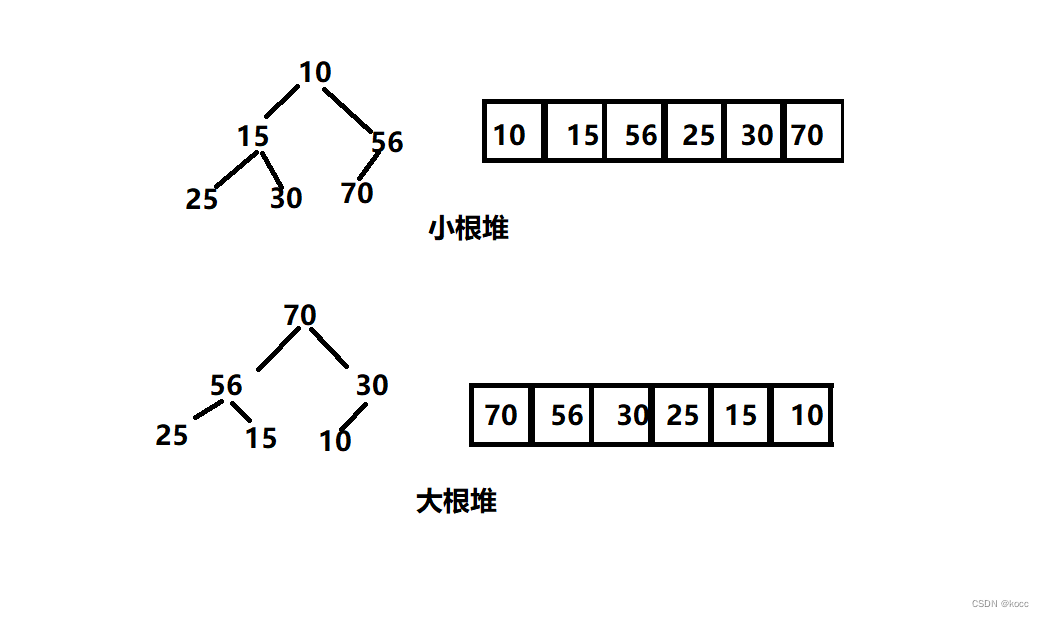
性质:
堆中某个节点的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树。
堆的插入(向上调整算法)
先插入一个数到数组的尾上,再进行向上调整算法,直到满足堆。
void Swap(HeapdataType* a, HeapdataType* b)
{
HeapdataType tmp = *a;
*a = *b;
*b = tmp;
}
void adjustUp(HeapdataType* s, size_t child)
{
size_t parents = (child - 1) / 2;
while (child > 0)
{
if (s[child] < s[parents])//此时以小根堆为标准
{
//交换
Swap(&s[child], &s[parents]);
child = parents;
parents = (child - 1) / 2;
}
else
{
break;
}
}
}
void HeapPush(HP* php, HeapdataType x)
{
//扩容
assert(php);
if (php->size == php->capacity)
{
size_t newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HeapdataType* tmp = (HeapdataType*)realloc(php->s,sizeof(HeapdataType) * newcapacity);
assert(tmp);
php->s = tmp;
php->capacity = newcapacity;
}
//尾插向上调整算法最优,影响最小 效率最高
//先尾插
php->s[php->size] = x;
php->size++;
//向上调整算法
adjustUp(php->s,php->size-1);
}
堆的删除(向下调整算法)
删除堆是删除堆顶的数据(如果是小根堆,即删除最小的元素),将堆顶的数据根最后一个数据交换,然后删除数组最后一个数据,再进行向下调整算法。
void AdjustDown(HPDataType* a, size_t size, size_t root)//需要数组的大小作为参数
{
size_t parent = root;
size_t child = parent * 2 + 1;
while (child < size)//还是小堆
{
// 1、选出左右孩子中小的那个
if (child + 1 < size && a[child+1] > a[child])//判断一下右孩子是否会有越界的风险,必须得判断右孩子存在
{
++child;
}
// 2、如果孩子小于父亲,则交换,并继续往下调整
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}//与向上调整大致思路差不多
else
{
break;
}
}
}
// 删除堆顶的数据。(最小/最大)
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);
Swap(&php->s[0], &php->s[php->size - 1]);
--php->size;
AdjustDown(php->a, php->size, 0);
}
堆排序
建一个小根堆直接将数据插入堆,需要提前写好一个堆进行插入
时间复杂度:O(N*logN)
空间复杂度:O(N)
void HeapSort(int* a, int size)
{
HP hp;
HeapInit(&hp);
for (int i = 0; i < size; ++i)
{
HeapPush(&hp, a[i]);//每次插入自动调整
}
size_t j = 0;
while (!HeapEmpty(&hp))
{
a[j] = HeapTop(&hp);//取到堆顶的元素
j++;
HeapPop(&hp);//将堆顶的元素删除
}
HeapDestroy(&hp);
}
优化
不再借助我们之前写好的堆数据结构,直接建堆进行排序,分为两个步骤,建堆,利用堆删除的原理排序
即建好一个堆,交换顶端与最后一个结点的数,再建一个除最后一个数字的堆,然后再交换,再建,直至排序完成
两种方法:
1.使用向上调整插入数据建堆(效率低) 建堆时间复杂度O(N*logN)
void HeapSort(int* a, int size)
{
for (int i = 1; i < n; ++i)
{
AdjustUp(a, i);
}
}
2.向下调整:建堆时间复杂度O(N),整个排序复杂度为O(N*logN),空间复杂度O(1),优秀高效
void HeapSort(int* a, int n)
{
// 先把所有子树变成堆
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
//n-1代表最后一个叶子结点,((n-1)-1)/2是求父亲结点的公式
{
AdjustDown(a, n, i);
}
size_t end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}
升序—建大堆
降序—建小堆
如果升序建小堆的话,最小的数已经在堆顶了,剩下的数字关系全是乱的,需要重新建堆,而建堆最快也要O(N)。
可以是可以,但是效率低下而且比较复杂,因此我们利用建大堆,降序同理建小堆
应用—TopK问题
从n个未排序的数中得到的最大(最小)的K个数,称为TopK问题。
我们首先的想法是将这n个数建堆,删除K次就可以选出想要的数,但是这种方法有缺陷,如果n非常非常大,远大于K时,该方法就不可以用了,因为内存放不下这么多的数据,所以我们优化:
若要找最大的前K个,我们建立一个K个数的小堆,然后剩下的N-K个数依次遍历,如果比堆顶的数据大,就替换进堆,最后堆里面的K个数就是最大的K个。
时间复杂度:O(K+logK*(N-K))
空间复杂度:O(K)
void PrintTopK(int* a, int n, int k)
{
// 1. 建堆--用a中前k个元素建堆
int* kminHeap = (int*)malloc(sizeof(int)*k);
assert(kminHeap);
for (int i = 0; i < k; ++i)
{
kminHeap[i] = a[i];
}
// 建小堆
for (int j = (k - 1 - 1) / 2; j >= 0; --j)
{
AdjustDown(kminHeap, k, j);
}
// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换
for (int i = k; i < n; ++i)
{
if (a[i] > kminHeap[0])
{
kminHeap[0] = a[i];
AdjustDown(kminHeap, k, 0);
}
}
for (int j = 0; j < k; ++j)
{
printf("%d ", kminHeap[j]);
}
printf("\n");
free(kminHeap);
}
二叉树链式结构
二叉树可以分为三部分:根、左子树、右子树,它的这三部分又可以分为根、左子树、右子树,因此我们在学习时要有递归的思维
二叉树的遍历
现有一颗二叉树: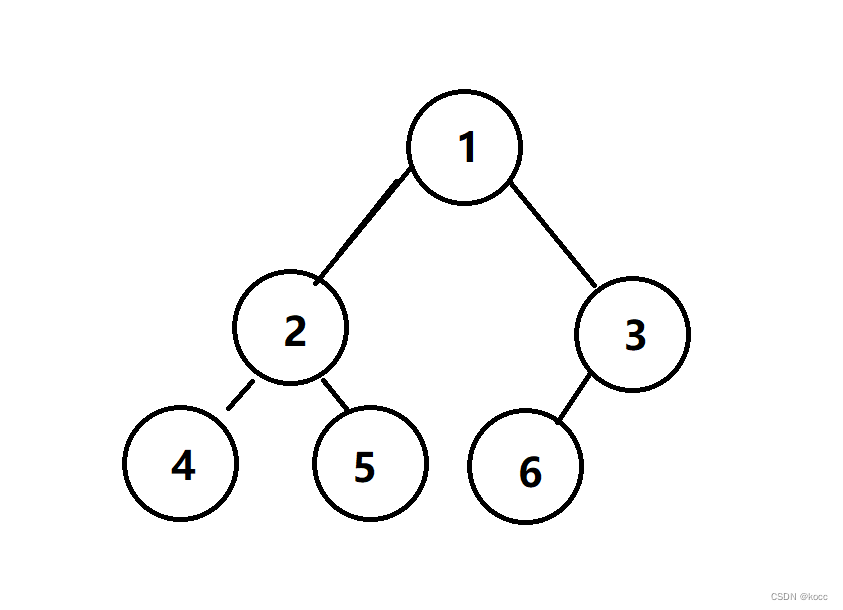
其遍历可以分为前中后序以及层序,区别就在于根、左子树、右子树的先后顺序
前序遍历:
访问根结点的操作发生在遍历其左右子树之前。
遍历结果:1 2 4 NULL NULL 5 NULL NULL 3 6 NULL NULL NULL
void PrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
中序遍历:
访问根结点的操作发生在遍历其左右子树之中(间)。
遍历结果:NULL 4 NULL 2 NULL 5 NULL 1 NULL 6 NULL 3 NULL
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
后续遍历:
访问根结点的操作发生在遍历其左右子树之后。
遍历结果:NULL NULL 4 NULL NULL 5 2 NULL NULL 6 NULL 3 1
void PostorderOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostorderOrder(root->left);
PostorderOrder(root->right);
printf("%d ", root->data);
}
**层序遍历:**层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层 上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历
遍历结果: 1 2 3 4 5 6
边栏推荐
猜你喜欢
![Could you please talk about how the website is accessed?[Interview questions in the web field]](/img/06/5ecc617edc4131c31f71d5e019a64c.png)
Could you please talk about how the website is accessed?[Interview questions in the web field]

【c】操作符详解(二)
VRRP + MSTP configuration, huawei eNSP experiment 】 【

MindSpore:Ascend运行出现问题
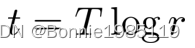
参数优化文档介绍
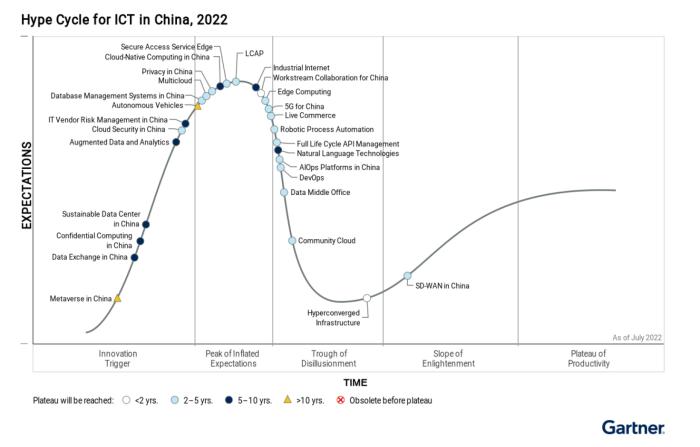
2022 Cloud Native Computing代表厂商 | 灵雀云第三次入选Gartner中国ICT技术成熟度曲线报告
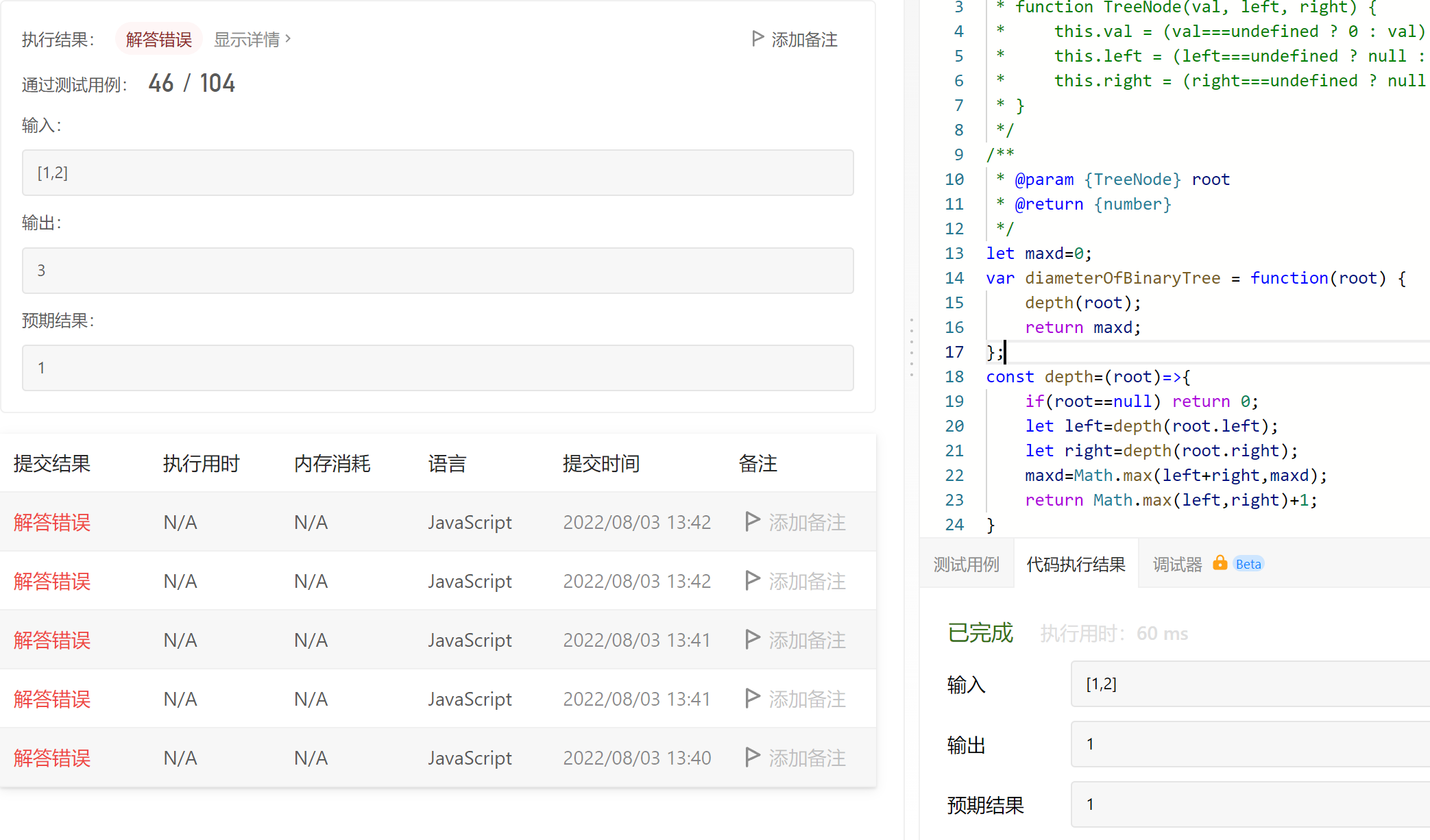
leetcode每天5题-Day06
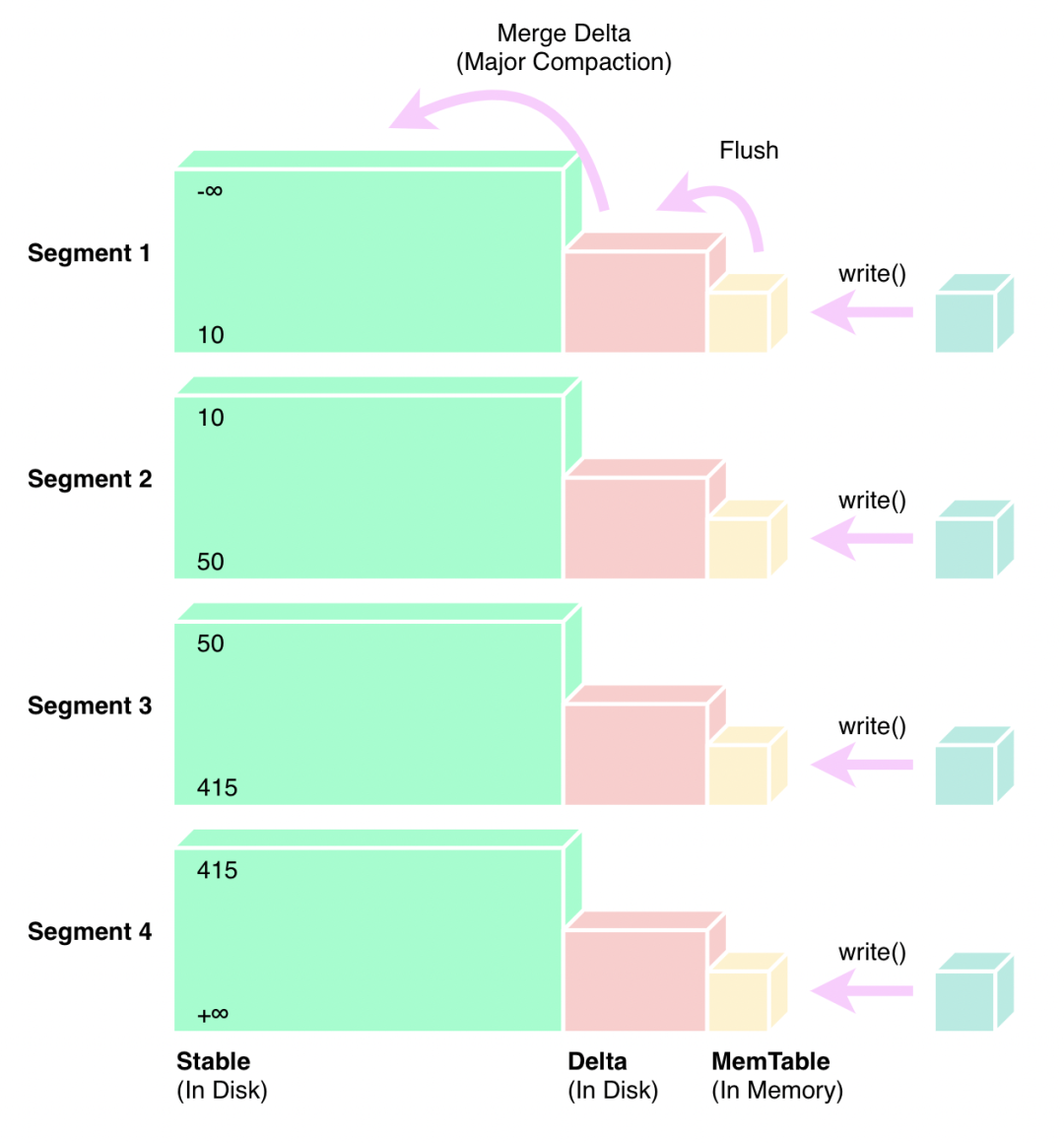
TiFlash 源码阅读(五) DeltaTree 存储引擎设计及实现分析 - Part 2
双重for循环案例以及while循环和do while循环案例

MindSpore:【model_zoo】【resnet】尝试用THOR优化器运行时报cannot import name ‘THOR‘
随机推荐
After four years of outsourcing, the autumn recruits finally landed
How Oracle for current library or certain library data on the same server number?
DOM简述
leetcode动态规划系列(求路径篇)
XCTF-easy_Maze
暴力破解-破解 Apache BASIC 认证
MindSpore:【model_zoo】【resnet】尝试用THOR优化器运行时报cannot import name ‘THOR‘
GBsae 8c 数据库使用中报错,肿么办?
HTB-Nibbles
LeetCode中等题之设计循环队列
冰蝎逆向初探
leetcode二叉树系列(二叉搜索树篇)
多了&lt;audio controls=
多媒体和物联网技术让版本“活”起来 129张黑胶唱片“百年留声”
Person.class.getInterfaces() 注意使用方法
leetcode动态规划经典例题——53.最大子数组和
Producer and Consumer Problems in Concurrent Programming
Win11如何隐藏输入法悬浮窗?
Since his 97, I roll but he...
云函数实现网站自动化签到配置详解【Web函数/Nodejs/cookie】