当前位置:网站首页>数学建模学习(76):多目标线性规划模型(理想法、线性加权法、最大最小法),模型敏感性分析
数学建模学习(76):多目标线性规划模型(理想法、线性加权法、最大最小法),模型敏感性分析
2022-08-02 03:37:00 【川川菜鸟】
一、多目标线性规划模型
1.1 定义
多目标线性规划模型是有两个或两个以上的目标函数,且所有的目标函数和约束条件都是线性的。其数学模型表示为:

摘自百度百科:
https://baike.baidu.com/item/%E5%A4%9A%E7%9B%AE%E6%A0%87%E7%BA%BF%E6%80%A7%E8%A7%84%E5%88%92/19134131
1.2 相关函数使用方法
常用的求解最优化问题的函数,有线性规划问题的linprog,非线性规划问题的fmincon,最大最小问题的fminimax,求解多目标的fgoalattain等
线性规划问题函数:
寻找约束非线性多变量函数的最小值: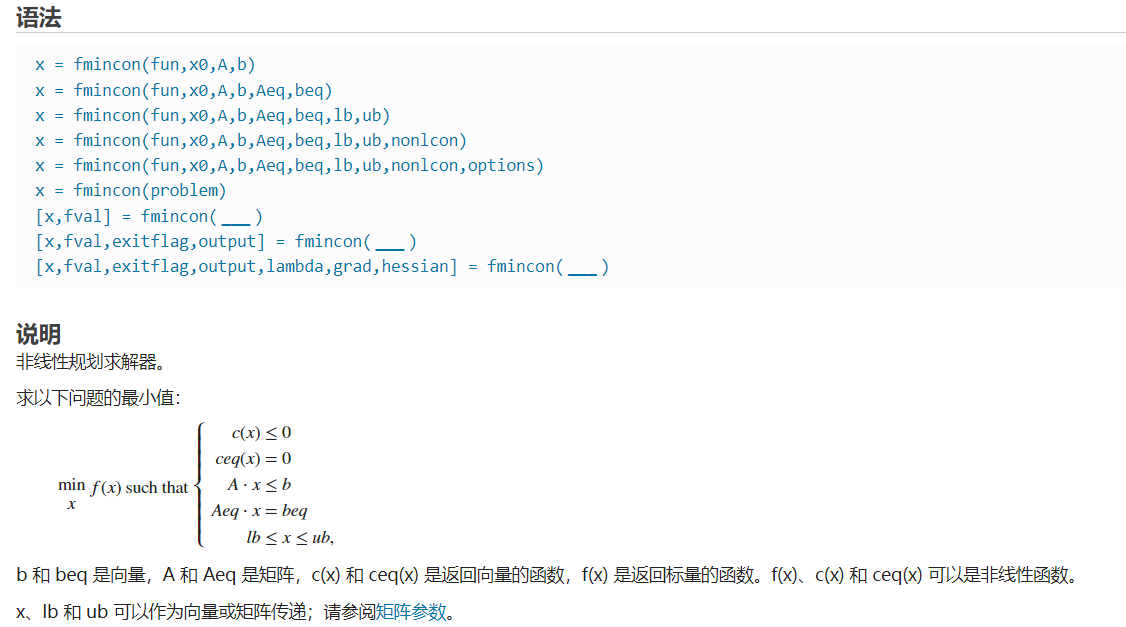
求解涉及多目标的目标达到问题fgoalattain:
1.3 求解方法
多目标线性规划是多目标最优化理论的重要组成部分,由于多个目标之间的矛盾性和不可公度性,要求使所有目标均达到最优解是不可能的,因此多目标规划问题往往只是求其有效解(非劣解)。目前求解多目标线性规划问题有效解的方法,有理想点法、线性加权和法、最大最小法、目标规划法,模糊数学解法等。为了求得多目标规划问题的非劣解,常常需要将多目标规划问题转化为单目标规划问题去处理。实现这种转化,有如下几种建模方法:
效用最优化模型(线性加权法):线性加权和法(linear weighted sum method)是一种评价函数方法,是按各目标的重要性赋予它相应的权系数,然后对其线性组合进行寻优的求解多目标规划问题的方法。
罚款模型(理想点法):规划决策者对每一个目标函数都能提出所期望的值(或称满意值);通过比较实际值与期望值之间的偏差来选择问题的解。

约束模型(极大极小法):若规划问题的某一目标可以给出一个可供选择的范围,则该目标就可以作为约束条件而被排除出目标组,进入约束条件组中。假如,除第一个目标外,其余目标都可以提出一个可供选择的范围,则该多目标规划问题就可以转化为单目标规划问题。

目标达到法:先将多目标规划模型化为标准形式,在求解之前,先设计与目标函数相应的一组目标值理想化的期望目标与每一个目标对应的权重系数,再设松弛因子,对多目标规划问题进行转化。
目标规划模型(目标规划法):需要预先确定各个目标的期望值,同时给每一个目标赋予一个优先因子和权系数,假定有K个目标,L个优先级( L≤K),再通过建立目标规划模型进行求解。
摘自百度百科:
https://baike.baidu.com/item/%E5%A4%9A%E7%9B%AE%E6%A0%87%E7%BA%BF%E6%80%A7%E8%A7%84%E5%88%92/19134131
二、理想点法
2.1 问题
多目标规划问题如下:
2.2 求解
2.2.1 第一步
第一步:分别求解目标函数的最值
1)第一个目标函数
clc
clear all
f=[3;-2]; %linprog函数求的是最小值,取反
a=[2 3;2 1];%约束左侧系数
b=[18;10]; %约束右侧系数
lb=[0;0]; %瞎想
ub=[]; %上限
[x,favl]=linprog(f,a,b,[],[],lb,ub);
x
-favl %f取反后就是球的最小值,相反就是最大值
结果如下: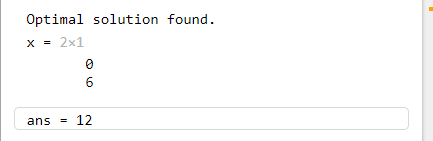
2)同理,第二个目标函数
clc
clear all
f=[-4;-3];
a=[2 3;2 1];
b=[18;10];
lb=[0;0];
ub=[];
[x,favl]=linprog(f,a,b,[],[],lb,ub);
x
-favl
如下:
我们可以看到两个目标函数最大值分别为12和24。因此理想点:(12,24)
2.2.2 第二步
根据以上求解的结果,就变成求解:
代码如下:
clc
clear all
x0=[1;1];%初始点,指定为实数向量或实数数组
a=[2 3;2 1];
b=[18;10];
lb=[0;0];
ub=[];
%多目标函数就是带入两个目标函数开平方
x=fmincon('((-3*x(1)+2*x(2)-12)^2+(4*x(1)+3*x(2)-24)^2)^(1/2)',x0,a,b,[],[],lb,ub);
f1=-3*x(1)+2*x(2)
f2=4*x(1)+3*x(2)
如下:
以上就是f1和f2的最佳值了。
三、线性加权法
我们假设每个目标函数的权重为0.5,带入后得到x1系数为0.5,x2系数为2.5,由于需要取最大值,所以取反为-0.5,-2.5
代码如下:
clc
clear all
%这个系数要不断尝试,因为没有实际场景。实际场景能直接看出权重。
f=[-0.5;-2.5]; %目标函数的系数
a=[2 3;2 1];
b=[18;10];
lb=[0;0];
ub=[];
x=linprog(f,a,b,[],[],lb,ub)
%x为0,6,带入目标函数:f1=12,f2=18
如下: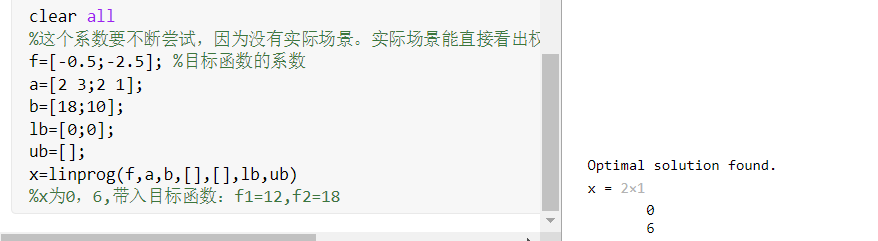
四、最大最小法
4.1 第一步
第一步,编写目标函数mubiao.m:
function f=mubiaot(x)
f(1)=3*x(1)-2*x(2);
f(2)=-4*x(1)-3*x(2);
4.2 第二步
第二步:计算
clc
clear all
x0=[0;0]; %起点设置特殊点0 0
a=[2 3;2 1];
b=[18;10];
lb=[0;0];
[x,favl]=fminimax(@mubiaot,x0,a,b,[],[],lb,[]);
x
-favl %最小值取反就是最大值
如下:
输出结果为:x1=0,x2=6,对应的目标值为f1=12,f2=18
五、线性加权与敏感性分析
5.1 参考
先以这位博主的案例作为分析,原文
https://blog.csdn.net/weixin_54338498/article/details/125996359
题目如下:
利用我们前面学到的线性加权法,很容易写出代码如下:
clc
clear all
%线性加权法
w1 = 0.4; w2 = 0.6; % 两个目标函数的权重 x1 = 5 x2 = 2
c = [w1/30*2+w2/2*0.4 ;w1/30*5+w2/2*0.3] % 线性规划目标函数的系数,就是合并题目中的x1和x2
A = [-1 -1]; b = -7; % 不等式约束
lb = [0 0]'; ub = [5 6]'; % 上下界
[x,fval] = linprog(c,A,b,[],[],lb,ub)
f1 = 2*x(1)+5*x(2)
f2 = 0.4*x(1) + 0.3*x(2)
如下:
敏感性分析就是一点点修改参数查看变化:
clear;clc
W1 = 0.1:0.001:0.5; W2 = 1- W1;
n =length(W1);
F1 = zeros(n,1); F2 = zeros(n,1); X1 = zeros(n,1); X2 = zeros(n,1); FVAL = zeros(n,1);
A = [-1 -1]; b = -7; % 不等式约束
lb = [0 0]; ub = [5 6]; % 上下界
for i = 1:n
w1 = W1(i); w2 = W2(i);
c = [w1/30*2+w2/2*0.4 ;w1/30*5+w2/2*0.3]; % 线性规划目标函数的系数
[x,fval] = linprog(c,A,b,[],[],lb,ub);
F1(i) = 2*x(1)+5*x(2);
F2(i) = 0.4*x(1) + 0.3*x(2);
X1(i) = x(1);
X2(i) = x(2);
FVAL(i) = fval;
end
% 「Matlab」“LaTex字符汇总”讲解:https://blog.csdn.net/Robot_Starscream/article/details/89386748
% 在图上可以加上数据游标,按住Alt加鼠标左键可以设置多个数据游标出来。
figure(1)
plot(W1,F1,W1,F2)
xlabel('f_{1}的权重')
ylabel('f_{1}和f_{2}的取值')
legend('f_{1}','f_{2}')
figure(2)
plot(W1,X1,W1,X2)
xlabel('f_{1}的权重')
ylabel('x_{1}和x_{2}的取值')
legend('x_{1}','x_{2}')
figure(3)
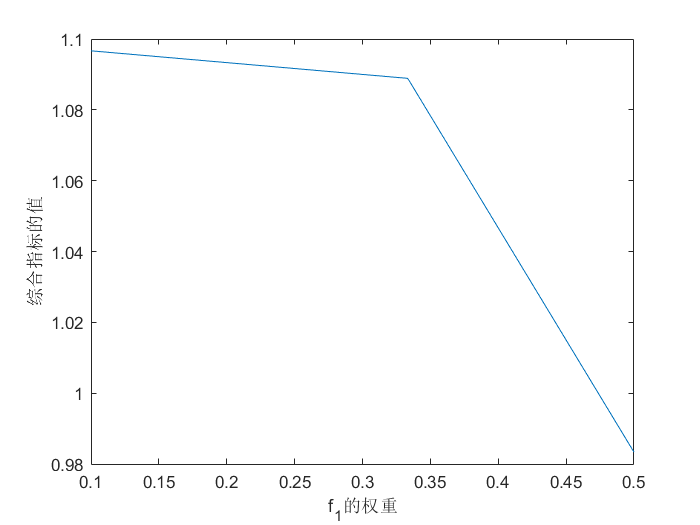
plot(W1,FVAL) % 看起来是两个直线组合起来的下半部分
xlabel('f_{1}的权重')
ylabel('综合指标的值')
如下: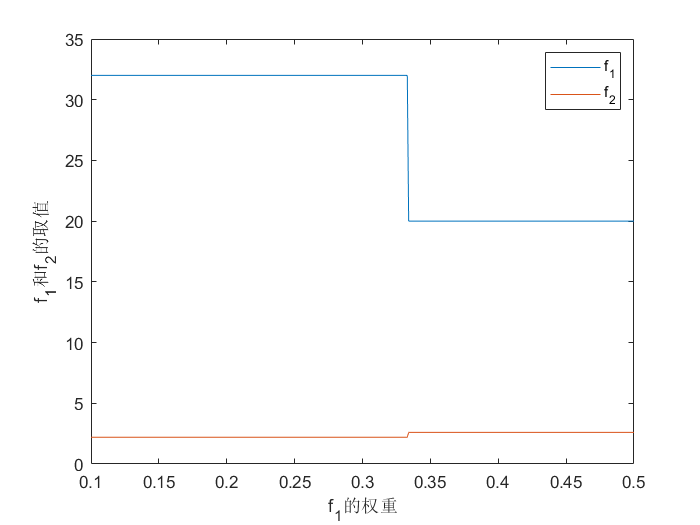

5.2 解题
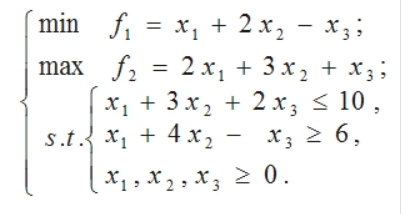
应用到本篇文章中题目,我们只需要修改一些参数即可,不必大量修改,因此当作模板用了。
可修改的参数:W1、A、b、lb、ub、c (这个参数需要根据题意修改,请对比上面参考的题目),具体地方我已在代码中做了注释:
clear;clc
%权重和为1
W1 = 0.1:0.001:0.5; W2 = 1- W1;
n =length(W1);
F1 = zeros(n,1); F2 = zeros(n,1); X1 = zeros(n,1); X2 = zeros(n,1); FVAL = zeros(n,1);
%修改为符合本题目的约束
A = [2 3;2 1]; b = [18;10]; % 不等式约束
lb=[0;0];
ub=[]; % 上下界
for i = 1:n
w1 = W1(i); w2 = W2(i);
%根据具体情况修改
% 这里应该是:w1*f1+w2*f2=(-3w1+4w2)x1+(2w1+3w2)x2,最大值系数取反
c = [-(-3*w1+4*w2) ;-(2*w1+3*w2)]; % 线性规划目标函数的系数
[x,fval] = linprog(c,A,b,[],[],lb,ub);
%修改目标函数
F1(i) = -3*x(1)+2*x(2);
F2(i) = 4*x(1) + 3*x(2);
X1(i) = x(1);
X2(i) = x(2);
FVAL(i) = fval;
end
figure(1)
plot(W1,F1,W1,F2)
xlabel('f_{1}的权重')
ylabel('f_{1}和f_{2}的取值')
legend('f_{1}','f_{2}')
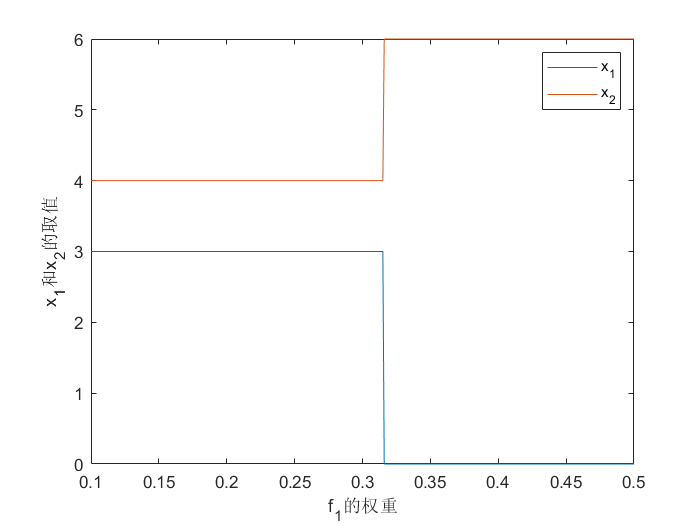
figure(2)
plot(W1,X1,W1,X2)
xlabel('f_{1}的权重')
ylabel('x_{1}和x_{2}的取值')
legend('x_{1}','x_{2}')
figure(3)
plot(W1,FVAL) % 看起来是两个直线组合起来的下半部分
xlabel('f_{1}的权重')
ylabel('综合指标的值')
如下: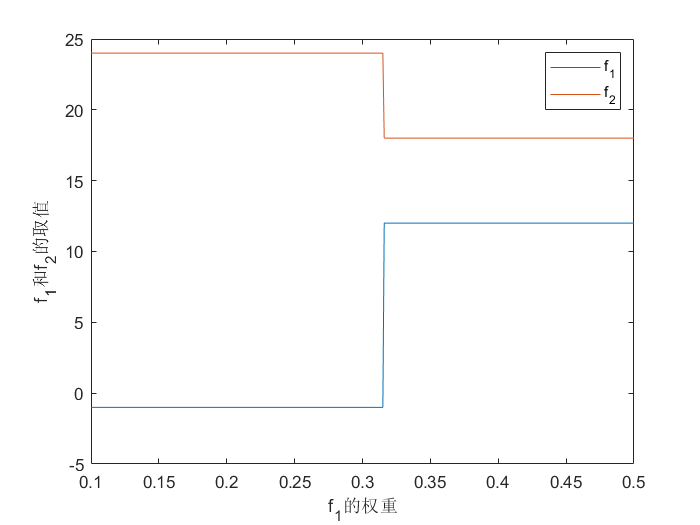
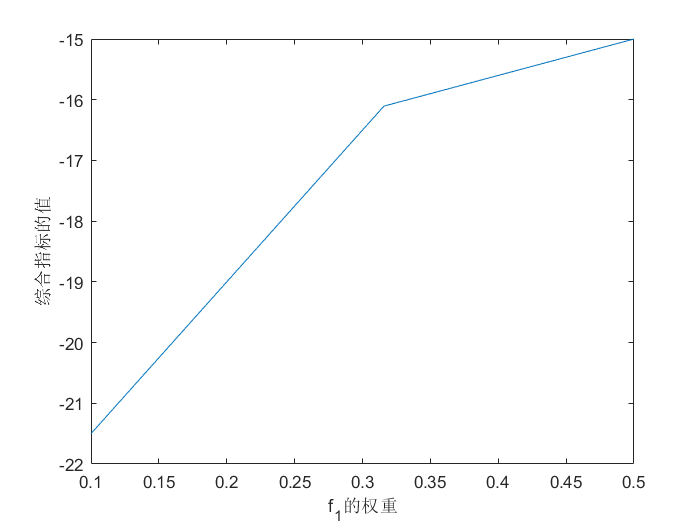
六、总结
以上介绍了三种方法的使用,综合这三种方法:理想点法和最大最小法效果应该一样;线性加权法需要设定权重,这个应该要根据应用场景来对目标函数进行权重设置,注意权重和为1。
如有不理解,可以v咨询:
sprintf('我的v:hxgsrubxjogxeeag')
如下:
这篇教程我用了很久时间来编写,同时也参考了一些文献,引用网址在具体地方已注明。希望这篇教程能够帮助你轻松学会多目标规划的求解。
边栏推荐
猜你喜欢
![[Win11] PowerShell cannot activate Conda virtual environment](/img/53/464ffb5ef80ce8f6ee19e9ea96c159.png)
[Win11] PowerShell cannot activate Conda virtual environment

吴恩达机器学习系列课程笔记——第十三章:聚类(Clustering)
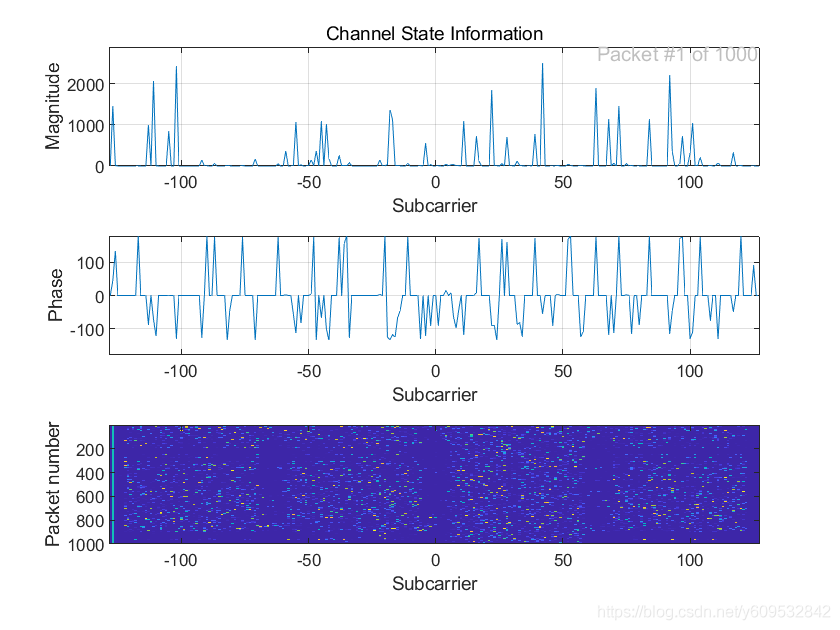
Nexus 5手机使用Nexmon工具获取CSI信息
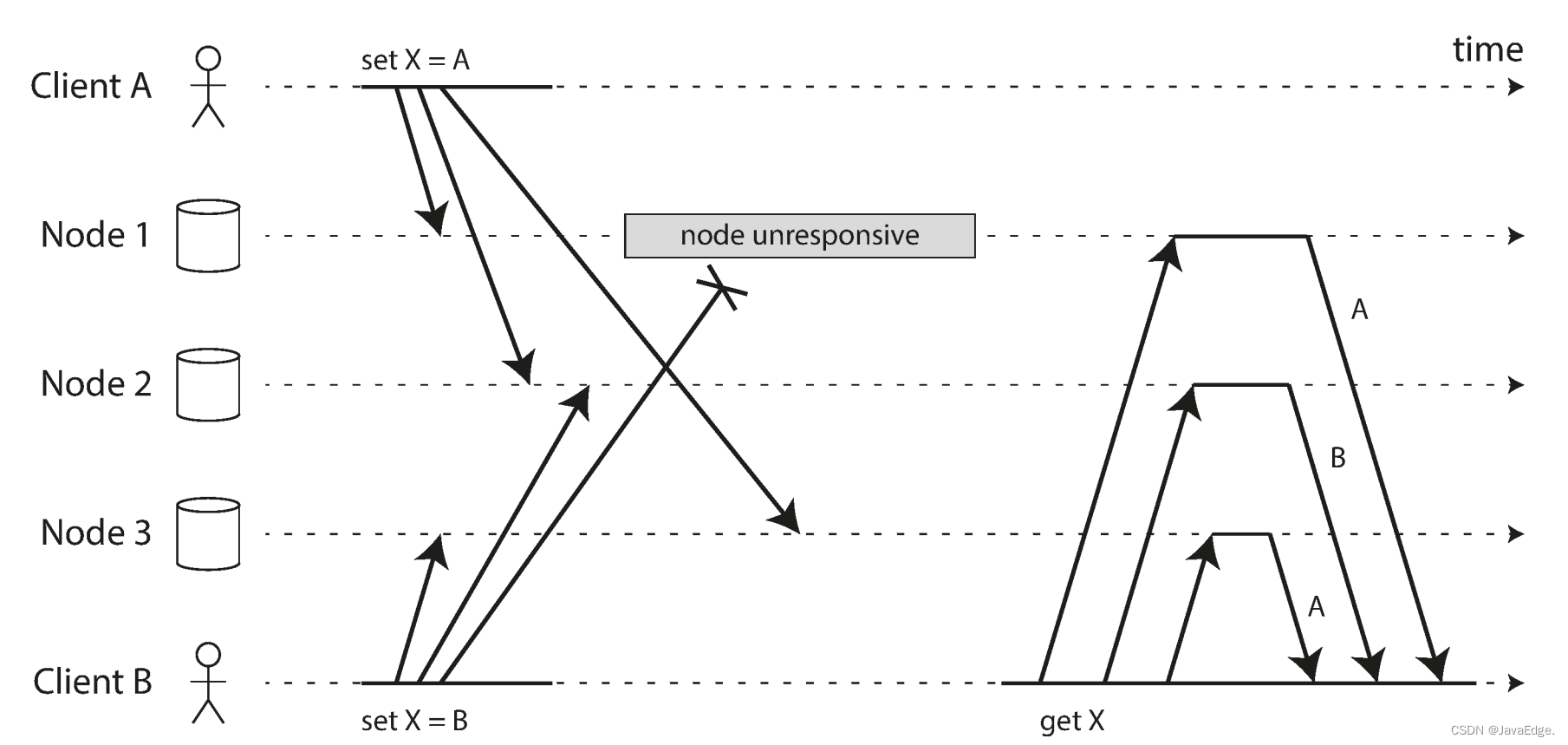
多数据中心操作和检测并发写入

Research Notes (8) Deep Learning and Its Application in WiFi Human Perception (Part 1)
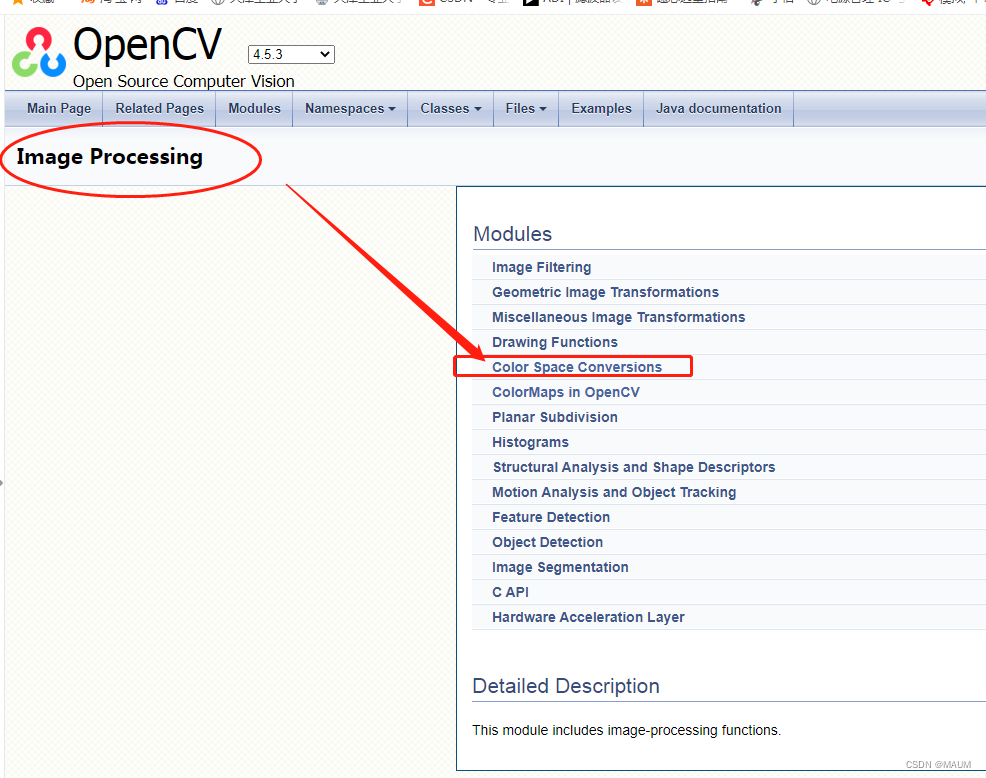
QT中更换OPENCV版本(3->4),以及一些宏定义的改变
迭代器与生成器

flasgger手写phpwind接口文档
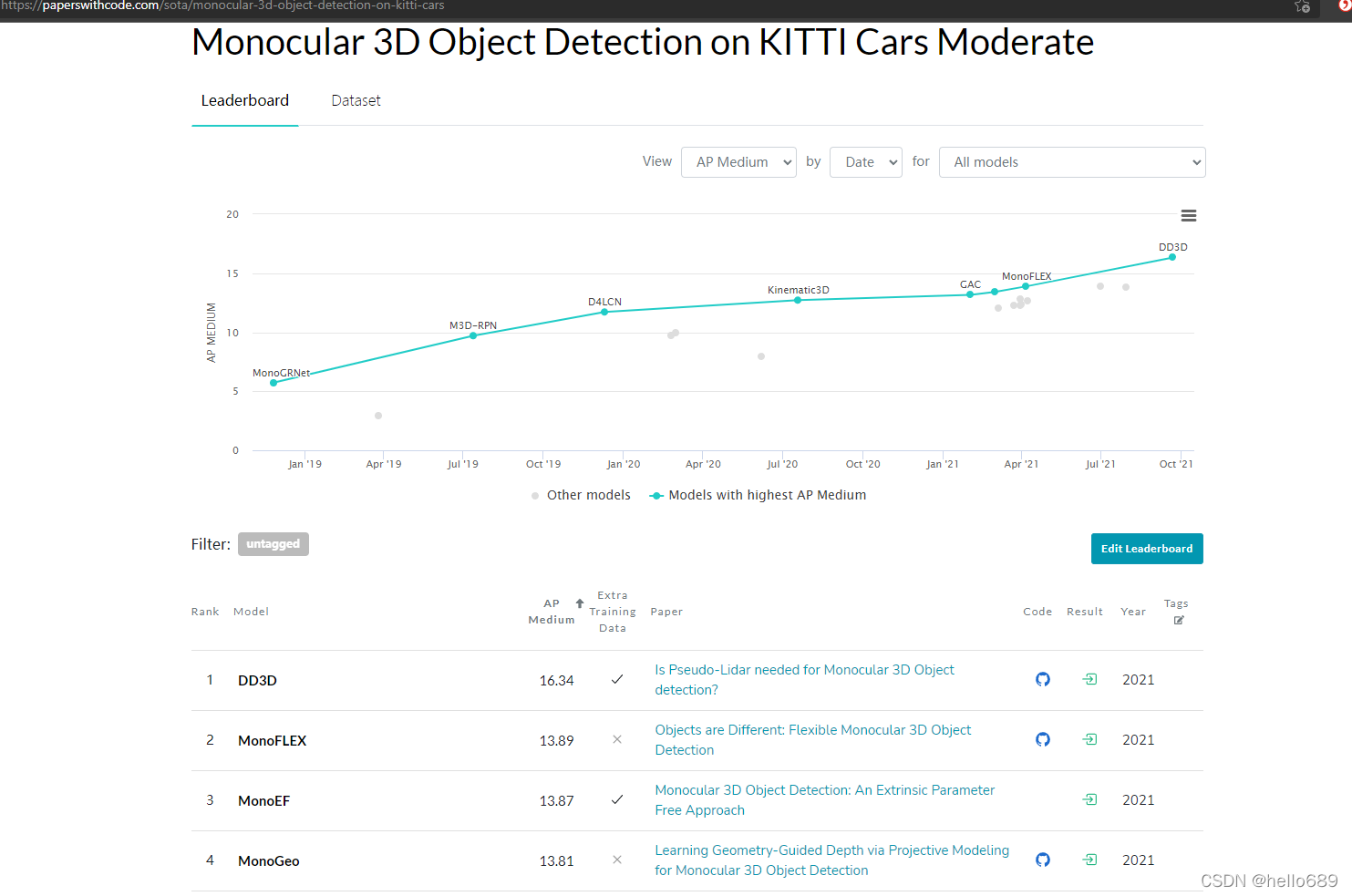
单目3D目标检测之入门

腾讯云+keepalived搭建云服务器主备实践
随机推荐
Deep Blue Academy - Visual SLAM Lecture Fourteen - Chapter 5 Homework
科研笔记(八) 深度学习及其在 WiFi 人体感知中的应用(下)
未来智安创始人兼CEO唐伽佳荣膺36氪X·36Under36 “S级创业者”
复制延迟案例(4)-一致前缀读
科研笔记(六) 基于环境感知的室内路径规划方法
BCS演讲实录 | 未来智安CTO陈毓端精讲《XDR扩展威胁检测响应探索与实践》
剩余参数、数组对象的方法和字符串扩展的方法
3D目标检测之数据集
拦截器Sercurity权限管理和加密方式的登录认证使用
WIN10什么都没开内存占用率过高, WIN7单网卡设置双IP
基于sysbench工具的压力测试---MyCat2.0+MySql架构
PHP将字符切割成每个拼音
MapFi论文架构整理
多主复制下处理写冲突(3)-收敛至一致的状态及自定义冲突解决逻辑
深蓝学院-视觉SLAM十四讲-第五章作业
flask简单接口实现
SCI期刊最权威的信息查询步骤!
jmeter之数据库连接JDBC安装与使用
CaDDN代码调试
Excel操作技巧大全