当前位置:网站首页>Chapter8 Support Vector Machines
Chapter8 Support Vector Machines
2022-07-30 04:29:00 【Sang Zhiwei 0208】
1 理解支持向量机SVM的原理和目标(what)
1.1 原理
SVMThe rationale is to find a linear classifier that maximizes the separation hyperplane in the feature space.
- When the training samples are linearly separable,通过硬间隔最大化,学习一个线性分类器,即线性可分支持向量机.
- When the training data is approximately linearly separable,Slack variables can be introduced,通过软间隔最大化,学习一个线性分类器,即线性支持向量机.
- When the training data is linearly inseparable,通过核函数以及软间隔最大化,Learn about fractional linear support vector machines.
1.2 目标
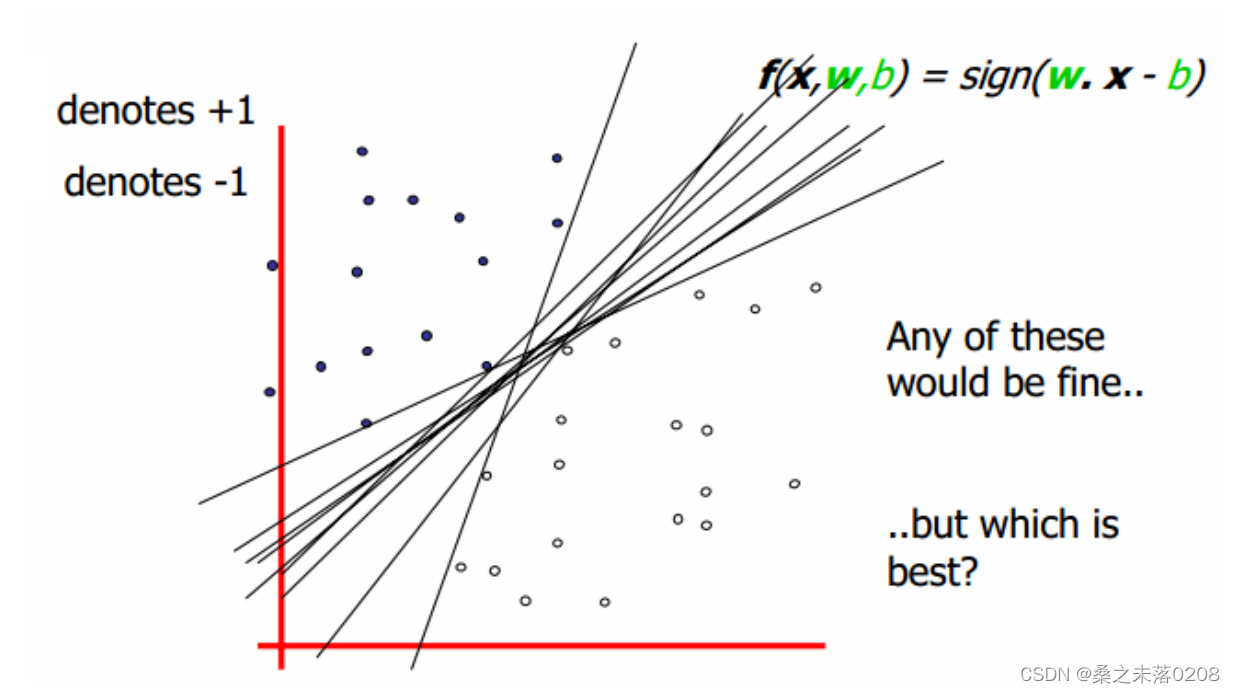
Find infinite linear functions of all sample distancesf(x,w,b)最小的距离,Find the line with the largest distance among these distances,即求取w,b的值
如图所示: ,其中
,其中 代表向量.
代表向量.
The sample distance is the distance between this function:
所以目标为:
2 掌握支持向量机的计算过程和算法步骤(how)
2.1 计算过程
假设给定一个特征空间上的训练数据集 ,其中
,其中 ;
;
 表示为第i个实例(若n大于1,则
表示为第i个实例(若n大于1,则 为向量);
为向量);
 为
为 的类标记,即当
的类标记,即当 时,
时, 为正例,当
为正例,当 时
时 为负例.
为负例.
 称为样本点.
称为样本点.
给定线性可分训练数据集,The separating hyperplane obtained by maximizing the interval is  ,相应的分类决策函数
,相应的分类决策函数 ,该决策函数称为线性可分支持向量机.
,该决策函数称为线性可分支持向量机.
 是某个确定的特征空间转换函数,它的作用是将x映射到(最高的)维度.
是某个确定的特征空间转换函数,它的作用是将x映射到(最高的)维度.
Solve the separating hyperplane problem=Solve the corresponding convex quadratic programming problem.
(1)根据题设 ,有当
,有当 ,
,
从而 .【
.【 为预测值
为预测值  为真实值】
为真实值】
change by a certain percentagew,b(The position of the hyperplane does not change at this time,But the function interval can be changed),则t*yThe value also changes,从而:
 ,其中
,其中 为
为 的
的 范数.
范数.
目标函数:![\underset{w,b}{argmax}\left \{ \frac{1}{||w||}\underset{i}{min} [y_{i}\cdot (w^{T}\cdot \Phi (x_{i})+b)]\right \}](http://img.inotgo.com/imagesLocal/202207/30/202207300416099824_39.gif)
(2)(If the geometric distance is B,即 (B为常数)
(B为常数)

Divide both sides of the equation byB:
 ,At this point the geometric distance becomes 1.
,At this point the geometric distance becomes 1.

通过等比例缩放w的方法,The function values of these two types of points are satisfied ,即约束条件.
,即约束条件.

(3)So the original problem can be transformed into the following problem:
约束条件——
原目标函数——![\underset{w,b}{argmax}\left \{ \frac{1}{||w||}\underset{i}{min} [y_{i}\cdot (w^{T}\cdot \Phi (x_{i})+b)]\right \}](http://img.inotgo.com/imagesLocal/202207/30/202207300416099824_39.gif)
新目标函数—— ,即
,即 ,即
,即
(4)所用方法:拉格朗日乘子法
设函数
原问题是极小极大问题:
The dual problem of the primal problem is the minimax problem:
然后分别对 求偏导,令其为0:
求偏导,令其为0:


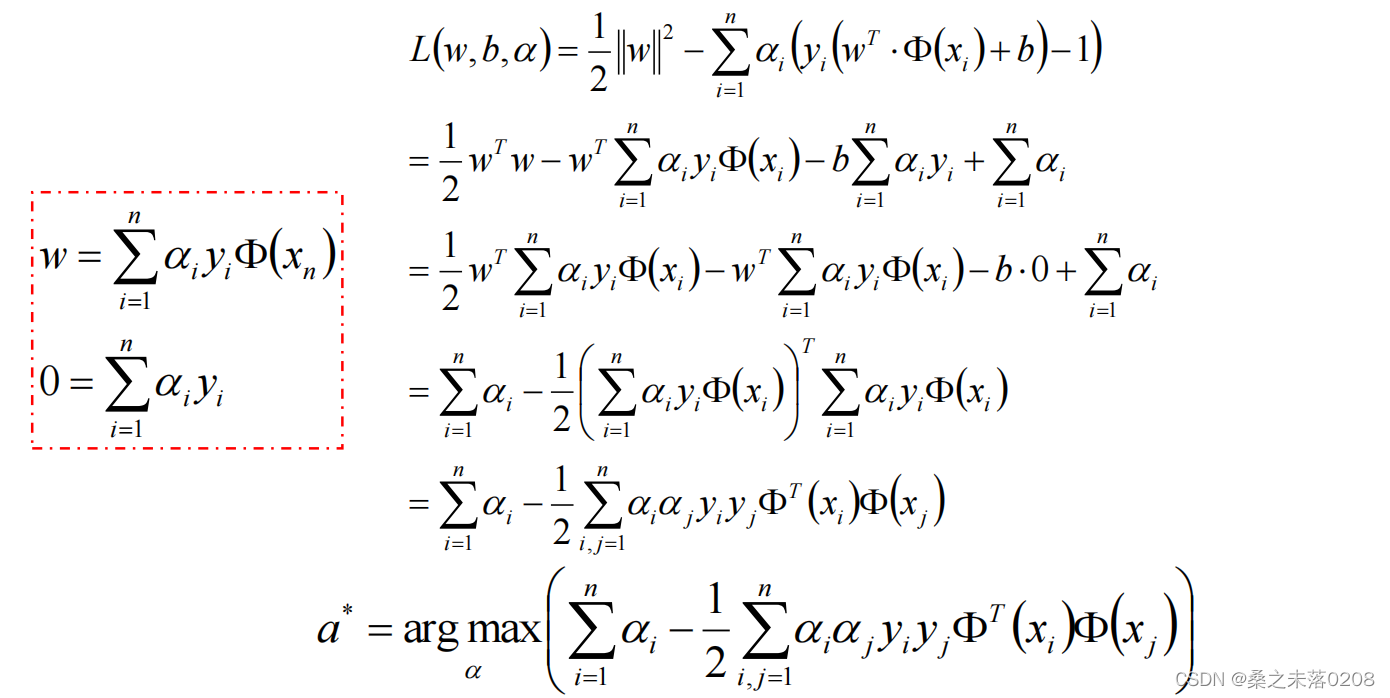
即在 Solve under constraints:
Solve under constraints:

Add a minus sign to solve:
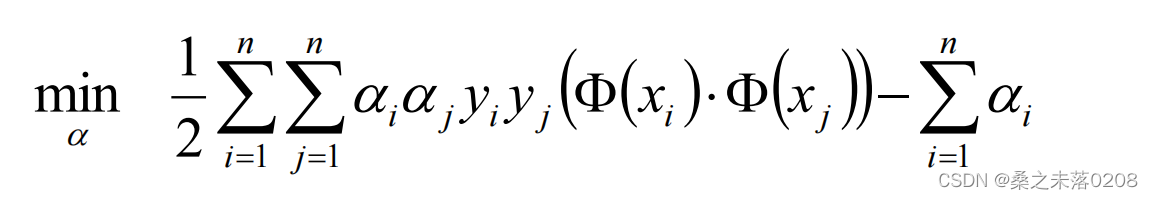

2.2 举例说明

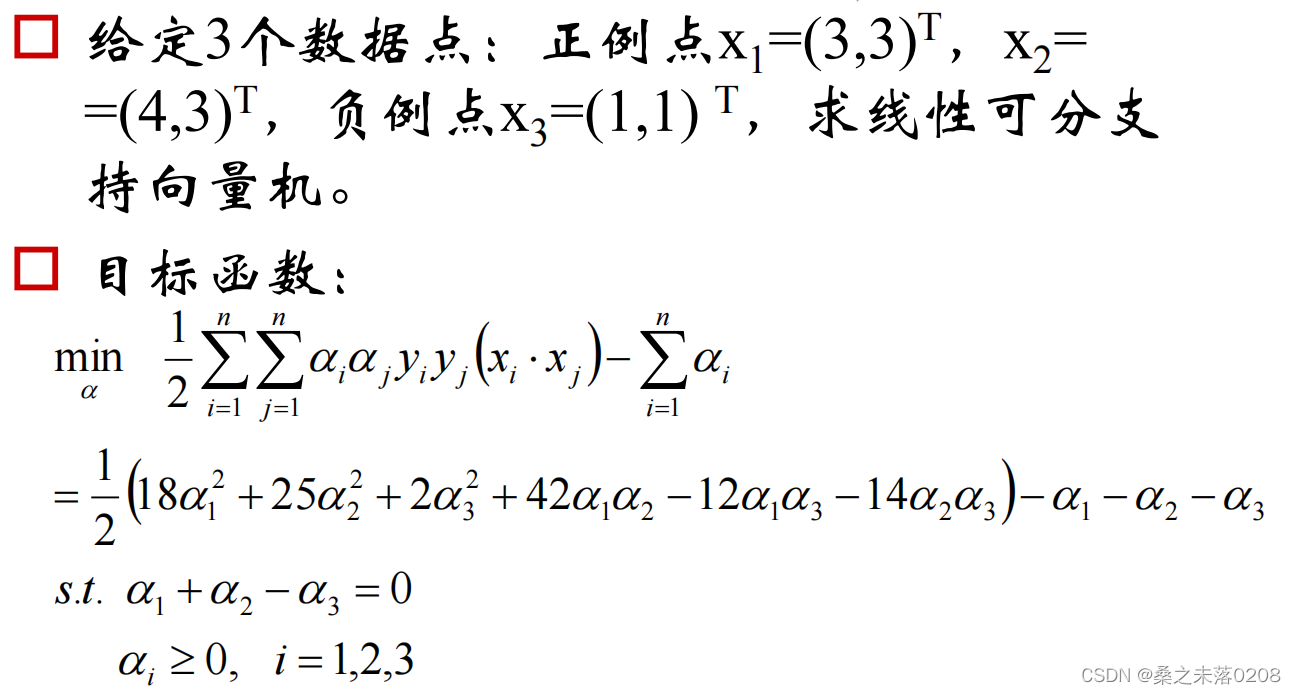

 我们可以看到
我们可以看到  ,则
,则 is a non-support vector.
is a non-support vector.
2.3 拉格朗日乘子法
约束条件: ,
,
目标:
构造函数: ,其中
,其中 任意值.
任意值.
所以
 (原始问题)
(原始问题)
对偶函数为 
所以接下来对 求导,使其为0.
求导,使其为0.
3 Understand what it means to maximize soft spacing
When the training data is approximately linearly separable,The slack variable can be increased ,通过软间隔最大化,Make the sinicization interval plus the slack variable greater than or equal to1,Thus the constraints become
,通过软间隔最大化,Make the sinicization interval plus the slack variable greater than or equal to1,Thus the constraints become ,And the objective function becomes
,And the objective function becomes 
CThe smaller the transition band, the wider,So it has generalization ability.C大时,to minimize the objective function,Actually need to make ,becomes linearly separable.
,becomes linearly separable.
所以:with relaxation factorSVM拉格朗日函数如下:




ps:Actually the loss function is 
边栏推荐
- C. Travelling Salesman and Special Numbers (二进制 + 组合数)
- MySQL String Concatenation - Various String Concatenation Practical Cases
- 宇宙的尽头是银行?聊聊在银行做软件测试的那些事
- 【MySQL系列】-B+树索引和HASH索引有什么区别
- cv2.polylines
- Database Design of Commodity Management System--SQL Server
- MYSQL unique constraint
- BGP的简单实验
- Data Lake: Data Integration Tool DataX
- LeetCode 114. Expand Binary Tree into Linked List (One Question Three Eats)
猜你喜欢
Go 学习笔记(84)— Go 项目目录结构

Reverse Analysis Practice 2

使用EFR32作为Zigbee/Thread的sniffer的用法

图像视角矫正之透视变换矩阵(单应矩阵)/findHomography 与 getPerspectiveTransformd的区别

handler+message【消息机制】

The difference between forward and redirect

宇宙的尽头是银行?聊聊在银行做软件测试的那些事

How to Effectively Conduct Retrospective Meetings (Part 1)?
![Reverse Theory Knowledge 3 [UI Modification]](/img/f3/33db96f3dd149658859be58041ab43.png)
Reverse Theory Knowledge 3 [UI Modification]

Shell script basic editing specifications and variables
随机推荐
[MRCTF2020]Hello_ misc
New LaaS protocol Elephant Swap provides ePLATO with sustainable premium space
C. Travelling Salesman and Special Numbers (二进制 + 组合数)
handler+message【消息机制】
The implementation and basic operation of sub-database sub-table, ER table, global table, fragmentation rules, global sequence, etc. in MyCat
【C进阶】数组传参与函数指针
山西省第二届网络安全技能大赛(企业组)部分赛题WP(十)
Shell script basic editing specifications and variables
DAY17、CSRF 漏洞
【Redis高手修炼之路】Jedis——Jedis的基本使用
恐造成下一个“千年虫”的闰秒,遭科技巨头们联合抵制
Notes on "The Law of Construction"---Chapter 10 Typical Users and Scenarios
MYSQL unique constraint
cnpm安装步骤
机器学习:知道通过低方差过滤实现降维过程
How to compare struct, slice, map for equality and the difference between several comparison methods in golang
[Driver] udev aliases each serial port of USB to 4 serial ports
JQ源码分析(环境处理)
软件测试员必看!数据库知识mysql查询语句大全
2.6 Merge Sort