当前位置:网站首页>Understanding and application of least square method
Understanding and application of least square method
2022-07-03 00:20:00 【TranSad】
The least square method is a familiar and strange thing .
In the regression problem, we often use the least square method to predict a straight line or curve to fit the real data points . The way to fit the data is to use the least square method —— Minimize the sum of squares of the difference between our predicted value and the real value .
Because it looks very basic and simple , Even with the above paragraph .
However , Why is the sum of squares ? Not to the power of one or three ? Because the first power will have positive and negative , Cannot express the actual distance ? Then take the absolute value with you …… I didn't think about this problem carefully , It seems that the least square method is the most commonly used and classic way anyway , It's similar to finding an Euclidean distance. It's just a kind of expression that everyone likes to use .
But actually , We can explore the origin of the least square method from the perspective of probability and statistics , So as to prove its rationality .
Origin of least square method :
Suppose we now have many sample points (x1,y1),(x2,y2),(x3,y3)……(xi,yi), We hope to predict a straight line :
y=wx+b To fit these sample points .
Step by step , First of all, this b Is intercept , It will look troublesome behind you , The common way in machine learning is actually x Add a constant term to 1, And then put b“ add to ” To w in , In this way, the straight line can be written as :

there θ More than the original w One more. b,x It is also better than the original x One more. 1, If you multiply it, there will be one more 1*b It's the original intercept .
So for each sample point , Our predictions y(i) by :
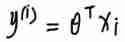
It is known that xi The corresponding actual value is yi, Suppose the error yi-y(i) by εi, Next, let's start with this error term εi Expand the analysis :
Now we have :
![]()
First of all, make it clear : Each data point has an error term εi, And these error terms obey the standard normal distribution ( The mean for 0 Standard deviation σ). So bring in the normal distribution formula , We have :

From the perspective of conditional probability , We hope that xi and θ In the case of combination yi Most likely to happen —— Is it very familiar , This is where we start using likelihood functions .( The likelihood function was originally sorted out )
We take every sample point into account ( Let them get tired ), The likelihood function is :

Now we hope to find a suitable θ Value maximizes this formula , The solution is very simple , Use the commonly used logarithmic method , You can get :

Make this formula the largest , Remove a constant term , Equivalent to minimizing the following formula :

In this way, we get the familiar least square method .
Application of least square method
Or for the example of fitting a straight line in a two-dimensional plane , We have decided to use the least square method , Then the target function is :
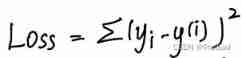
Set the format of the line as y=wx+b, Expanded :

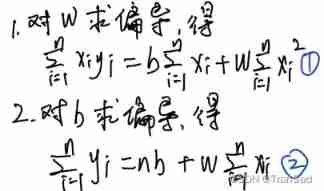
To unite , It can be solved to get the answer :

thus , We can almost get the conclusive answer of fitting a straight line in a two-dimensional plane .
Now let's take a simple concrete example :
In a two-dimensional plane , There are three points , The values are as follows :(1,1),(2,2),(3,4), Now it is required to predict a straight line to fit these data points .
( Why three points ? Because a point has no meaning , Two points determine a straight line , At three o'clock , We need to use the least square method to fit , So choose at least three points .)
Directly use the calculated conclusion , You know :
w = [3*(1*1+2*2+3*4)-(1+2+3)(1+2+4)]/[3*(1*1+2*2+3*3)-(1+2+3)*(1+2+3)] = 3/2
b = (1+2+4)/3-3/2*(1+2+3)/3 = -2/3
So a straight line can be fitted :y=3/2x-2/3, take x=1,2,3 Carry in checking calculation , It can be found that the fitting effect is really good .
The above is just a relatively simple application scenario , We can directly use a seemingly uncomplicated conclusion . Allied , We can also use the least square method to fit the conic ( At this time, we will not set f(x)=wx+b, It is y=w*x The square of +b*x The first power of +c, And then, respectively w,b,c Find the partial derivative and then solve the equation )—— in other words , We can choose different f(x) type , Different fitting curves are obtained by the least square method .( Of course , But when the situation is complicated , It is difficult for us to get a practical answer by solving the equation , At this time, we use gradient descent to directly optimize and approximate the results .)
To sum up , This article mainly combs the origin, calculation and application of the least square method , It is also used to make it convenient to review the past and know the new ~
边栏推荐
- 国外的论文在那找?
- Hit the industry directly! The propeller launched the industry's first model selection tool
- Practical series - free commercial video material library
- MFC file operation
- Angled detection frame | calibrated depth feature for target detection (with implementation source code)
- Luogu_ P1149 [noip2008 improvement group] matchstick equation_ Enumeration and tabulation
- Custom throttling function six steps to deal with complex requirements
- How QT exports data to PDF files (qpdfwriter User Guide)
- leetcode 650. 2 Keys Keyboard 只有两个键的键盘(中等)
- MFC 获取当前时间
猜你喜欢
Talk with the interviewer about the pit of MySQL sorting (including: duplicate data problem in order by limit page)

Custom throttling function six steps to deal with complex requirements
论文的英文文献在哪找(除了知网)?
Install docker and use docker to install MySQL
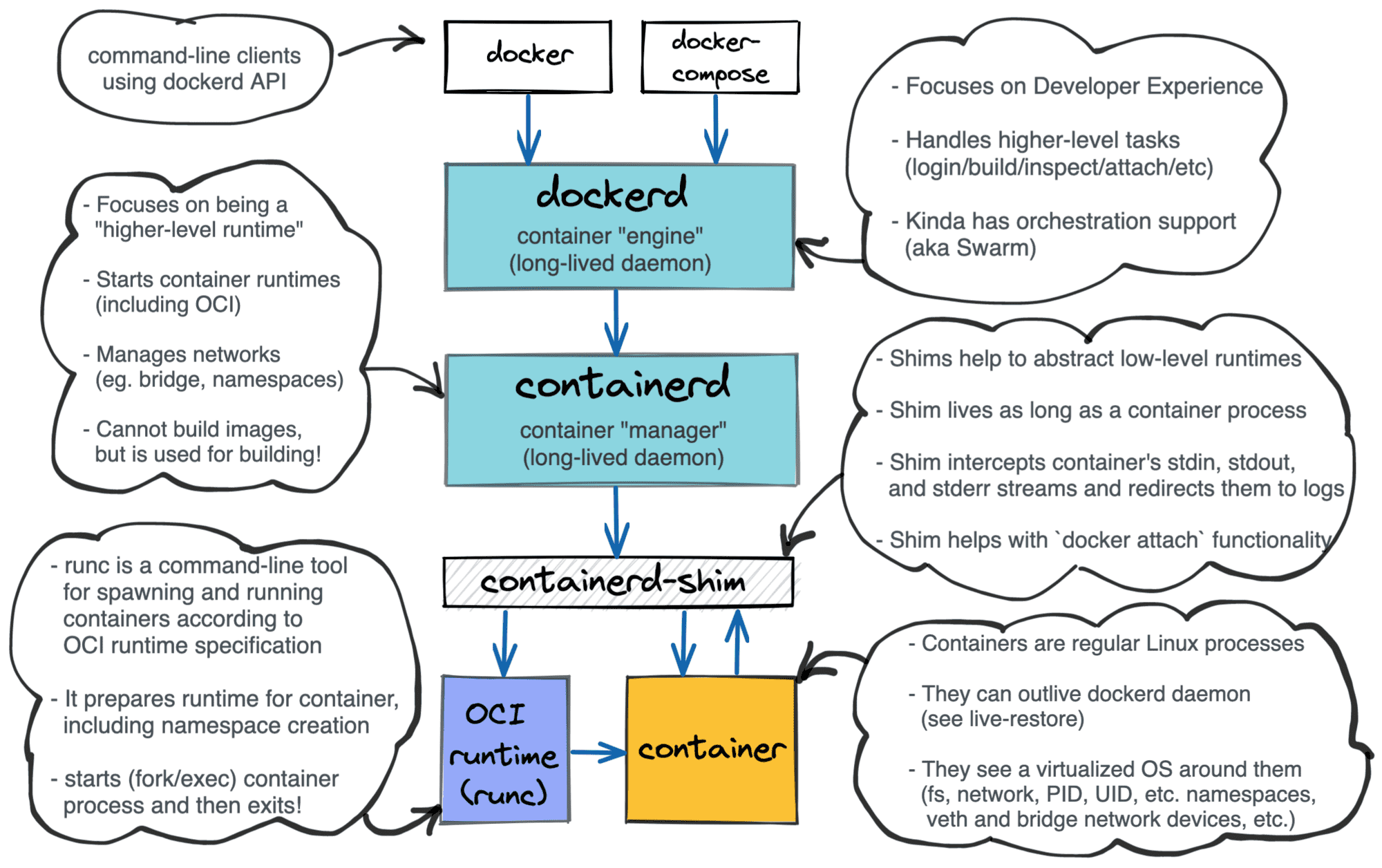
Container runtime analysis
JSON data transfer parameters

Program analysis and Optimization - 9 appendix XLA buffer assignment

How QT exports data to PDF files (qpdfwriter User Guide)

来自数砖大佬的 130页 PPT 深入介绍 Apache Spark 3.2 & 3.3 新功能

Create an interactive experience of popular games, and learn about the real-time voice of paileyun unity
随机推荐
Container runtime analysis
Linux 下安装 redis
Master the development of facial expression recognition based on deep learning (based on paddlepaddle)
来自数砖大佬的 130页 PPT 深入介绍 Apache Spark 3.2 & 3.3 新功能
Top Devops tool chain inventory
请问大家在什么网站上能查到英文文献?
哪些软件可以整篇翻译英文论文?
PR FAQ, what about PR preview video card?
[array] binary search
Open source | Wenxin big model Ernie tiny lightweight technology, which is accurate and fast, and the effect is fully open
顶级 DevOps 工具链大盘点
Bigder:32/100 测试发现的bug开发认为不是bug怎么处理
[shutter] open the third-party shutter project
CMake基本使用
MFC file operation
yolov5train. py
Architecture: load balancing
[reading notes] phased summary of writing reading notes
RTP 接发ps流工具改进(二)
【OJ】两个数组的交集(set、哈希映射 ...)