当前位置:网站首页>leetcode:210. 课程表 II
leetcode:210. 课程表 II
2022-06-12 20:47:00 【OceanStar的学习笔记】
题目来源
题目描述

题目解析
只有有向无环图才有拓扑序
拓扑排序并不是一个纯粹的排序算法,它只是针对某一类图,找到一个可以执行的线性顺序。
针对哪类图呢?有向无环图。即使:
- 这个图的边必须是有方向的;
- 图内无环。
那么什么是方向呢?
比如微信好友就是有向的,你加了他好友他可能把你删了你却不知道。。。那这个朋友关系就是单向的。。
什么是环?环是和方向有关的,从一个点出发能回到自己,这是环。
所以下图左边不是环,右边是。
那么如果一个图里有环,比如右图,想执行1就要先执行3,想执行3就要先执行2,想执行2就要先执行1,这成了个死循环,无法找到正确的打开方式,所以找不到它的一个拓扑序。
结论:
- 如果这个图不是 DAG,那么它是没有拓扑序的;
- 如果是 DAG,那么它至少有一个拓扑序;
- 反之,如果它存在一个拓扑序,那么这个图必定是 DGA。
对于本题,拓扑排序的意思是:求解一种可行的顺序,能够让我把所有课都学了。
那应该怎么做呢?
(1)首先我们可以用图来描述它,图的两个要素是顶点和边,那么在这里:
- 顶点:每门课
- 边:起点的课程是终点的课程的先修课
假如有一个这样的图:

这种图叫AOV(Activity On Vertex) 网络,在这种图里:
- 顶点:表示活动;
- 边:表示活动间的先后关系
所以一个 AOV 网应该是一个 DAG,即有向无环图,否则某些活动会无法进行。
那么所有活动可以排成一个可行线性序列,这个序列就是拓扑序列。
那么这个序列的实际意义是:
按照这个顺序,在每个项目开始时,能够保证它的前驱活动都已完成,从而使整个工程顺利进行。
回到我们这个例子中:
- 我们一眼可以看出来要先学 C1, C2,因为这两门课没有任何要求嘛,大一的时候就学呗;
- 大二就可以学第二行的 C3, C5, C8 了,因为这三门课的先修课程就是 C1, C2,我们都学完了;
- 大三可以学第三行的 C4, C9;
- 最后一年选剩下的 C6, C7。
这样,我们就把所有课程学完了,也就得到了这个图的一个拓扑排序。
注意,有时候拓扑序并不是唯一的,比如在这个例子中,先学 C1 再学 C2,和先 C2 后 C1 都行,都是这个图的正确的拓扑序,但这是两个顺序了。
所以面试的时候要问下面试官,是要求解任意解,还是列出所有解。
在这个图里的边表示的是一种依赖关系,如果要修下一门课,就要先把前一门课修了
这和打游戏里一样一样的嘛,要拿到一个道具,就要先做 A 任务,再完成 B 任务,最终终于能到达目的地了。
在上面的图里,大家很容易就看出来了它的拓扑序,但当工程越来越庞大时,依赖关系也会变得错综复杂,那就需要用一种系统性的方式方法来求解了。
那么我们回想一下刚刚自己找拓扑序的过程,为什么我们先看上了 C1, C2?
因为它们没有依赖别人啊,也就是它的入度为 0.
- 入度:顶点的入度是指「指向该顶点的边」的数量;
- 出度:顶点的出度是指该顶点指向其他点的边的数量。
所以我们先执行入度为 0 的那些点,因此我们要先记录每个顶点的入度。因为只有当它的入度为 0的时候,我们才能执行它。
在刚才的例子里,最开始 C1, C2 的入度就是 0,所以我们可以先执行这两个。
那在这个算法里第一步就是得到每个顶点的入度。
(1)预处理得到每个点的入度
我们可以用一个 HashMap 来存放这个信息,或者用一个数组会更精巧。

拿到了这个之后,就可以执行入度为 0 的这些点了,也就是 C1, C2.
那我们把可以被执行的这些点,放入一个待执行的容器里,这样之后我们一个个的从这个容器里取顶点就好了。
至于这个容器究竟选哪种数据结构,这取决于我们需要做哪些操作,再看哪种数据结构可以为之服务。
那么首先可以把**[C1, C2]**放入容器中,
然后想想我们需要哪些操作吧!
我们最常做的操作无非就是把点放进来,把点拿出去执行了,所以可以用一个queue
其他的也行,放进来这个容器里的顶点的地位都是一样的,都是可以执行的,和进来的顺序无关,但何必非得给自己找麻烦呢?一个常规顺序的简简单单的 queue 就够用了。
然后就需要把某些点拿出去执行了。
当我们把 C1 拿出来执行,那这意味这什么?
答:意味着「以 C1 为顶点」的「指向其他点」的「边」都消失了,也就是 C1 的出度变成了 0.
如下图,也就是这两条边可以消失了。
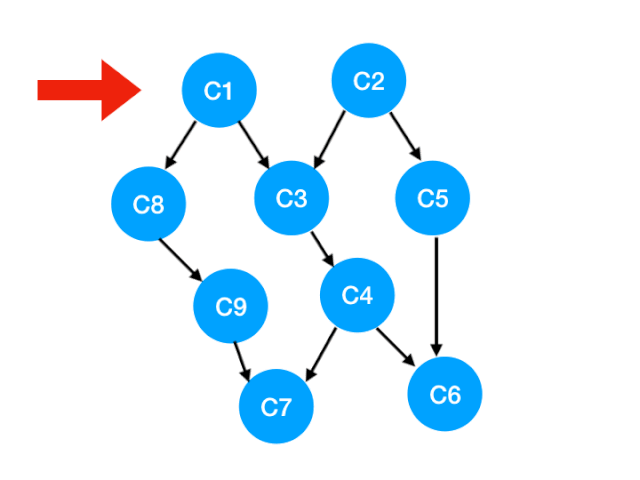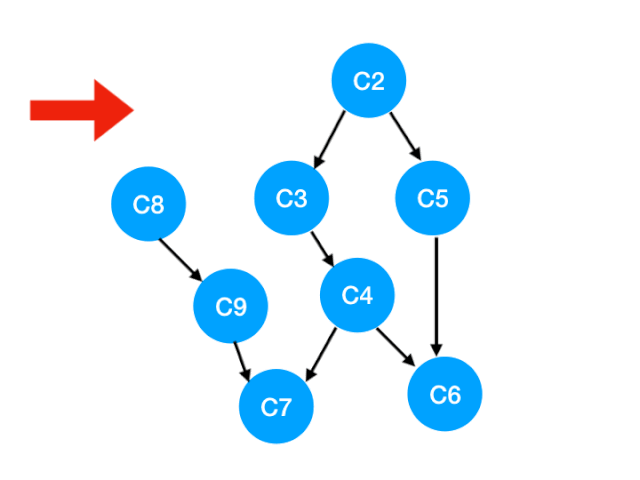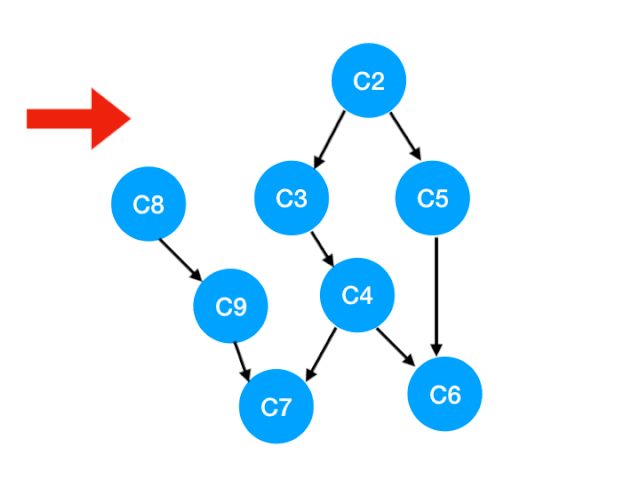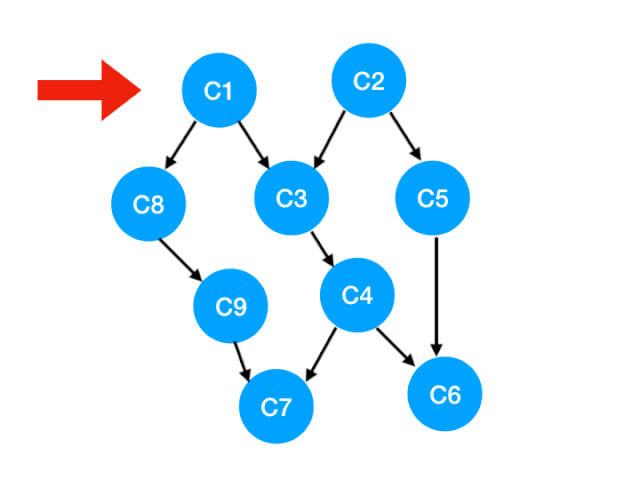
那么此时我们就可以更新 C1 所指向的那些点也就是 C3 和 C8 的 入度 了,更新后的数组如下:

那我们这里看到很关键的一步,C8 的入度变成了 0!
也就意味着 C8 此时没有了任何依赖,可以放到我们的 queue 里等待执行了。
此时我们的 queue 里就是:[C2, C8].
下一个我们再执行 C2
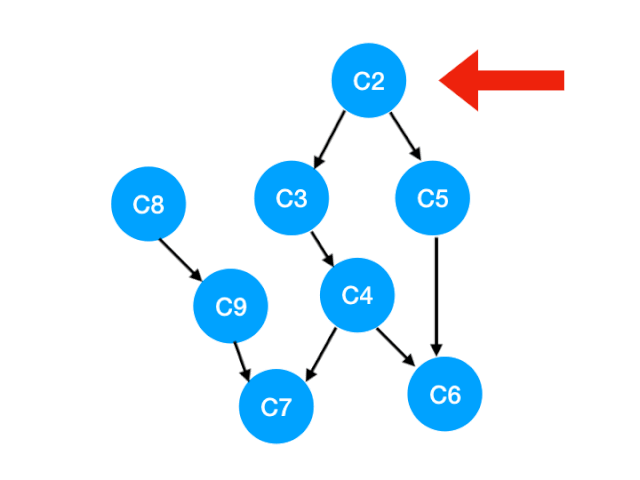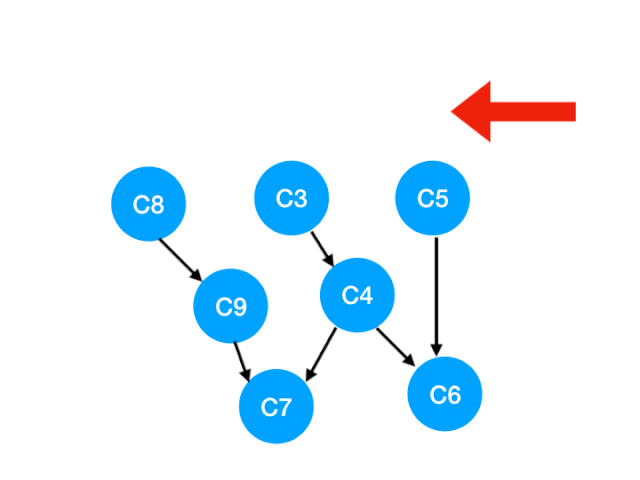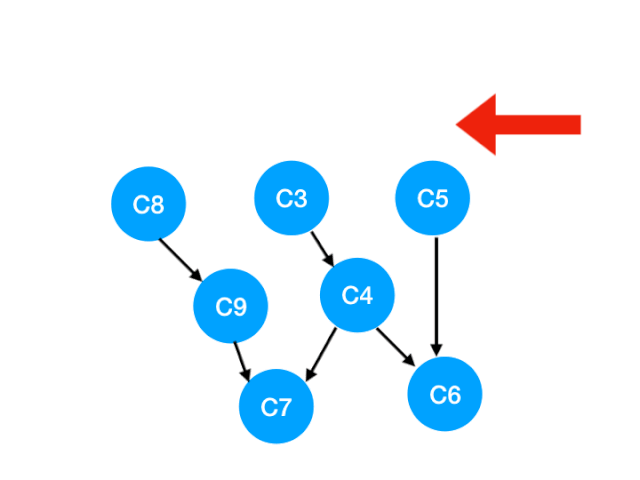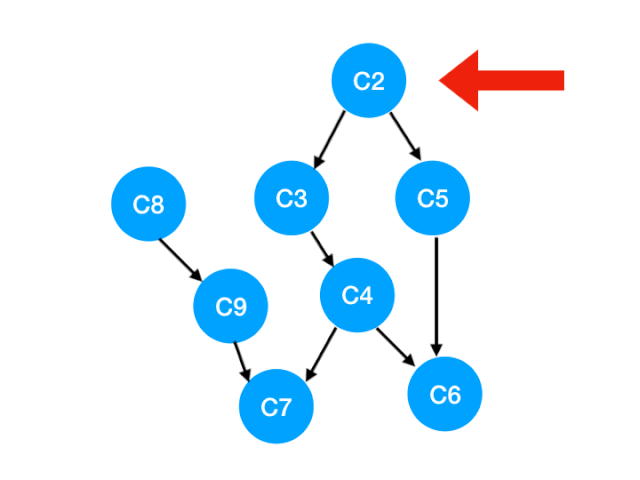
那么 C2 所指向的 C3, C5 的 入度-1,
更新表格:
也就是 C3 和 C5 都没有了任何束缚,可以放进 queue 里执行了。
queue 此时变成:[C8, C3, C5]
那么下一步我们执行 C8
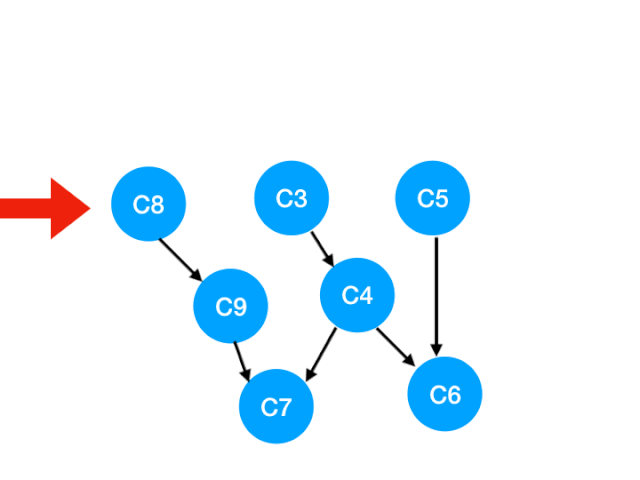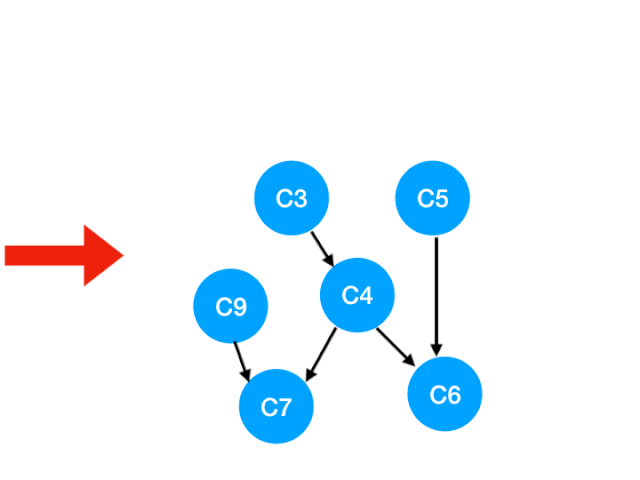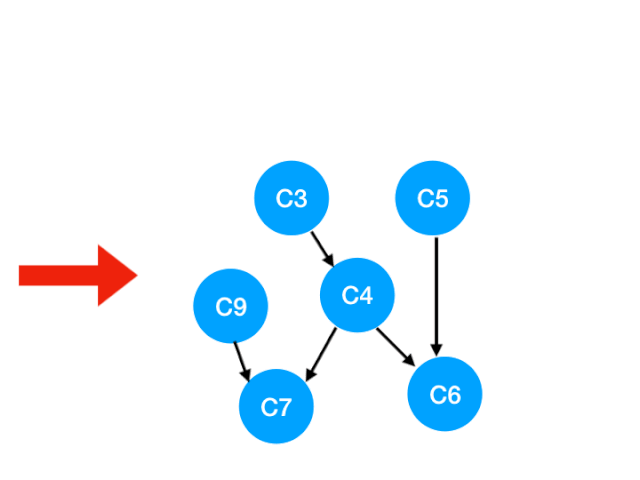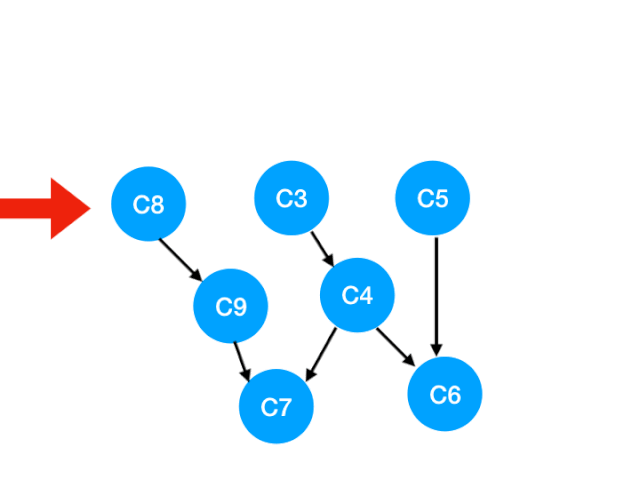
相应的 C8 所指的 C9 的入度-1.更新表格:
那么 C9 没有了任何要求,可以放进 queue 里执行了。
queue 此时变成:[C3, C5, C9]
接下来执行 C3,
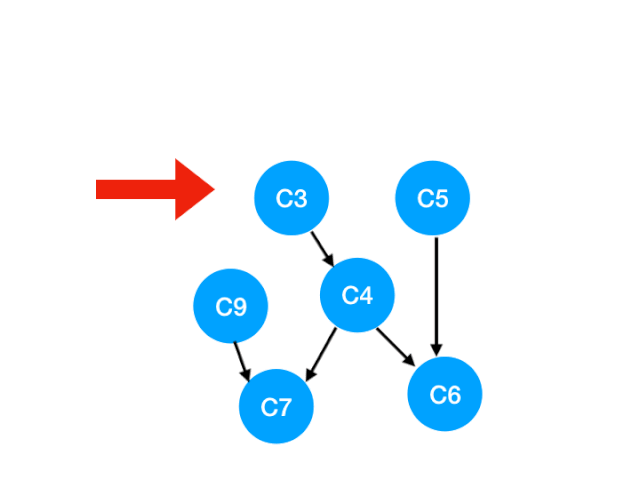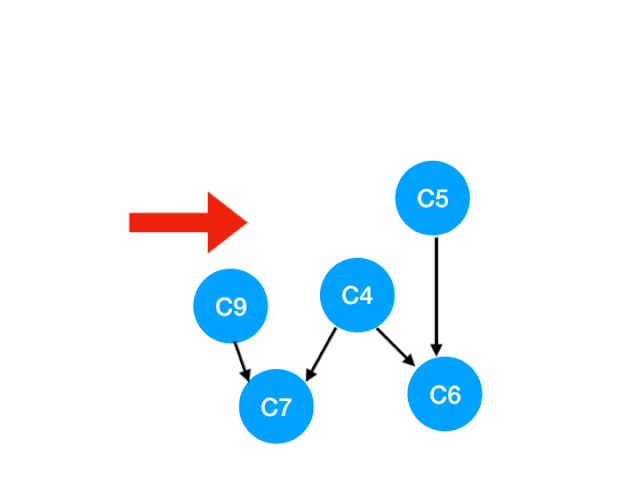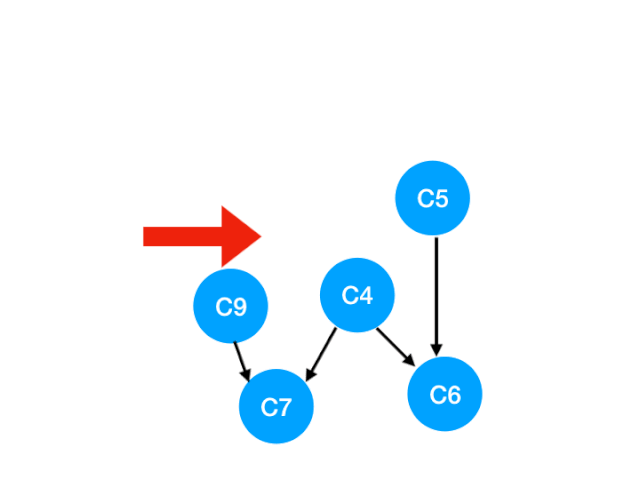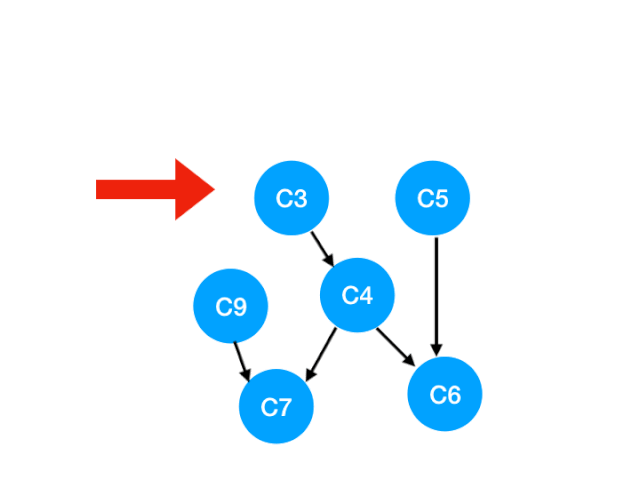
相应的 C3 所指的 C4 的入度-1.更新表格:

但是 C4 的入度并没有变成 0,所以这一步没有任何点可以加入 queue。
queue 此时变成 [C5, C9]
再执行 C5
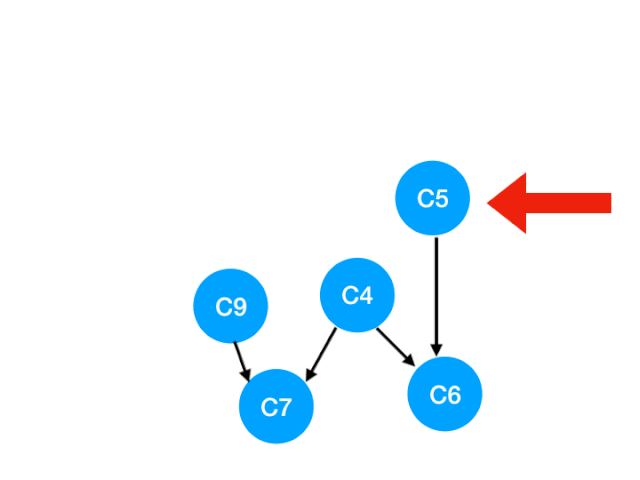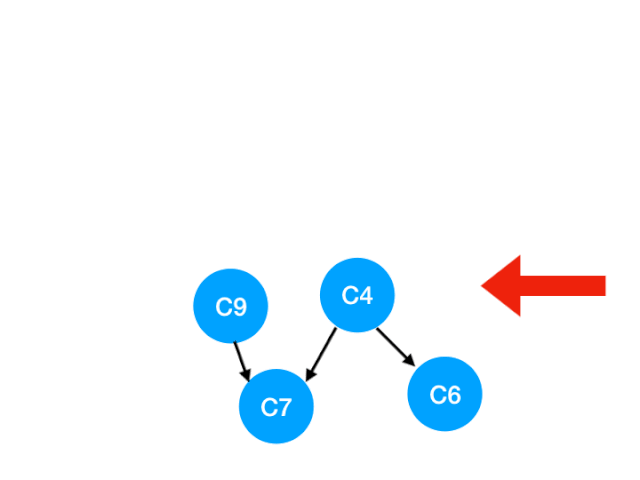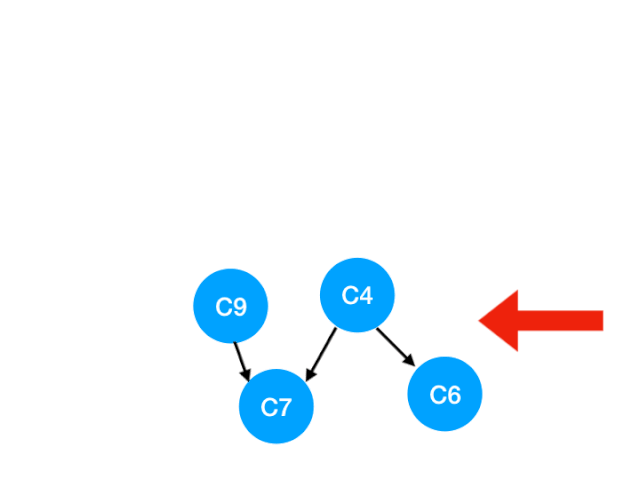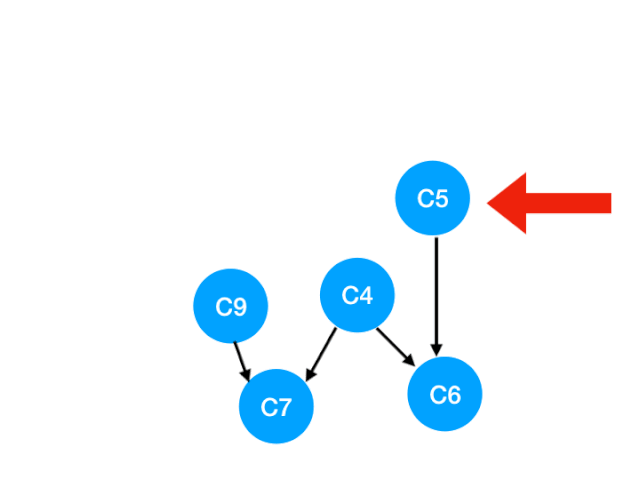
那么 C5 所指的 C4 和 C6 的入度- 1.更新表格:

这里 C4 的依赖全都消失啦,那么可以把 C4 放进 queue 里了:
queue = [C9, C4]
Step6
然后执行 C9
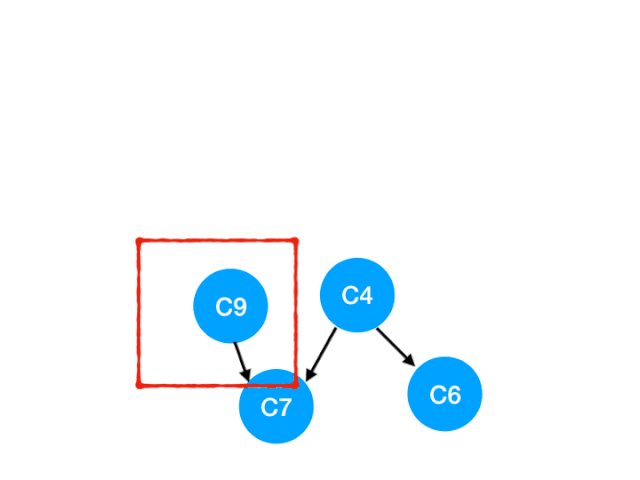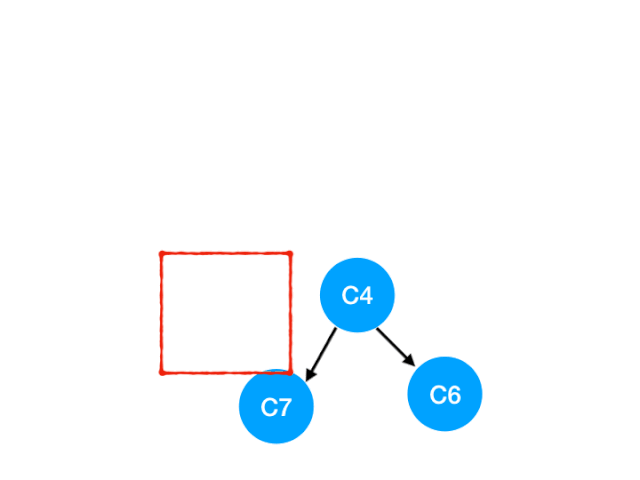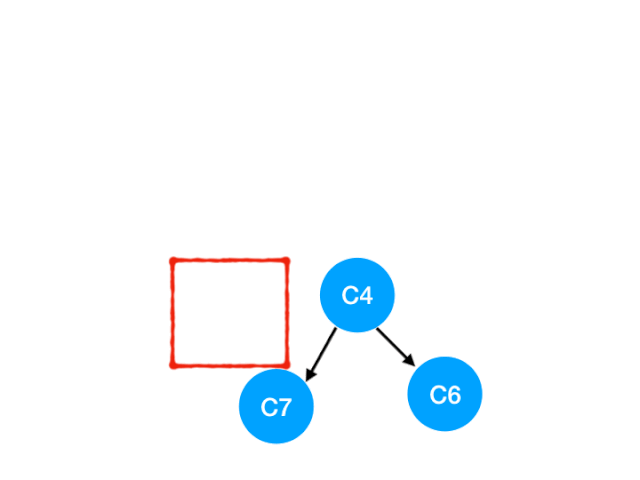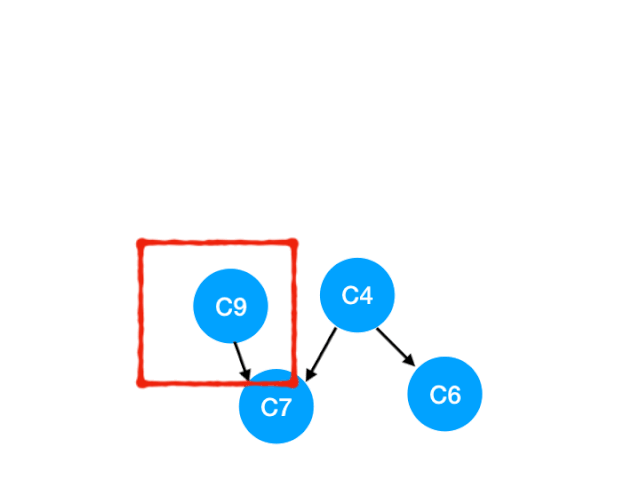
那么 C9 所指的 C7 的入度- 1

这里 C7 的入度并不为 0,还不能加入 queue,
此时 queue = [C4]
接着执行 C4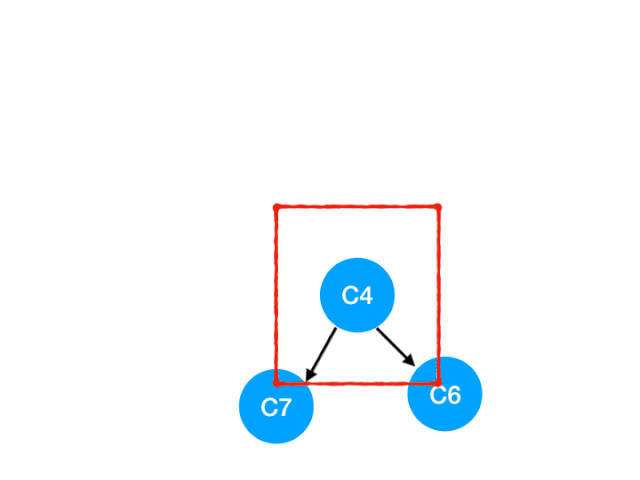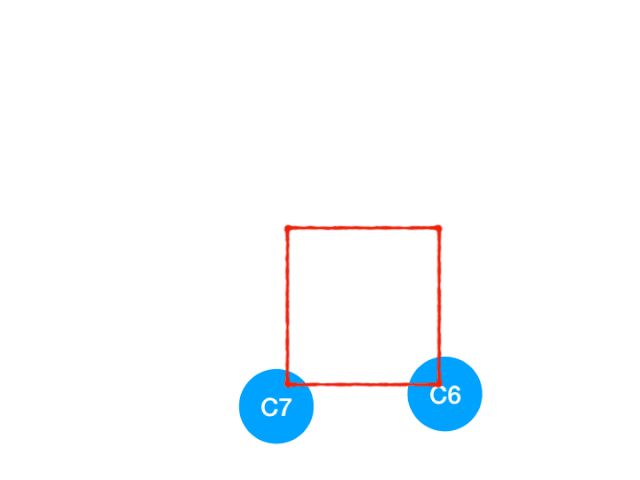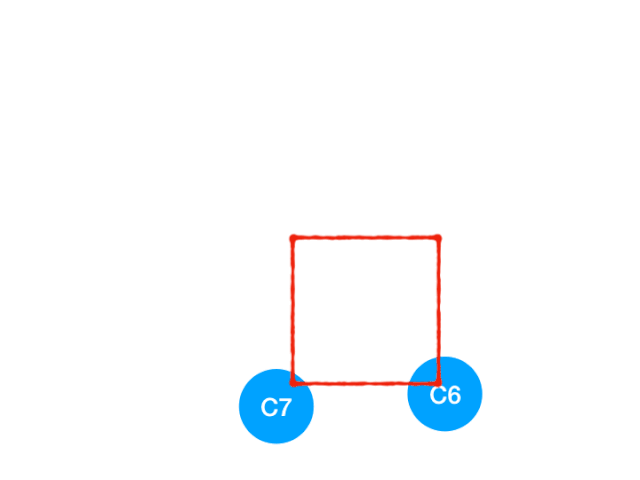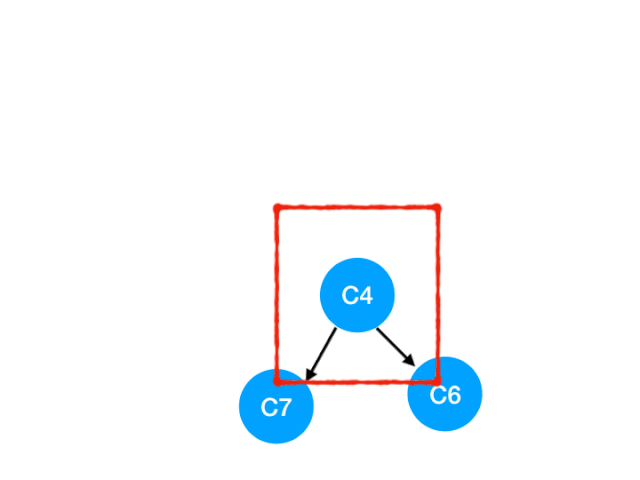
所以 C4 所指向的 C6 和 C7 的入度-1,更新表格:
C6 和 C7 的入度都变成 0 啦!!把它们放入 queue,继续执行到直到 queue 为空即可
时间复杂度
空间复杂度

边栏推荐
- China hydraulic press market trend report, technical innovation and market forecast
- How to determine fragment restored from Backstack
- Preliminary understanding of regular expressions (regex)
- 使用Swagger生成 API 文档(go语言示例)
- 同时做测试,别人已经年薪20w起,为什么你还在为达到月薪10k而努力?
- Centos7 installing MySQL 5.7
- At the same time, do the test. Others have been paid 20W a year. Why are you still working hard to reach 10K a month?
- Niuke net: somme des trois nombres
- Compréhension préliminaire des expressions régulières cognitives (regex)
- 机器学习资料汇总
猜你喜欢

设计规则检查约束(set_max_transition、set_max_capacitance)

牛客網:三數之和

In the spring recruitment of 2022, the test engineer will have a full set of interview strategies to thoroughly understand all the technical stacks (all dry goods)

中小型机房动力环境综合监控解决方案

2022年春招,测试工程师全套面试攻略,一篇吃透全部技术栈(全是干货)

Solve the cvxpy error the solver GLPK_ MI is not installed

Generate API documents using swagger (go language example)

It has been engaged in the functional test of 10K to the test development of 40W annual salary for 5 years, and spent 7 days sorting out the super comprehensive learning route
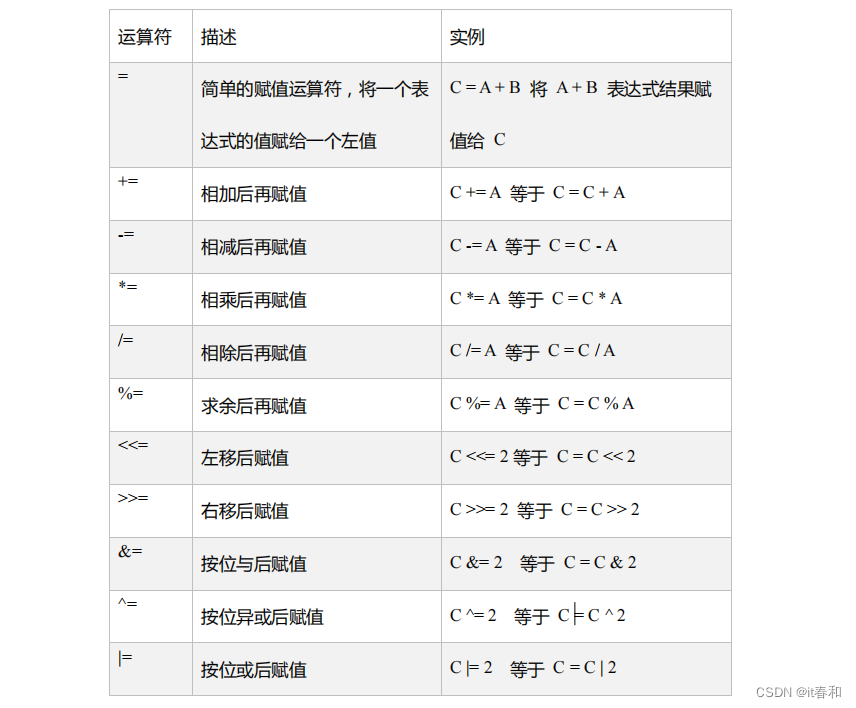
Scala基础语法入门(三)Scala中的各种运算符

Scope and scope chain
随机推荐
P5076 [Fondation profonde 16. Exemple 7] Arbre binaire commun (version simplifiée)
Solve the cvxpy error the solver GLPK_ MI is not installed
中小型机房动力环境综合监控解决方案
新品发布丨竣达智能综合环境监测终端
QT pro file configuration ffmpeg macro
How can CTCM in the inspection lot system status of SAP QM be eliminated?
P5076 【深基16.例7】普通二叉树(简化版)
DFT learning notes
EDI 855 purchase order confirmation
居家办公期间如何提升沟通效率|社区征文
Introduction to scala basic grammar (III) various operators in Scala
SAP QM preliminary - cannot assign a sampling policy to an inspection characteristic when maintaining an inspection plan by executing transaction code qp02?
测试人如何规划自己的未来?才能实现入行2年达到25k?
MySQL field truncation principle and source code analysis
Fcpx tutorial, how to export video graphics and text in Final Cut Pro?
How can the openwrt package manager image be switched to an alicloud source?
Simplest ALV template
逐向双碳:东数西算中的绿色需求与竞争焦点
Large and small end conversion
Go memory escape analysis