【torch】张量乘法:matmul,einsum

参考博文:《张量相乘matmul函数》

一、torch.matmul

matmul(input, other, out = None) 函数对 input 和 other 两个张量进行矩阵相乘。torch.matmul 函数根据传入参数的张量维度有很多重载函数。

在张量相乘的时候,并不是标准的$(m,n)\times (n,l)=(m,l)$的形式.

三、一维和二维相乘

3.1 一维乘以二维: $(m)\times (m,n)=(n)$

A1 =torch.FloatTensor(size=(4,))
A2=torch.FloatTensor(size=(4,3))
A12=torch.matmul(A1,A2)
A12.shape # (3,)

3.2 二维乘以一维: $(m,n)\ast (n)=(m)$

A3=torch.FloatTensor(size=(3,4))
A31=torch.matmul(A3,A1)
A31.shape #(3,)

四、二维和三维相乘

4.1 二维乘以3维:$(m,n)\times (b,n,l)=(b,m,l)$.扩充方案为$(b,m,n)\times (b,n,l)=(b,m,l)$

B1=torch.FloatTensor(size=(2,3))
B2=torch.FloatTensor(size=(5,3,4))
B12=torch.matmul(B1,B2)
B12.shape #(5,2,4)

等价方案:

B12_=torch.einsum("ij,bjk->bik",B1,B2)
torch.sum(B12==B12_)#40=2*4*5

4.2 三维乘以二维: $(b,m,n)\times (n,l)=(b,m,l)$.

B2=torch.FloatTensor(size=(5,3,4))
B3=torch.FloatTensor(size=(4,2))
B23=torch.matmul(B2,B3)
B23.shape #(5,3,2)

等价方案:

BB23_ =torch.einsum("bij,jk->bik",[B2,B3]) 
BB23_.shape #(5,3,2)
torch.sum(B23==BB23_)#30=5*3*2

4. 3 二维扩张为三维的方式

方式一:第一个张量二维扩张为三维

B1(2,3)–>B1_(5,2,3)

B1=torch.FloatTensor(size=(2,3))
B1_ =torch.unsqueeze(B1,axis=0)  #升维
print(B1_.shape) #torch.Size([1, 2, 3])
B11 =torch.cat([B1_,B1_,B1_,B1_,B1_],axis=0)#合并-->扩维
print(B11.shape) #torch.Size([5, 2, 3])

比较$B1(2,3)\times B2(5,3,4)与B11(5,2,3)\times B2(5,3,4)$的结果

B112=torch.matmul(B11,B2)#(5,2,3)*(5,3,4)
torch.sum(B112==B12)#40=5*2*3

说明两个值完全相同.再进一步探讨其乘法的机制.
我们拿B1(2,3)与B2(5,3,4)中的第一个矩阵相乘,看是否等于中的第一个矩阵. 如下证明是相等的

B12_0=torch.matmul(B1,B2[0])
B112[0]==B12_[0]

out:

tensor([[True, True, True, True],
        [True, True, True, True]])

2维乘以3维的矩阵演示图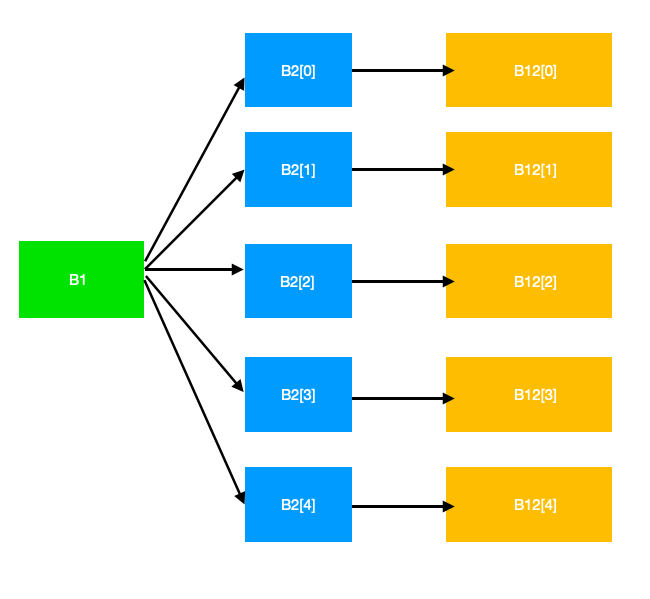

方式二:第二个张量二维扩张为三维

B3(4,2)–>B3_(5, 4, 2)

B3_=torch.unsqueeze(B3,axis=0)
print(B3_.shape)#(1,4,2)
B33 =torch.cat([B3_,B3_,B3_,B3_,B3_],axis=0)
print(B33.shape)#(5,4,2)
B233 =torch.matmul(B2,B33)
print(B233.shape) #(5,3,2)

比较两种乘法的结果：

print(torch.sum(B233==B23_)) #30
print(torch.sum(B233==B23)) #30

提醒：torch的FloatTensor中出现了nan值,似乎会不相等.

五、二维和四维相乘

5.1 二维乘以四维：$(m,n)\times (b,c,n,l)=(b,c,m,l)$

B1=torch.FloatTensor(size=(2,3))
B4 =torch.FloatTensor(size=(7,5,3,4))
B14 =torch.matmul(B1,B4)
print(B14.shape) #(7, 5, 2, 4)

等价方案

B14_= torch.einsum("mn,bcnl->bcml",[B1,B4])
print(torch.sum(B14==B14_))#280=7*5*2*4

升维

## 升维
B11 = torch.unsqueeze(B1,dim=0)
B11 = torch.concat([B11,B11,B11,B11,B11],dim=0)
print(B11.shape)#(5,2,3)
B111 = torch.unsqueeze(B11,dim=0)
B111 =torch.concat([B111,B111,B111,B111,B111,B111,B111],dim = 0)
print(B111.shape)#(7,5,2,3)

广播后的4维乘以4维

B1114 = torch.matmul(B111,B4)
print(B1114.shape)#(7,5,3,4)
print(torch.sum(B1114==B14))#280

5.2 四维乘以二维：$(b,c,n,l)\times (l,p)=(b,c,n,p)$

4维乘以2维

B43 = torch.matmul(B4,B3)
print("B43 shape",B43.shape) #(7,5,3,2)

等价形式

B43_ = torch.einsum("bcnl,lp->bcnp",[B4,B3])
print("B4 is nan",torch.sum(B4.isnan()))#0
print(torch.sum(B43==B43_))#210 =7*5*3*2

升维

B33 =torch.unsqueeze(B3,dim=0)
B33 = torch.concat([B33,B33,B33,B33,B33],dim =0)
B333 = torch.unsqueeze(B33,dim =0)
B333 =torch.concat([B333,B333,B333,B333,B333,B333,B333],dim =0)
print("B333 shape is",B333.shape)#(7,5,4,2)

广播后4维乘以4维

B4333 =torch.matmul(B4,B333)
print("B4333 shape is",B4333.shape)#(7,5,3,2)