当前位置:网站首页>P6698-[balticoi 2020 day2] virus [AC automata, DP, SPFA]
P6698-[balticoi 2020 day2] virus [AC automata, DP, SPFA]
2022-06-24 09:22:00 【QuantAsk】
On the subject
Topic link :https://www.luogu.com.cn/problem/P6698
The main idea of the topic
There is a 0 ∼ G − 1 0\sim G-1 0∼G−1 Character set for , Among them is n n n Two transformations , Be able to put a character a i ( a i > 1 ) a_i(a_i>1) ai(ai>1) Become a string of characters b i b_i bi, When only... Is left in a string 0 0 0 and 1 1 1 The hour shift is over .
Then give m m m Matching strings c i c_i ci. Now for each character i ∈ [ 2 , G − 1 ] i\in[2,G-1] i∈[2,G−1], Character or not i i i It contains at least one matching string at the end of the change , If not , Find the shortest final string length that does not contain any matching strings .
Make sure that everyone is in [ 2 , G − 1 ] [2,G-1] [2,G−1] All characters can be changed , The matching string contains only 0 / 1 0/1 0/1.
∑ t i ≤ 50 , ∑ ∣ b i ∣ ≤ 100 , n ≤ 100 , 2 < G ≤ n + 2 \sum t_i\leq 50,\sum |b_i|\leq 100,n\leq 100,2<G\leq n+2 ∑ti≤50,∑∣bi∣≤100,n≤100,2<G≤n+2
Their thinking
There are matching problems , Let's take all of them first c i c_i ci Come out and build one AC automata , Then consider how to calculate which state each character can jump from .
Notice that we are AC An automaton cannot go to a state containing a matching string when it goes to a state , In this way, we can regard including matching string as the shortest length without matching string is infinite .
So let's consider dp The shortest length , set up f i , s , t f_{i,s,t} fi,s,t According to the character i i i After transformation , From the State s s s Go to status t t t The shortest length of .
When transferring, we consider enumerating a transformation i i i, Enumerate another starting point s s s, Then set g j , x g_{j,x} gj,x It means to go to now b i , j b_{i,j} bi,j, In state x x x The shortest length of time , Then there is
g j + 1 , y = m i n { g j , x + f b i , j , x , y } g_{j+1,y}=min\{g_{j,x}+f_{b_{i,j},x,y}\} gj+1,y=min{ gj,x+fbi,j,x,y}
But you will notice f i , s , t f_{i,s,t} fi,s,t The transfer between is not a one-way relationship , You will find that this is a transfer very similar to the shortest path , Let's consider a magic change SPFA.
Let's put the 0 , 1 0,1 0,1 Join the queue , Then take out the team leader each time x x x, We put all containing characters x x x Of b i b_i bi Take them out and run once g g g, If you come out this time g g g Be able to update f a i , s , t f_{a_i,s,t} fai,s,t, Then we will a i a_i ai The team ( If before a i a_i ai Not in line ).
We see SPFA The complexity of is O ( n 2 ) O(n^2) O(n2), remember AC The number of automata States is k k k, Each transfer should be O ( ∣ b i ∣ k 3 ) O(|b_i|k^3) O(∣bi∣k3), So in this question SPFA The complexity of should be O ( G ∑ ∣ b i ∣ k 3 ) O(G\sum |b_i|k^3) O(G∑∣bi∣k3), In fact, the running constant will be very small , Can pass this problem .
code
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<vector>
#define ll long long
using namespace std;
const ll N=105,inf=1e18;
ll G,n,m,a[N],f[N][N][N],g[N][52];
ll cnt,ch[N][2],fail[N];bool ed[N],v[N];
queue<int> q;vector<int> b[N],T[N];
void ins(ll n){
ll x=0;
for(ll i=1,c;i<=n;i++){
scanf("%lld",&c);
if(!ch[x][c])ch[x][c]=++cnt;
x=ch[x][c];
}
ed[x]=1;return;
}
void getfail(){
for(ll i=0;i<2;i++)
if(ch[0][i])q.push(ch[0][i]);
while(!q.empty()){
ll x=q.front();q.pop();
ed[x]|=ed[fail[x]];
for(ll i=0;i<2;i++){
if(ch[x][i]){
fail[ch[x][i]]=ch[fail[x]][i];
q.push(ch[x][i]);
}
else ch[x][i]=ch[fail[x]][i];
}
}
return;
}
bool solve(int i){
bool flag=0;
for(ll s=0;s<=cnt;s++){
if(ed[s])continue;
memset(g,0x3f,sizeof(g));g[0][s]=0;
for(ll j=0;j<b[i].size();j++){
for(ll x=0;x<=cnt;x++){
if(g[j][x]>=inf)continue;
for(ll y=0;y<=cnt;y++)
g[j+1][y]=min(g[j+1][y],g[j][x]+f[b[i][j]][x][y]);
}
}
for(ll x=0;x<=cnt;x++){
flag|=(g[b[i].size()][x]<f[a[i]][s][x]);
f[a[i]][s][x]=min(f[a[i]][s][x],g[b[i].size()][x]);
}
}
return flag;
}
void SPFA(){
q.push(0);q.push(1);v[0]=v[1]=1;
while(!q.empty()){
int x=q.front();q.pop();v[x]=0;
for(int i=0;i<T[x].size();i++){
int y=T[x][i];
if(solve(y)&&!v[a[y]])
q.push(a[y]),v[a[y]]=1;
}
}
return;
}
signed main()
{
scanf("%lld%lld%lld",&G,&n,&m);
for(ll i=1,k;i<=n;i++){
scanf("%lld%lld",&a[i],&k);
for(ll j=1,x;j<=k;j++){
scanf("%lld",&x),b[i].push_back(x);
T[x].push_back(i);
}
}
for(ll i=1,k;i<=m;i++){
scanf("%lld",&k);
ins(k);
}
getfail();ll k=0;
memset(f,0x3f,sizeof(f));
for(ll i=0;i<=cnt;i++){
if(ed[i])continue;
if(!ed[ch[i][0]])f[0][i][ch[i][0]]=1;
if(!ed[ch[i][1]])f[1][i][ch[i][1]]=1;
}
SPFA();
for(ll i=2;i<G;i++){
ll ans=inf;
for(ll x=0;x<=cnt;x++)
ans=min(ans,f[i][0][x]);
if(ans>=inf)puts("YES");
else printf("NO %lld\n",ans);
}
return 0;
}
边栏推荐
- Vidéo courte recommandée chaque semaine: Soyez sérieux en parlant de "métaunivers"
- [noi Simulation Competition] send (tree DP)
- linux(centos7.9)安装部署mysql-cluster 7.6
- How to import MDF and LDF files into MySQL workbench
- Qingcloud based R & D cloud solution for geographic information enterprises
- 【LeetCode】415. String addition
- 学习太极创客 — ESP8226 (十二)ESP8266 多任务处理
- 小白学习MySQL - 增量统计SQL的需求
- leetcode--链表
- 2022-06-23: given a nonnegative array, select any number to make the maximum cumulative sum a multiple of 7, and return the maximum cumulative sum. N is larger, to the 5th power of 10. From meituan. 3
猜你喜欢

活动报名|Apache Pulsar x KubeSphere 在线 Meetup 火热报名中

How to configure environment variables and distinguish environment packaging for multi terminal project of uniapp development
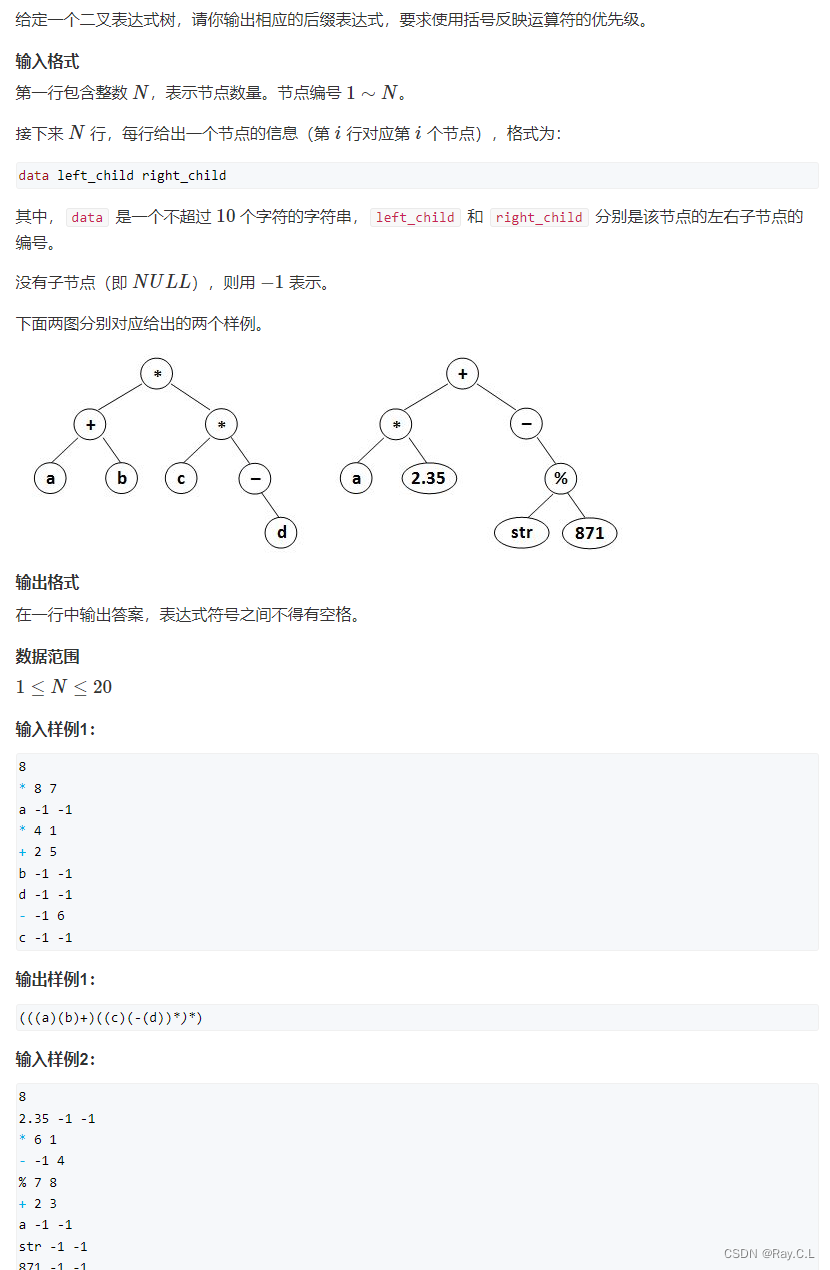
4274. suffix expression
![[Niuke] convert string to integer](/img/56/3e491b3d0eea0d89a04d0b871501d7.png)
[Niuke] convert string to integer

ApplicationContextInitializer的三种使用方法

Zero foundation self-study SQL course | related sub query

支持向量机(SVC,NuSVC,LinearSVC)

Groovy通过withCredentials获取Jenkins凭据

NETRCA: AN EFFECTIVE NETWORK FAULT CAUSE LOCALIZATION之论文阅读
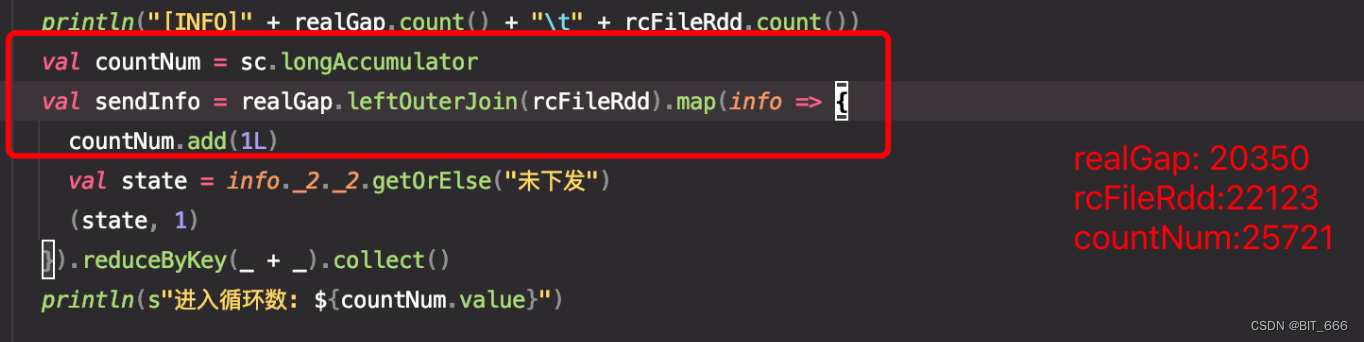
Spark - the number of leftouterjoin results is inconsistent with that of the left table
随机推荐
Zero foundation self-study SQL course | having clause
Huawei Router: IPSec Technology
[redis implements seckill business ①] seckill process overview | basic business implementation
2021-05-20computed and watch applications and differences
Weekly recommended short video: is the ultimate form of computing "meta universe"?
The native applet uses canvas to make posters, which are scaled to the same scale. It is similar to the uniapp, but the writing method is a little different
P6698-[BalticOI 2020 Day2]病毒【AC自动机,dp,SPFA】
Spark - the number of leftouterjoin results is inconsistent with that of the left table
每周推荐短视频:谈论“元宇宙”要有严肃认真的态度
threejs辉光通道01(UnrealBloomPass && layers)
Project deployment related
eBanb B1手环刷固件异常中断处理
Yolox backbone -- implementation of cspparknet
Data middle office: overview of data governance
零基础自学SQL课程 | SQL语句语法顺序与执行顺序
Data midrange: analysis of full stack technical architecture of data midrange, with industry solutions
Code written by mysql, data addition, deletion, query and modification, etc
Common emoticons
Linux MySQL installation
普通人没有学历,自学编程可以月入过万吗?