当前位置:网站首页>Advanced Mathematics (Seventh Edition) Tongji University exercises 1-2 personal solutions
Advanced Mathematics (Seventh Edition) Tongji University exercises 1-2 personal solutions
2022-06-13 03:57:00 【Navigator_ Z】
Advanced mathematics ( The seventh edition ) Tongji University exercises 1-2
1. Next Column various topic in , which some Count Column closed Convergence , which some Count Column Hair scattered ? Yes closed Convergence Count Column , through too view Observe ∣ X n ∣ Of change turn Trend potential , Write Out it People Of extremely limit : \begin{aligned}&1. Of the following questions , Which sequences converge , Which series diverge ? On convergent sequence , Through observation |X_n| Change trend of ,\\\\& Write their limits :&\end{aligned} 1. Next Column various topic in , which some Count Column closed Convergence , which some Count Column Hair scattered ? Yes closed Convergence Count Column , through too view Observe ∣Xn∣ Of change turn Trend potential , Write Out it People Of extremely limit :
( 1 ) { 1 2 n } ; ( 2 ) { ( − 1 ) n 1 n } ; ( 3 ) { 2 + 1 n 2 } ; ( 4 ) { n − 1 n + 1 } ; ( 5 ) { n ( − 1 ) n } ; ( 6 ) { 2 n − 1 3 n } ; ( 7 ) { n − 1 n } ; ( 8 ) { [ ( − 1 ) n + 1 ] n + 1 n } \begin{aligned} &\ \ (1)\ \left\{\frac{1}{2^n}\right\};\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)\ \left\{(-1)^n\frac{1}{n}\right\};\\\\ &\ \ (3)\ \left\{2+\frac{1}{n^2}\right\};\ \ \ \ \ \ \ \ \ (4)\ \left\{\frac{n-1}{n+1}\right\};\\\\ &\ \ (5)\ \{n(-1)^n\};\ \ \ \ \ \ \ \ \ \ \ \ (6)\ \left\{\frac{2^n-1}{3^n}\right\};\\\\ &\ \ (7)\ \left\{n-\frac{1}{n}\right\};\ \ \ \ \ \ \ \ \ \ \ (8)\ \left\{[(-1)^n+1]\frac{n+1}{n}\right\} & \end{aligned} (1) { 2n1}; (2) { (−1)nn1}; (3) { 2+n21}; (4) { n+1n−1}; (5) { n(−1)n}; (6) { 3n2n−1}; (7) { n−n1}; (8) { [(−1)n+1]nn+1}
Explain :
( 1 ) When n → ∞ when , 1 2 n Trend towards On 0 , because this Count Column yes closed Convergence Of , lim n → ∞ 1 2 n = 0 ( 2 ) When n → ∞ when , ( − 1 ) n 1 n Trend towards On 0 , because this Count Column yes closed Convergence Of , lim n → ∞ ( − 1 ) n 1 n = 0 ( 3 ) When n → ∞ when , 1 n 2 Trend towards On 0 , namely 2 + 1 n 2 Trend towards On 2 , because this Count Column yes closed Convergence Of , lim n → ∞ ( 2 + 1 n 2 ) = 2 ( 4 ) n − 1 n + 1 = 1 − 1 n 1 + 1 n , When n → ∞ when , 1 − 1 n 1 + 1 n Trend towards On 1 , because this Count Column yes closed Convergence Of , lim n → ∞ n − 1 n + 1 = 1 ( 5 ) When n → ∞ when , n ( − 1 ) n Trend towards On ∞ , because this Count Column yes Hair scattered Of . ( 6 ) 2 n − 1 3 n = ( 2 3 ) n − 1 3 n , When n → ∞ when , ( 2 3 ) n − 1 3 n Trend towards On 0 , because this Count Column yes closed Convergence Of , lim n → ∞ 2 n − 1 3 n = 0 ( 7 ) When n → ∞ when , n − 1 n Trend towards On ∞ , because this Count Column yes Hair scattered Of . ( 8 ) [ ( − 1 ) n + 1 ] n + 1 n = [ ( − 1 ) n + 1 ] ( 1 + 1 n ) , When n → ∞ when , [ ( − 1 ) n + 1 ] ( 1 + 1 n ) Trend towards On back complex stay Count word 0 , 2 jump dynamic , because this Count Column yes Hair scattered Of . \begin{aligned} &\ \ (1)\ When n \rightarrow \infty when ,\frac{1}{2^n} Tend to 0, So the sequence is convergent ,\lim_{n \rightarrow \infty}\frac{1}{2^n}=0\\\\ &\ \ (2)\ When n \rightarrow \infty when ,(-1)^n\frac{1}{n} Tend to 0, So the sequence is convergent ,\lim_{n \rightarrow \infty}(-1)^n\frac{1}{n}=0\\\\ &\ \ (3)\ When n \rightarrow \infty when ,\frac{1}{n^2} Tend to 0, namely 2+\frac{1}{n^2} Tend to 2, So the sequence is convergent ,\lim_{n \rightarrow \infty}\left(2+\frac{1}{n^2}\right)=2\\\\ &\ \ (4)\ \frac{n-1}{n+1}=\frac{1-\frac{1}{n}}{1+\frac{1}{n}}, When n \rightarrow \infty when ,\frac{1-\frac{1}{n}}{1+\frac{1}{n}} Tend to 1, So the sequence is convergent ,\lim_{n \rightarrow \infty}\frac{n-1}{n+1}=1\\\\ &\ \ (5)\ When n \rightarrow \infty when ,n(-1)^n Tend to \infty, So the sequence is divergent .\\\\ &\ \ (6)\ \frac{2^n-1}{3^n}=\left(\frac{2}{3}\right)^n-\frac{1}{3^n}, When n \rightarrow \infty when ,\left(\frac{2}{3}\right)^n-\frac{1}{3^n} Tend to 0, So the sequence is convergent ,\lim_{n \rightarrow \infty}\frac{2^n-1}{3^n}=0\\\\ &\ \ (7)\ When n \rightarrow \infty when ,n-\frac{1}{n} Tend to \infty, So the sequence is divergent .\\\\ &\ \ (8)\ [(-1)^n+1]\frac{n+1}{n}=[(-1)^n+1]\left(1+\frac{1}{n}\right), When n \rightarrow \infty when ,[(-1)^n+1]\left(1+\frac{1}{n}\right) Tends to repeat in numbers 0,2 beating ,\\\\&\ \ So the sequence is divergent .\\\\ & \end{aligned} (1) When n→∞ when ,2n1 Trend towards On 0, because this Count Column yes closed Convergence Of ,n→∞lim2n1=0 (2) When n→∞ when ,(−1)nn1 Trend towards On 0, because this Count Column yes closed Convergence Of ,n→∞lim(−1)nn1=0 (3) When n→∞ when ,n21 Trend towards On 0, namely 2+n21 Trend towards On 2, because this Count Column yes closed Convergence Of ,n→∞lim(2+n21)=2 (4) n+1n−1=1+n11−n1, When n→∞ when ,1+n11−n1 Trend towards On 1, because this Count Column yes closed Convergence Of ,n→∞limn+1n−1=1 (5) When n→∞ when ,n(−1)n Trend towards On ∞, because this Count Column yes Hair scattered Of . (6) 3n2n−1=(32)n−3n1, When n→∞ when ,(32)n−3n1 Trend towards On 0, because this Count Column yes closed Convergence Of ,n→∞lim3n2n−1=0 (7) When n→∞ when ,n−n1 Trend towards On ∞, because this Count Column yes Hair scattered Of . (8) [(−1)n+1]nn+1=[(−1)n+1](1+n1), When n→∞ when ,[(−1)n+1](1+n1) Trend towards On back complex stay Count word 0,2 jump dynamic , because this Count Column yes Hair scattered Of .
2. ( 1 ) Count Column Of Yes world sex yes Count Column closed Convergence Of What Well strip Pieces of ? ( 2 ) nothing world Count Column yes no One set Hair scattered ? ( 3 ) Yes world Count Column yes no One set closed Convergence ? \begin{aligned}&2. \ (1) The boundedness of a sequence of numbers is a condition for the convergence of a sequence of numbers ?\\\\&\ \ \ \ (2) Whether the unbounded sequence of numbers must diverge ?\\\\&\ \ \ \ (3) Whether a bounded sequence of numbers must converge ?&\end{aligned} 2. (1) Count Column Of Yes world sex yes Count Column closed Convergence Of What Well strip Pieces of ? (2) nothing world Count Column yes no One set Hair scattered ? (3) Yes world Count Column yes no One set closed Convergence ?
Explain :
( 1 ) Count Column Of Yes world sex yes Count Column closed Convergence Of have to want strip Pieces of . ( 2 ) nothing world Count Column One set Hair scattered . ( 3 ) Yes world Count Column No One set closed Convergence . \begin{aligned} &\ \ (1)\ The boundedness of sequence is a necessary condition for the convergence of sequence .\\\\ &\ \ (2)\ Unbounded sequences must diverge .\\\\ &\ \ (3)\ Bounded sequences do not necessarily converge .\\\\ & \end{aligned} (1) Count Column Of Yes world sex yes Count Column closed Convergence Of have to want strip Pieces of . (2) nothing world Count Column One set Hair scattered . (3) Yes world Count Column No One set closed Convergence .
3. Next Column Turn off On Count Column ∣ x n ∣ Of extremely limit yes a Of set The righteous , which some yes Yes Of , which some yes wrong Of ? Such as fruit yes Yes Of , try say bright The reason is from ; Such as fruit yes wrong Of , try to Out One individual back example . \begin{aligned}&3. \ The following is about the sequence |x_n| The limit of a The definition of , What is right , What's wrong ? If it's right , Try to explain why ; If it's wrong ,\\\\&\ \ \ \ Try to give a counterexample .&\end{aligned} 3. Next Column Turn off On Count Column ∣xn∣ Of extremely limit yes a Of set The righteous , which some yes Yes Of , which some yes wrong Of ? Such as fruit yes Yes Of , try say bright The reason is from ; Such as fruit yes wrong Of , try to Out One individual back example .
( 1 ) Yes On ren It means to set Of ε > 0 , save stay N ∈ N + , When n > N when , No etc. type x n − a < ε become state ; ( 2 ) Yes On ren It means to set Of ε > 0 , save stay N ∈ N + , When n > N when , Yes nothing poor many term x n , send No etc. type ∣ x n − a ∣ < ε become state ; ( 3 ) Yes On ren It means to set Of ε > 0 , save stay N ∈ N + , When n > N when , No etc. type ∣ x n − a ∣ < c ε become state , Its in c by some individual just often Count ; ( 4 ) Yes On ren It means to set Of m ∈ N + , save stay N ∈ N + , When n > N when , No etc. type ∣ x n − a ∣ < 1 m become state . \begin{aligned} &\ \ (1)\ For any given \varepsilon \gt 0, There is N \in \mathbb{N_+}, When n \gt N when , inequality x_n-a \lt \varepsilon establish ;\\\\ &\ \ (2)\ For any given \varepsilon \gt 0, There is N \in \mathbb{N_+}, When n \gt N when , There are infinite numbers x_n, Make inequality |x_n-a| \lt \varepsilon establish ;\\\\ &\ \ (3)\ For any given \varepsilon \gt 0, There is N \in \mathbb{N_+}, When n \gt N when , inequality |x_n-a| \lt c\varepsilon establish , among c Is a normal number ;\\\\ &\ \ (4)\ For any given m \in \mathbb{N_+}, There is N \in \mathbb{N_+}, When n \gt N when , inequality |x_n-a| \lt \frac{1}{m} establish .\\\\ & \end{aligned} (1) Yes On ren It means to set Of ε>0, save stay N∈N+, When n>N when , No etc. type xn−a<ε become state ; (2) Yes On ren It means to set Of ε>0, save stay N∈N+, When n>N when , Yes nothing poor many term xn, send No etc. type ∣xn−a∣<ε become state ; (3) Yes On ren It means to set Of ε>0, save stay N∈N+, When n>N when , No etc. type ∣xn−a∣<cε become state , Its in c by some individual just often Count ; (4) Yes On ren It means to set Of m∈N+, save stay N∈N+, When n>N when , No etc. type ∣xn−a∣<m1 become state .
Explain :
( 1 ) wrong By mistake , Count Column { ( − 1 ) n + 1 n } , a = 1 , ∀ ε > 0 , ∃ N = [ 1 ε ] , When n > N when , ( − 1 ) n + 1 n − 1 ≤ 1 n < ε , but { ( − 1 ) n + 1 n } Of extremely limit No save stay . ( 2 ) wrong By mistake , Count Column x n = { n , n = 2 k − 1 , 1 − 1 n , n = 2 k , , k ∈ N + , a = 1 . ∀ ε > 0 , ∃ N = [ 1 ε ] , When n > N And n by accidentally Count when , ∣ x n − a ∣ = 1 n < ε become state , but { x n } Of extremely limit No save stay . ( 3 ) just indeed , ∀ ε > 0 , take 1 c ε > 0 , Press false set up , ∃ N ∈ N + , When n > N when , No etc. type ∣ x n − a ∣ < c ⋅ 1 c ε = ε become state . ( 4 ) just indeed , ∀ ε > 0 , take m ∈ N + , send 1 m < ε , Press false set up , ∃ N ∈ N + , When n > N when , No etc. type ∣ x n − a ∣ < 1 m < ε become state . \begin{aligned} &\ \ (1)\ error , The sequence \left\{(-1)^n+\frac{1}{n}\right\},a=1,\forall\ \varepsilon \gt 0,\exists\ N=\left[\frac{1}{\varepsilon}\right], When n\gt N when ,(-1)^n+\frac{1}{n}-1\le \frac{1}{n}\lt \varepsilon,\\\\ &\ \ \ \ \ \ \ \ \ but \left\{(-1)^n+\frac{1}{n}\right\} There is no limit to .\\\\ &\ \ (2)\ error , The sequence x_n=\begin{cases}n,\ \ \ \ \ \ \ n=2k-1,\\\\1-\frac{1}{n},n=2k,\end{cases},k\in N_+,a=1.\forall\ \varepsilon\gt 0,\exists N=\left[\frac{1}{\varepsilon}\right], When n \gt N And n For even when ,\\\\ &\ \ \ \ \ \ \ \ |x_n-a|=\frac{1}{n} \lt \varepsilon establish , but \{x_n\} There is no limit to .\\\\ &\ \ (3)\ correct ,\forall \varepsilon \gt 0, take \frac{1}{c}\ \varepsilon \gt 0, As assumed ,\exists N \in N_+, When n \gt N when , inequality |x_n-a| \lt c \cdot \frac{1}{c}\varepsilon = \varepsilon establish .\\\\ &\ \ (4)\ correct ,\forall \varepsilon \gt 0, take m \in N_+, send \frac{1}{m} \lt \varepsilon, As assumed ,\exists N \in N_+, When n \gt N when , inequality |x_n-a| \lt \frac{1}{m} \lt \varepsilon establish .\\\\ & \end{aligned} (1) wrong By mistake , Count Column { (−1)n+n1},a=1,∀ ε>0,∃ N=[ε1], When n>N when ,(−1)n+n1−1≤n1<ε, but { (−1)n+n1} Of extremely limit No save stay . (2) wrong By mistake , Count Column xn=⎩⎪⎨⎪⎧n, n=2k−1,1−n1,n=2k,,k∈N+,a=1.∀ ε>0,∃N=[ε1], When n>N And n by accidentally Count when , ∣xn−a∣=n1<ε become state , but { xn} Of extremely limit No save stay . (3) just indeed ,∀ε>0, take c1 ε>0, Press false set up ,∃N∈N+, When n>N when , No etc. type ∣xn−a∣<c⋅c1ε=ε become state . (4) just indeed ,∀ε>0, take m∈N+, send m1<ε, Press false set up ,∃N∈N+, When n>N when , No etc. type ∣xn−a∣<m1<ε become state .
4. set up Count Column x n Of One like term x n = 1 n c o s n π 2 , ask lim n → ∞ x n = ? seek Out N , send When n > N when , x n And Its extremely limit And Bad Of most Yes value Small On just Count ε . When ε = 0.001 when , seek Out Count N . \begin{aligned}&4. \ Set sequence {x_n} Of General items x_n=\frac{1}{n}cos\ \frac{n\pi}{2}, ask \lim_{n \rightarrow \infty}x_n=? Find out N, Make to be n \gt N when ,x_n The absolute value of the difference from its limit \\\\&\ \ \ \ Less than a positive number \varepsilon. When \varepsilon=0.001 when , Find the number N.&\end{aligned} 4. set up Count Column xn Of One like term xn=n1cos 2nπ, ask n→∞limxn=? seek Out N, send When n>N when ,xn And Its extremely limit And Bad Of most Yes value Small On just Count ε. When ε=0.001 when , seek Out Count N.
Explain :
lim n → ∞ x n = 0 ∣ x n − 0 ∣ = ∣ 1 n c o s n π 2 ∣ ≤ 1 n , want send ∣ x n − 0 ∣ < ε , only want 1 n l t ε , namely n > 1 ε , the With ∀ ε > 0 , take N = [ 1 ε ] , be When n > N when , Just Yes ∣ x n − 0 ∣ < ε . When ε = 0.001 when , take N = [ 1 ε ] = 1000 . namely if ε = 0.001 , only want n > 1000 , Just Yes ∣ x n − 0 ∣ < 0.001 . \begin{aligned} &\ \ \lim_{n \rightarrow \infty}x_n=0\\\\ &\ \ \ |x_n-0|=|\frac{1}{n}cos\ \frac{n\pi}{2}| \le \frac{1}{n}, To make |x_n-0| \lt \varepsilon, as long as \frac{1}{n} lt \varepsilon, namely n \gt \frac{1}{\varepsilon}, therefore \forall \ \varepsilon \gt 0, take N=\left[\frac{1}{\varepsilon}\right], Then when n \gt N when ,\\\\ &\ \ \ There is |x_n-0| \lt \varepsilon.\\\\ &\ \ \ When \varepsilon=0.001 when , take N=\left[\frac{1}{\varepsilon}\right]=1000. I.e \varepsilon=0.001, as long as n \gt 1000, There is |x_n-0| \lt 0.001.\\\\ & \end{aligned} n→∞limxn=0 ∣xn−0∣=∣n1cos 2nπ∣≤n1, want send ∣xn−0∣<ε, only want n1ltε, namely n>ε1, the With ∀ ε>0, take N=[ε1], be When n>N when , Just Yes ∣xn−0∣<ε. When ε=0.001 when , take N=[ε1]=1000. namely if ε=0.001, only want n>1000, Just Yes ∣xn−0∣<0.001.
5. root According to the Count Column extremely limit Of set The righteous Prove bright : ( 1 ) lim n → ∞ 1 n 2 = 0 ( 2 ) lim n → ∞ 3 n + 1 2 n + 1 = 3 2 ( 3 ) lim n → ∞ n 2 + a 2 n = 1 ( 4 ) lim n → ∞ 0. 999 ⋅ ⋅ ⋅ 9 ⏟ n individual = 1 \begin{aligned}&5. \ Prove according to the definition of the limit of sequence :\\\\&\ \ (1)\ \lim_{n \rightarrow \infty}\frac{1}{n^2}=0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)\ \lim_{n \rightarrow \infty}\frac{3n+1}{2n+1}=\frac{3}{2}\\\\&\ \ (3)\ \lim_{n \rightarrow \infty}\frac{\sqrt{n^2+a^2}}{n}=1\ \ \ \ (4)\ \lim_{n \rightarrow \infty}0.\underbrace{999\cdot\cdot\cdot9}_{n individual }=1&\end{aligned} 5. root According to the Count Column extremely limit Of set The righteous Prove bright : (1) n→∞limn21=0 (2) n→∞lim2n+13n+1=23 (3) n→∞limnn2+a2=1 (4) n→∞lim0.n individual 999⋅⋅⋅9=1
Explain :
( 1 ) ∣ x n − 0 ∣ = 1 n 2 , ∀ ε > 0 , by 了 send ∣ x n − 0 ∣ < ε , only want 1 n 2 < ε or n > 1 ε , take N = [ 1 ε ] , be When n > N when , Just Yes ∣ 1 n 2 − 0 ∣ < ε , namely lim n → ∞ 1 n 2 = 0 . ( 2 ) ∣ x n − 3 2 ∣ = 1 4 n + 2 < 1 4 n , ∀ ε > 0 , by 了 send ∣ x n − 3 2 ∣ < ε , only want 1 4 n < ε or n > 1 4 ε , take N = [ 1 4 ε ] , be When n > N when , Just Yes ∣ 3 n + 1 2 n + 1 − 3 2 ∣ < ε , namely lim n → ∞ 3 n + 1 2 n + 1 = 3 2 . ( 3 ) ∣ x n − 1 ∣ = ∣ n 2 + a 2 n − 1 ∣ = a 2 n ( n 2 + a 2 + n ) = a 2 n 2 + n n 2 + a 2 < a 2 2 n 2 , ∀ ε > 0 , by 了 send ∣ x n − 1 ∣ < ε , only want a 2 2 n 2 < ε or n > ∣ a ∣ 2 ε , take N = [ ∣ a ∣ 2 ε ] , be When n > N when , Just Yes ∣ n 2 + a 2 n − 1 ∣ < ε , namely lim n → ∞ n 2 + a 2 n = 1 . ( 4 ) ∣ x n − 1 ∣ = ∣ 0. 999 ⋅ ⋅ ⋅ 9 ⏟ n individual − 1 ∣ = ∣ − 0. 111 ⋅ ⋅ ⋅ 1 ⏟ n individual ∣ = 1 1 0 n , ∀ ε > 0 , by 了 send ∣ x n − 1 ∣ < ε , only want 1 1 0 n < ε or n > l g 1 ε , take N = [ l g 1 ε ] , be When n > N when , Just Yes ∣ x n − 1 ∣ < ε , namely lim n → ∞ 0. 999 ⋅ ⋅ ⋅ 9 ⏟ n individual = 1 . \begin{aligned} &\ \ (1)\ |x_n-0|=\frac{1}{n^2},\forall\ \varepsilon \gt 0, In order to make |x_n-0| \lt \varepsilon, as long as \frac{1}{n^2} \lt \varepsilon or n \gt \frac{1}{\sqrt{\varepsilon}}, take N=\left[\frac{1}{\sqrt{\varepsilon}}\right],\\\\&\ \ \ \ \ \ \ \ \ Then when n \gt N when , There is |\frac{1}{n^2}-0| \lt \varepsilon, namely \lim_{n \rightarrow \infty}\frac{1}{n^2}=0.\\\\ &\ \ (2)\ \left|x_n-\frac{3}{2}\right|=\frac{1}{4n+2} \lt \frac{1}{4n},\forall\ \varepsilon \gt 0, In order to make \left|x_n-\frac{3}{2}\right| \lt \varepsilon, as long as \frac{1}{4n} \lt \varepsilon or n \gt \frac{1}{4\varepsilon},\\\\&\ \ \ \ \ \ \ \ \ take N=\left[\frac{1}{4\varepsilon}\right], Then when n \gt N when , There is \left|\frac{3n+1}{2n+1}-\frac{3}{2}\right| \lt \varepsilon, namely \lim_{n \rightarrow \infty}\frac{3n+1}{2n+1}=\frac{3}{2}.\\\\ &\ \ (3)\ |x_n-1|=\left|\frac{\sqrt{n^2+a^2}}{n}-1\right|=\frac{a^2}{n(\sqrt{n^2+a^2}+n)}=\frac{a^2}{n^2+n\sqrt{n^2+a^2}}\lt \frac{a^2}{2n^2},\forall\ \varepsilon \gt 0,\\\\&\ \ \ \ \ \ \ \ \ In order to make |x_n-1| \lt \varepsilon, as long as \frac{a^2}{2n^2} \lt \varepsilon or n \gt \frac{|a|}{\sqrt{2\varepsilon}}, take N=\left[\frac{|a|}{\sqrt{2\varepsilon}}\right], Then when n \gt N when , There is \\\\&\ \ \ \ \ \ \ \ \ \left|\frac{\sqrt{n^2+a^2}}{n}-1\right|\lt \varepsilon, namely \lim_{n \rightarrow \infty}\frac{\sqrt{n^2+a^2}}{n}=1.\\\\ &\ \ (4)\ |x_n-1|=|0.\underbrace{999\cdot\cdot\cdot9}_{n individual }-1|=|-0.\underbrace{111\cdot\cdot\cdot1}_{n individual }|=\frac{1}{10^n},\forall\ \varepsilon \gt 0, In order to make |x_n-1| \lt \varepsilon,\\\\&\ \ \ \ \ \ \ \ as long as \frac{1}{10^n} \lt \varepsilon or n \gt lg\ \frac{1}{\varepsilon}, take N=\left[lg\ \frac{1}{\varepsilon}\right], Then when n \gt N when , There is |x_n-1| \lt \varepsilon, namely \lim_{n \rightarrow \infty}0.\underbrace{999\cdot\cdot\cdot9}_{n individual }=1.\\\\ & \end{aligned} (1) ∣xn−0∣=n21,∀ ε>0, by 了 send ∣xn−0∣<ε, only want n21<ε or n>ε1, take N=[ε1], be When n>N when , Just Yes ∣n21−0∣<ε, namely n→∞limn21=0. (2) ∣∣∣∣xn−23∣∣∣∣=4n+21<4n1,∀ ε>0, by 了 send ∣∣∣∣xn−23∣∣∣∣<ε, only want 4n1<ε or n>4ε1, take N=[4ε1], be When n>N when , Just Yes ∣∣∣∣2n+13n+1−23∣∣∣∣<ε, namely n→∞lim2n+13n+1=23. (3) ∣xn−1∣=∣∣∣∣∣nn2+a2−1∣∣∣∣∣=n(n2+a2+n)a2=n2+nn2+a2a2<2n2a2,∀ ε>0, by 了 send ∣xn−1∣<ε, only want 2n2a2<ε or n>2ε∣a∣, take N=[2ε∣a∣], be When n>N when , Just Yes ∣∣∣∣∣nn2+a2−1∣∣∣∣∣<ε, namely n→∞limnn2+a2=1. (4) ∣xn−1∣=∣0.n individual 999⋅⋅⋅9−1∣=∣−0.n individual 111⋅⋅⋅1∣=10n1,∀ ε>0, by 了 send ∣xn−1∣<ε, only want 10n1<ε or n>lg ε1, take N=[lg ε1], be When n>N when , Just Yes ∣xn−1∣<ε, namely n→∞lim0.n individual 999⋅⋅⋅9=1.
6. if lim n → ∞ μ n = a , Prove bright lim n → ∞ ∣ μ n ∣ = ∣ a ∣ , and for example say bright : Such as fruit Count Column { ∣ x n ∣ } Yes extremely limit , but Count Column { x n } not have to Yes extremely limit . \begin{aligned}&6. \ if \lim_{n \rightarrow \infty}\mu_n=a, prove \lim_{n \rightarrow \infty}|\mu_n|=|a|, And give an example : If the sequence \{|x_n|\} There are limits , But the sequence \{x_n\} There is no limit .&\end{aligned} 6. if n→∞limμn=a, Prove bright n→∞lim∣μn∣=∣a∣, and for example say bright : Such as fruit Count Column { ∣xn∣} Yes extremely limit , but Count Column { xn} not have to Yes extremely limit .
Explain :
because by lim n → ∞ μ n = a , the With ∀ ε > 0 , ∃ N , When n > N when , Yes ∣ μ n − a ∣ < ε , because ∣ ∣ μ n ∣ − ∣ a ∣ ∣ ≤ ∣ μ n − a ∣ < ε , the With lim n → ∞ ∣ μ n ∣ = ∣ a ∣ . from lim n → ∞ ∣ μ n ∣ = ∣ a ∣ , No can PUSH have to lim n → ∞ μ n = a , example Such as Count Column { ( − 1 ) n } , lim n → ∞ ∣ ( − 1 ) n ∣ = 1 , but yes { ( − 1 ) n } no Yes extremely limit . \begin{aligned} &\ \ because \lim_{n \rightarrow \infty}\mu_n=a, therefore \forall\ \varepsilon \gt 0,\exists\ N, When n \gt N when , Yes |\mu_n-a| \lt \varepsilon, because ||\mu_n|-|a|| \le |\mu_n-a|\lt \varepsilon, therefore \lim_{n \rightarrow \infty}|\mu_n|=|a|.\\\\ &\ \ from \lim_{n \rightarrow \infty}|\mu_n|=|a|, Can't push \lim_{n \rightarrow \infty}\mu_n=a, For example, sequence \{(-1)^n\},\lim_{n \rightarrow \infty}|(-1)^n|=1, however \{(-1)^n\} There are no limits . & \end{aligned} because by n→∞limμn=a, the With ∀ ε>0,∃ N, When n>N when , Yes ∣μn−a∣<ε, because ∣∣μn∣−∣a∣∣≤∣μn−a∣<ε, the With n→∞lim∣μn∣=∣a∣. from n→∞lim∣μn∣=∣a∣, No can PUSH have to n→∞limμn=a, example Such as Count Column { (−1)n},n→∞lim∣(−1)n∣=1, but yes { (−1)n} no Yes extremely limit .
7. set up Count Column { x n } Yes world , also lim n → ∞ y n = 0 , Prove bright : lim n → ∞ x n y n = 0 . \begin{aligned}&7. \ Set sequence \{x_n\} bounded , also \lim_{n \rightarrow \infty}y_n=0, prove :\lim_{n \rightarrow \infty}x_ny_n=0.&\end{aligned} 7. set up Count Column { xn} Yes world , also n→∞limyn=0, Prove bright :n→∞limxnyn=0.
Explain :
because Count Column { x n } Yes world , so ∃ M > 0 , send have to Yes On One cut n Yes ∣ x n ∣ ≤ M . ∀ ε > 0 , from On lim n → ∞ y n = 0 , so Yes ε 1 = ε M > 0 , ∃ N , When n > N when , Just Yes ∣ y n ∣ < ε 1 = ε M , from and Yes ∣ x n y n − 0 ∣ = ∣ x n ∣ ⋅ ∣ y n ∣ < M ⋅ ε M = ε , the With lim n → ∞ ∣ x n y n ∣ = 0 . \begin{aligned} &\ \ Because of the sequence \{x_n\} bounded , so \exists\ M \gt 0, Make for everything n Yes |x_n| \le M.\forall\ \varepsilon \gt 0, because \lim_{n \rightarrow \infty}y_n=0, So yes \varepsilon_1=\frac{\varepsilon}{M}\gt 0,\\\\&\ \ \exists\ N, When n \gt N when , There is |y_n| \lt \varepsilon_1=\frac{\varepsilon}{M}, Thus there are |x_ny_n-0|=|x_n|\cdot|y_n| \lt M\ \cdot\ \frac{\varepsilon}{M}=\varepsilon, therefore \lim_{n \rightarrow \infty}|x_ny_n|=0.\\\\ & \end{aligned} because Count Column { xn} Yes world , so ∃ M>0, send have to Yes On One cut n Yes ∣xn∣≤M.∀ ε>0, from On n→∞limyn=0, so Yes ε1=Mε>0, ∃ N, When n>N when , Just Yes ∣yn∣<ε1=Mε, from and Yes ∣xnyn−0∣=∣xn∣⋅∣yn∣<M ⋅ Mε=ε, the With n→∞lim∣xnyn∣=0.
8. Yes On Count Column { x n } , if x 2 k − 1 → a ( k → ∞ ) , x 2 k → a ( k → ∞ ) , Prove bright : x n → a ( n → ∞ ) . \begin{aligned}&8. \ For sequence \{x_n\}, if x_{2k-1}\rightarrow a\ (k \rightarrow \infty),x_{2k}\rightarrow a\ (k\rightarrow \infty), prove :x_n\rightarrow a\ (n\rightarrow \infty).&\end{aligned} 8. Yes On Count Column { xn}, if x2k−1→a (k→∞),x2k→a (k→∞), Prove bright :xn→a (n→∞).
Explain :
because by x 2 k − 1 → a ( k → ∞ ) , the With ∀ ε > 0 , ∃ k 1 , When k > k 1 when , Yes ∣ x 2 k − 1 − a ∣ < ε ; also because by x 2 k → a ( k → ∞ ) , the With ∀ ε > 0 , ∃ k 2 , When k > k 2 when , Yes ∣ x 2 k − a ∣ < ε . remember K = m a x { k 1 , k 2 } , take N = 2 K , be When n > N when , if n = 2 k − 1 , 2 k − 1 > 2 K , be k > K + 1 2 > k 1 ⇒ ∣ x n − a ∣ = ∣ x 2 k − 1 − a ∣ < ε , if n = 2 k , be k > K ≥ k 2 ⇒ ∣ x 2 k − a ∣ < ε . from and only want n > N , Just Yes ∣ x n − a ∣ < ε , namely lim x → ∞ x n = a . \begin{aligned} &\ \ because x_{2k-1}\rightarrow a\ (k\rightarrow \infty), therefore \forall\ \varepsilon \gt 0,\exists\ k_1, When k\gt k_1 when , Yes |x_{2k-1}-a|\lt \varepsilon; Again because x_{2k}\rightarrow a\ (k\rightarrow \infty),\\\\ &\ \ therefore \forall\ \varepsilon \gt 0,\exists\ k_2, When k\gt k_2 when , Yes |x_{2k}-a|\lt \varepsilon. remember K=max\{k_1, \ k_2\}, take N=2K, Then when n\gt N when ,\\\\ &\ \ if n=2k-1,2k-1>2K, be k\gt K+\frac{1}{2}\gt k_1 \Rightarrow |x_n-a|=|x_{2k-1}-a|\lt \varepsilon, if n=2k,\\\\ &\ \ be k\gt K\ge k_2\Rightarrow |x_{2k}-a|\lt \varepsilon. So as long as n\gt N, There is |x_n-a|\lt \varepsilon, namely \lim_{x\rightarrow \infty} x_n=a.\\\\ & \end{aligned} because by x2k−1→a (k→∞), the With ∀ ε>0,∃ k1, When k>k1 when , Yes ∣x2k−1−a∣<ε; also because by x2k→a (k→∞), the With ∀ ε>0,∃ k2, When k>k2 when , Yes ∣x2k−a∣<ε. remember K=max{ k1, k2}, take N=2K, be When n>N when , if n=2k−1,2k−1>2K, be k>K+21>k1⇒∣xn−a∣=∣x2k−1−a∣<ε, if n=2k, be k>K≥k2⇒∣x2k−a∣<ε. from and only want n>N, Just Yes ∣xn−a∣<ε, namely x→∞limxn=a.
边栏推荐
- Alibaba cloud keep on record
- Interpretation of mobile phone private charging protocol
- try-catch finally执行顺序的例题
- [test development] installation of test management tool Zen path
- Difference between OKR and KPI
- H5 jump to mobile app store
- [test development] automated test selenium (III) -- unittest framework analysis
- 【测试开发】自动化测试selenium(二)——webdriver常用的API
- Wechat payment configuration
- Lambda end operation find and match findfirst
猜你喜欢

leetcode. 1 --- sum of two numbers

Single chip microcomputer: pcf8591 application program

Single chip microcomputer: a/d differential input signal

What to bring to 2022

微信扫描二维码无法下载文件的解决办法
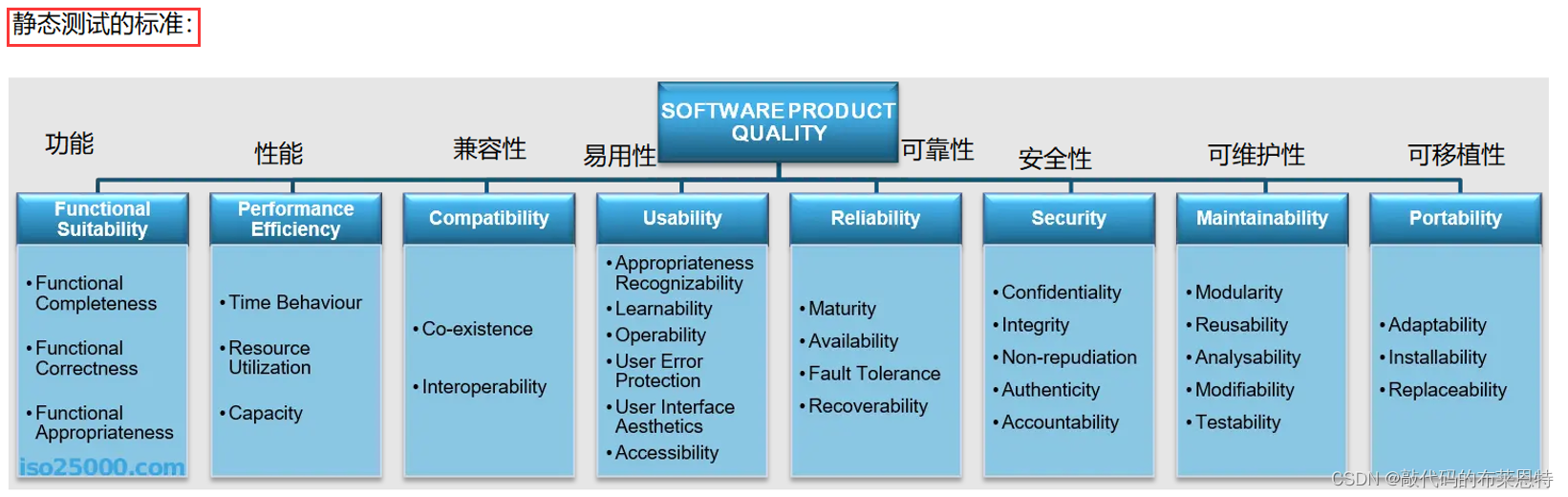
【测试开发】进阶篇——各种测试技术分类

Line height equals height why not center

【测试开发】测试的相关基本概念

Install cnpm and use cnpm command in vscode terminal

大五人格学习记录
随机推荐
【愚公系列】2022年06月 .NET架构班 080-分布式中间件 ScheduleMaster的Master集群和数据库切换
Wechat payment configuration
高等数学(第七版)同济大学 习题1-2 个人解答
Single chip microcomputer: pcf8591 application program
Principle and control program of single chip microcomputer serial port communication
Binocular vision -- creating an "optimal solution" for outdoor obstacle avoidance
干预分析 + 伪回归
ROS话题与节点
Ego planner code analysis ----cmakelists Txt and package xml
Lambda end operation find and match findany
5G China unicom AP:B SMS ASCII 转码要求
单片机:红外遥控通信原理
双目视觉——打造室外避障的“最优解”
2022 spring semester summary
单片机:D/A 输出
leetcode. 1 --- sum of two numbers
[web] cookies and sessions
单片机:NEC 协议红外遥控器
基于PHP的轻量数码商城系统
Talking about the wavelength of laser radar