当前位置:网站首页>二叉搜索树(搜索二叉树)模拟实现(有递归版本)
二叉搜索树(搜索二叉树)模拟实现(有递归版本)
2022-08-03 10:43:00 【韩悬子】
1.二叉搜索树概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树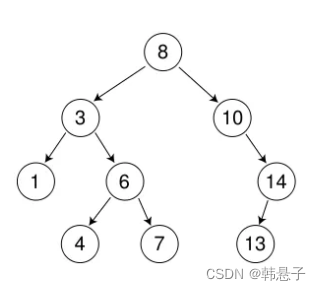
2.insert和find和InOrder实现
就讲一下insert怎么实现,分为二种情况,一种是二叉树为空,另一种不为空插入,第一种很好解决,第二种,因为要满足,搜索二叉树的要左子树要比跟小,右子树要比跟大,那么我们只要用插入的数和根比大小就好了,根小于插入的数就访问右边,根大于插入的数就访问左边,一直循环找到空节点为止,最后就是找到位置插入了,但是要插入的位置是左边还是右边不清楚,那么很简单记录这个节点的父亲节点再比较大小,比父亲节点小左边,比父亲节点大右边。
find这个也简单其实和insert一样访问到空节点就代表没找到,而找到了的情况是循环里面要查找的数,不小于或者大于根的左右树
#pragma once
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{
}
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
bool find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
bool insert(const K& key)
{
//为空的时候
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key < key)
{
parent->_right=cur;
}
else
{
parent->_left = cur;
}
return true;
}
void InOrder()
{
_InOrder(_root);
}
private:
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
Node* _root=nullptr;
};
void TestBSTree()
{
BSTree<int> t;
int a[] = {
8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
t.insert(e);
}
t.InOrder();
t.insert(16);
t.insert(9);
t.InOrder();
}
运行结果
3.erase实现
想删除肯定先遍历,删完分为
a. 要删除的结点无孩子结点
b. 要删除的结点只有一个孩子,左为空或右为空
d. 要删除的结点有左、右孩子结点
等情况来实现
只有一个孩子的情况下:要考虑要删除的节点是left还是right为空,并且还要考虑,可能是只有根左子树没有右子树的情况,或者是根右子树没有左子树的情况,毕竟原理是删除cur,让父亲节点的左边或者右边指向要删除节点的左边或者右边
有左右节点:让删除的节点和要删除节点的right中最小交换,或者覆盖,再把要删除的节点删除
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if(cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 一个孩子--左为空 or 右为空
// 两个孩子 -- 替换法
if (cur->_left == nullptr)
{
//if(cur==nullptr)
if (cur == _root)//没有左子树问题
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
//if(cur==nullptr)
if (cur == _root)//没有右子树的问题
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else//二个孩子都为空
{
// 右子树的最小节点替代
Node* minParent = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
minParent = minRight;
minRight = minRight->_left;
}
swap(minRight->_key, cur->_key);
if (minParent->_left == minRight)
{
minParent->_left = minRight->_right;
}
else
{
minParent->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false;
}
void TestBSTree1()
{
BSTree<int> t;
int a[] = {
8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
t.insert(e);
}
t.InOrder();
t.Erase(3);
t.Erase(8);
t.InOrder();
t.Erase(14);
t.Erase(7);
t.InOrder();
for (auto e : a)
{
t.Erase(e);
}
t.InOrder();
}
运行结果
4.构造赋值析构实现
// 强制编译器自己生成构造
// C++11
BSTree() = default;
BSTree(const BSTree<K>&t)
{
_root = CopyTree(t._root);
}
// t1 = t2
BSTree<K>& operator=(BSTree<K> t)
{
swap(_root, t._root);
return *this;
}
Node* CopyTree(Node* root)
{
if (root == nullptr)
return nullptr;
Node* copyNode = new Node(root->_key);
copyNode->_left = CopyTree(root->_left);
copyNode->_right = CopyTree(root->_right);
return copyNode;
}
~BSTree()
{
DestoryTree(_root);
_root = nullptr;
}
void DestoryTree(Node* root)
{
if (root == nullptr)
return;
DestoryTree(root->_left);
DestoryTree(root->_right);
delete root;
}
5.迭代查找
bool FindR(const K& key)
{
return _FindR(_root, key);
}
bool _FindR(Node* root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _FindR(root->_right, key);
}
else if (root->_key > key)
{
return _FindR(root->_left, key);
}
else
{
return true;
}
}
6.递归插入
加了引用的root就是父亲节点
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
return _InsertR(root->_right, key);
else if (root->_key > key)
return _InsertR(root->_left, key);
else
return false;
}
递归展开图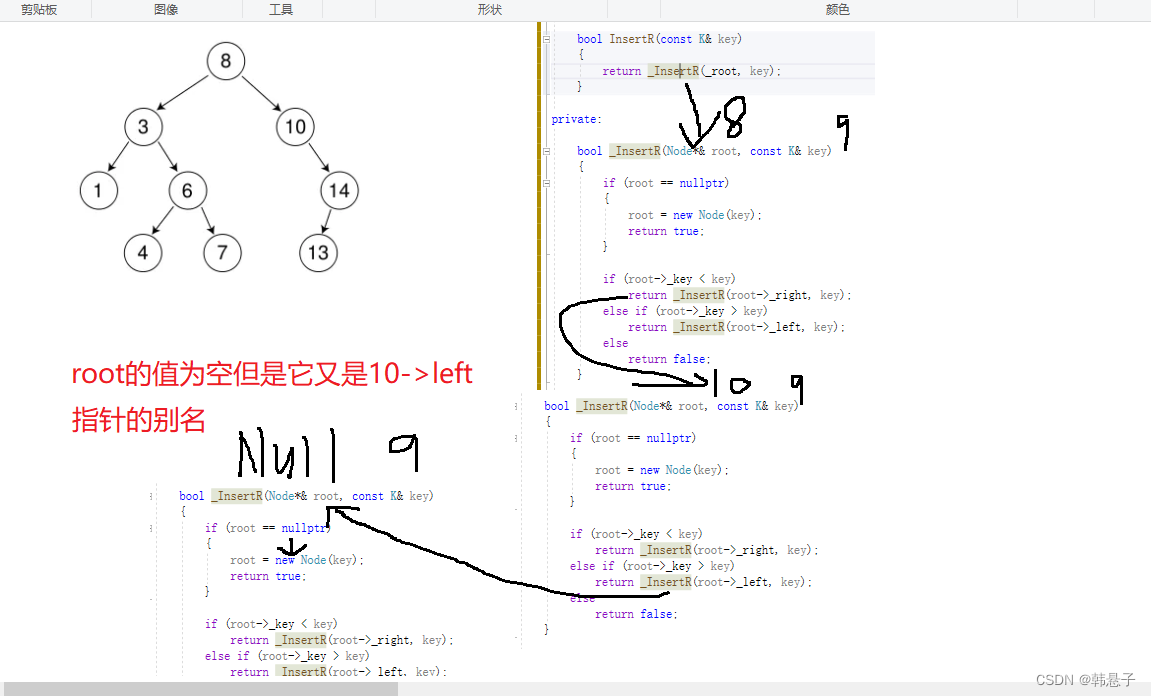
7.递归删除
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
Node* del = root;
// 删除
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
Node* minRight = root->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
swap(root->_key, minRight->_key);
return _EraseR(root->_right, key);
}
delete del;
return true;
}
}
8.搜索二叉树全部代码加递归写法
#pragma once
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{
}
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
// 强制编译器自己生成构造
// C++11
BSTree() = default;
BSTree(const BSTree<K>&t)
{
_root = CopyTree(t._root);
}
// t1 = t2
BSTree<K>& operator=(BSTree<K> t)
{
swap(_root, t._root);
return *this;
}
~BSTree()
{
DestoryTree(_root);
_root = nullptr;
}
bool find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
bool insert(const K& key)
{
//为空的时候
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if(cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 一个孩子--左为空 or 右为空
// 两个孩子 -- 替换法
if (cur->_left == nullptr)
{
//if(cur==nullptr)
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
//if(cur==nullptr)
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else//二个孩子都为空
{
// 右子树的最小节点替代
Node* minParent = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
minParent = minRight;
minRight = minRight->_left;
}
swap(minRight->_key, cur->_key);
if (minParent->_left == minRight)
{
minParent->_left = minRight->_right;
}
else
{
minParent->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
///
bool FindR(const K& key)
{
return _FindR(_root, key);
}
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
private:
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
Node* del = root;
// 删除
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
Node* minRight = root->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
swap(root->_key, minRight->_key);
return _EraseR(root->_right, key);
}
delete del;
return true;
}
}
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
return _InsertR(root->_right, key);
else if (root->_key > key)
return _InsertR(root->_left, key);
else
return false;
}
bool _FindR(Node* root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _FindR(root->_right, key);
}
else if (root->_key > key)
{
return _FindR(root->_left, key);
}
else
{
return true;
}
}
Node* CopyTree(Node* root)
{
if (root == nullptr)
return nullptr;
Node* copyNode = new Node(root->_key);
copyNode->_left = CopyTree(root->_left);
copyNode->_right = CopyTree(root->_right);
return copyNode;
}
void DestoryTree(Node* root)
{
if (root == nullptr)
return;
DestoryTree(root->_left);
DestoryTree(root->_right);
delete root;
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
Node* _root = nullptr;
};
void TestBSTree()
{
BSTree<int> t;
int a[] = {
8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
t.insert(e);
}
t.InOrder();
t.insert(16);
t.insert(9);
t.InOrder();
t.Erase(8);
for (auto e : a)
{
t.insert(e);
}
}
void TestBSTree1()
{
BSTree<int> t;
int a[] = {
8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
t.insert(e);
}
t.InOrder();
t.Erase(3);
t.Erase(8);
t.InOrder();
t.Erase(14);
t.Erase(7);
t.InOrder();
for (auto e : a)
{
t.Erase(e);
}
t.InOrder();
}
void TestBSTree4()
{
BSTree<int> t;
int a[] = {
8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
t.insert(e);
}
t.InOrder();
BSTree<int> copy = t;
copy.InOrder();
}
边栏推荐
猜你喜欢
随机推荐
C# Color颜色RGB对照表、颜色选择器
GBase 8c与openGauss是什么关系?
MATLAB程序设计与应用 2.6 字符串
mysql数据库定时备份占用大量线程,导致全局锁表,有啥好的解决方法么
QSplitter(分离部件)
Mysql 主从复制 作用和原理
几款永久免费内网穿透,好用且简单_内网穿透平台
Mysql OCP 74 questions
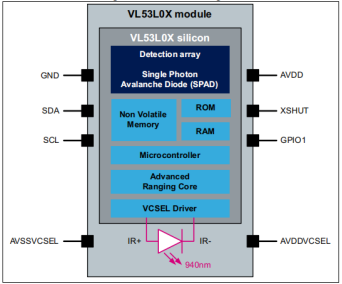
VL53L0X V2 laser ranging sensor collects distance data serial output
Who is more popular for hybrid products, depending on technology or market?
RecyclerView的item高度自适应
全新的Uber App设计
分辨率_分辨率越高越好?手机屏幕分辨率多少才合适?现在终于搞清楚了[通俗易懂]
Interview Blitz 71: What's the difference between GET and POST?
浪潮—英伟达打造元宇宙新方案,虚拟人的故事将再破你的认知
如何改变sys_guid() 返回值类型
月薪没到35K的程序员必须要背的面试八股,我先啃为敬!
SAP 电商云 Spartacus UI 的 External Routes 设计明细
57.【全排列的详细分析】
阿里本地生活全域日志平台 Xlog 的思考与实践