Three elements of basic concepts and methods of machine learning

Purpose of the course

• Understand the principle
• Tools can be used to solve practical problems
• Use programming language to implement algorithms
• Improve the ability to optimize and improve algorithms

Learning goals

• Understand concepts related to machine learning
• Understand the essence of machine learning
• Learn about common loss functions
• Understand the empirical and structural risks

---

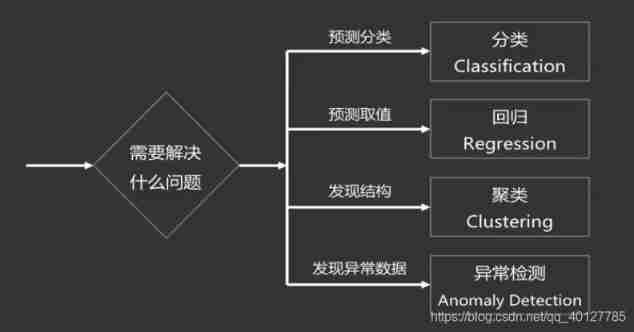
Some basic concepts of machine learning

Machine learning method flow

Take supervised learning as an example ,（ Compare examples to do exercises ）

input data ——》 Feature Engineering 《——》 model training ——》 Model deployment ——》 Model application

Model (Models)： A process formed through extensive experience

Feature Engineering (Features)： On the basis of input data , Arrangement 、 machining 、 Expand 、 Some new data features formed by merging, etc .

The modeling process is an iterative process , Loop optimization required .

After the model training reaches the expected effect, deploy it , Put it into practice .

notes ： In the actual work process , Business 、 The data is changing dynamically , So the model has timeliness , Model lifecycle management is required in the process of use , Regular updates .

Input space and output space

• input space ： The set of input values is called input space
• Output space ： The set of all possible values of the output is called the output space
  • The input space and output space can be a set of finite elements , It can also be the whole Euclidean space
  • The input space and output space can be a continuous set of values , It can also be a set of discrete values
  • Input space and output space can be the same space , It can also be different spaces
  • Usually the output space is smaller than the input space

The feature space

features ： The property . Each component of each input strength ( attribute ) Called original features , More derived features can be extended based on the original features .

Eigenvector ： A collection composed of multiple features , It is called eigenvector

The feature space ： The space where the eigenvector exists is called the eigenspace .

-   Each dimension in the feature space corresponds to a feature ( attribute )
-   The feature space can be the same as the input space , It can be different 
-   The instance needs to be mapped from the input space to the feature space 
-   The model is actually defined on the feature space 

Hypothetical space

Hypothetical space ： A set of mappings from input space to output space .

• Mr. Li Hang 《 Statistical learning method 》： The model belongs to an implicit set from input space to output space , This set is the hypothetical space . The determination of hypothesis space means the determination of learning range .
• zhou 《 machine learning 》： Hypothetical space refers to the space composed of all assumptions of the problem , We can think of the learning process as a process of searching in the hypothesis space , The search target is to find the training set “ matching ” Assumptions .

For every possible input , Can find a mapping , Corresponds to an output in the output space .

---

The essence of machine learning

Most machine learning is essentially an optimization problem , That is to find the model parameters （ Optimization variables ）, Make the loss function （ Objective function ） Minimum , At the same time, in order to avoid over fitting , Add regular terms , That is, constrain the parameters to be optimized . Deep learning is a branch of machine learning , It is used for classification , It is also an optimization problem . The general optimization problem is not easy to solve , Because it is easy to fall into the local optimal solution , And can not get the global optimum . If this optimization problem happens to be a convex optimization problem , Then the optimal solution of the model can be solved efficiently , This is because , According to the properties of convex functions , The local optimum is the global optimum .

---

Three elements of machine learning methods

Machine learning methods are usually made up of models 、 Strategy and algorithm are composed of three parts ：
Method = Model + Strategy + Algorithm

• Model ： Mapping from input space to output space . The learning process is to search the hypothesis space suitable for the current data .
• Strategy ： Learning criteria or rules for selecting the optimal model from a large number of assumptions in the hypothesis space
• Algorithm ： The specific calculation method of the learning model , The same is to solve the optimization problem

Model

Mapping from input space to output space . The learning process is to search the hypothesis space suitable for the current data .

Analyze current problems to be solved , Determine the model .

Strategy

Learning criteria or rules for selecting the optimal model from a large number of assumptions in the hypothesis space .

Choose the most appropriate model from the hypothetical space , The following problems need to be solved ：

• Evaluate the effect of a model on a single training sample
• Evaluate the overall effect of a model on the training set
• Evaluate a model pair, including a training set 、 The overall effect of all data including the prediction set

Define several indicators to measure the above problems ：

• Loss function ：0-1 Loss function 、 Square loss function 、 Absolute loss function 、 Logarithmic loss function, etc ;
• Risk function ： Empirical risk 、 Expected risk 、 Structural risk

Basic strategy ：

• Experience risk is minimal (EMR：Empirical Risk Minimization)
• Minimum structural risk (SRM：Structural Risk Minimization)

Loss function

Loss function ： Used to measure the gap between the predicted results and the real results , The less it's worth , It means that the more consistent the predicted results are with the real results . It's usually a non negative real valued function . The process of reducing the loss function in various ways is called optimization . The loss function is recorded as L(Y,f(x))

Common loss function types ：

• 0-1 Loss function (0-1LF)： If the predicted value is exactly equal to the actual value, then “ No loss ” by 0, Otherwise it means “ Total loss ”, by 1.

  The predicted value and the actual value are exactly equal, which is a little too strict , You can use the method that the difference between the two is less than a certain threshold .

• Absolute loss function ： The absolute value of the difference between the predicted result and the real result . Simple and easy to understand , But the calculation is inconvenient ;

• Square loss function ： The square of the difference between the predicted result and the real result .

  • The advantages of the square loss function are ：
    • The error of each sample is positive , The accumulation will not be offset ;
    • The penalty of square for large error is greater than that of small error
    • Simple mathematical calculation 、 friendly , The derivative is a first-order function

• Logarithmic loss function ( Log likelihood loss function )： Logarithmic functions are monotonic , When solving optimization problems , The result is consistent with the original goal . You can convert multiplication into addition ( A simpler calculation ), simplified calculation ：L(Y,p(Y|X)) = -logP(Y|X)

• Exponential loss function ： monotonicity 、 Excellent properties of nonnegativity , Make the closer to the correct result, the smaller the error ;

• Folding loss function ： Also known as hinge loss , The punishment for the points near the judgment boundary is high , Commonly used in SVM( Support vector machine ),L(f(x)) = max(0,1 - f(x))

• The curves of different loss functions are also different
  

• Different loss functions have different characteristics , For different scenarios ：

  • 0-1： Ideal state model
  • log： Logical regression 、 Cross entropy
  • Squared： Linear regression
  • Exponential：AdaBoosting
  • Hinge：SVM、soft margin

Empirical risk and structural risk

Empirical risk VS Risk function

Empirical risk ： The loss function measures the prediction results of a single sample , To measure the difference between the predicted value and the real value of the whole training set , Make a prediction for all records of a real training set , Take the loss function , Add up all values , Experience risk . Empirical risk model f(x) The better the fitting degree of the training set .

Risk function ： Also known as expected loss 、 Expected risk . All data sets ( Contains training set and prediction set , Follow joint distribution P(X,Y)) The expected value of the loss function .

• Empirical risk vs Expected risk

  • Expect the letter to be model to global ( All data sets ) The effect of ; Empirical risk is the impact of the model on the Bureau ( Training set ) The effect of ;
  • The expected risk is often incalculable , Joint distribution P(X,Y) Usually unknown ; Empirical risk can be calculated ;
  • When the training set is large enough , Empirical risk can replace expected risk , That is, the local optimum replaces the global optimum

• The problem of experience risk ：

  • When the sample is small , Focus only on experience risk , It can easily lead to over fitting

    * namely ： Using samples to calculate empirical risk , When forecasting a forecast set , The empirical risk is too close to the sample set , The prediction error rate of the prediction set is higher . The empirical risk obtained is only a local optimal solution .

resolvent ：

Structural risk

Structural risk ： On the basis of experience and risk , Add a regularization term or penalty term .

Structural risk vs Empirical risk

• The less experience risk , The more complex the model decision function , The more parameters it contains
• When the empirical risk function is small to a certain extent, there will be over fitting phenomenon
• Ways to prevent overfitting , It is necessary to reduce the complexity of the decision function , Let the punishment J(f) To minimize the
• It is necessary to minimize the complexity of both empirical risk function and model decision function
• The structural risk function is obtained by fusing the two formulas into one formula, and then the structural risk function is minimized .

Regularization term

Regularization term ： Penalty function , This item penalizes the model vector , Thus the problem of over fitting is solved . The regularization method will automatically weaken the unimportant characteristic variables , Automatically from many characteristic variables “ extract ” Important characteristic variables , Reduce the order of magnitude of the characteristic variable .

summary

1. Some basic concepts of machine learning

2. The essence of machine learning ,

   • A hypothesis is searched in the hypothesis space from input space to output space , Choose the best hypothesis for the current treatment .

3. Three elements of machine learning

   • Model ： Determine what kind of problems
   • Strategy ： How to evaluate the model
   • Algorithm ： How to optimize and improve within the scope required by the learning rules , Get the results you want

4. Empirical risk and structural risk

   Use when dealing with the strategy of the three elements , In fact, the way to judge whether the model is good or bad , Structural risk is often used to assess

   • The difference between structural risk and empirical risk
     • Empirical risk only evaluates the performance of the model on the test set , The better on the test set , The less experience risk
     • Structural risk should be considered in both aspects ：1. The model performs well on the test set ;2. The complexity of the model is not high , The more complex the model , The worse the prediction effect on the follow-up , Easy to overfit

Optimize and improve within the scope required by the learning rules , Get the results you want

4. Empirical risk and structural risk

   Use when dealing with the strategy of the three elements , In fact, the way to judge whether the model is good or bad , Structural risk is often used to assess

   • The difference between structural risk and empirical risk
     • Empirical risk only evaluates the performance of the model on the test set , The better on the test set , The less experience risk
     • Structural risk should be considered in both aspects ：1. The model performs well on the test set ;2. The complexity of the model is not high , The more complex the model , The worse the prediction effect on the follow-up , Easy to overfit