当前位置：网站首页>漫画：有趣的 “切蛋糕“ 问题

漫画：有趣的 “切蛋糕“ 问题

2022-06-11 14:06:00 【大数据v】

导读：一道又烧脑又有趣的ACM比赛题目。

作者：小灰

来源：程序员小灰（ID：chengxuyuanxiaohui）

————— 第二天 —————

举个例子：

我们有5块蛋糕，蛋糕的大小分别是 5，17，25，3，15

我们有7位顾客，他们的饭量分别是 2，5，7，9，12，14，20

（每个蛋糕大小和顾客食量都是小于1000的整数，蛋糕和顾客的数量不超过1000）

在分发蛋糕时，有一个特殊的规则：蛋糕可分不可合。

什么意思呢？

一块较大的蛋糕，可以切分成多个小块，用来满足多个胃口较小的顾客：

但是，若干块较小的蛋糕，不允许合并成一块大蛋糕，用来满足一个胃口较大的顾客：

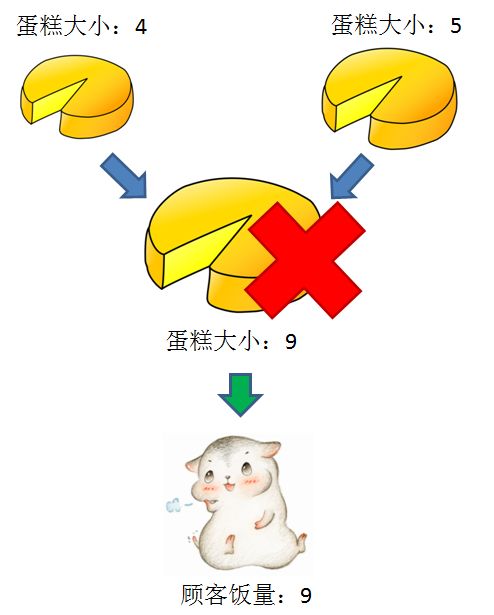
最后的问题是：给定蛋糕大小的集合cakes，给定顾客饭量的集合mouths，如何计算出这些蛋糕可以满足的最大顾客数量？

比如：输入cakes集合 {2，9}；输入mouths集合 {5，4， 2，8}
正确返回：3

小灰的思路：

为了让更多的顾客吃饱，肯定要优先满足食量小的顾客，所以小灰决定使用贪心算法。

首先，把蛋糕和顾客从小到大进行排序：

按照上面的例子，排序结果如下：

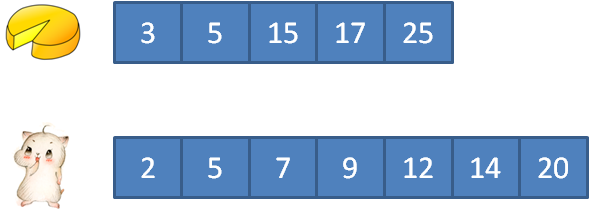
接下来，让每一个蛋糕和顾客按照从左到右的顺序匹配。如果蛋糕大于顾客饭量，则切分蛋糕；如果蛋糕小于顾客饭量，则丢弃该蛋糕。

第1块蛋糕大小是3，第1个顾客饭量是2，于是把蛋糕切分成2+1，满足顾客。剩下的1大小蛋糕无法满足下一位顾客，丢弃掉。

第2块蛋糕大小是5，第2个顾客饭量是5，刚好满足顾客。

第3块蛋糕大小是15，第3个顾客饭量是7，于是把蛋糕切分成7+8，满足顾客。剩下的8大小蛋糕无法满足下一位顾客，丢弃掉。

第4块蛋糕大小是17，第4个顾客饭量是9，于是把蛋糕切分成9+8，满足顾客。剩下的8大小蛋糕无法满足下一位顾客，丢弃掉。

第5块蛋糕大小是25，第5个顾客饭量是12，于是把蛋糕切分成12+13，满足顾客。剩下的13大小蛋糕无法满足下一位顾客，丢弃掉。

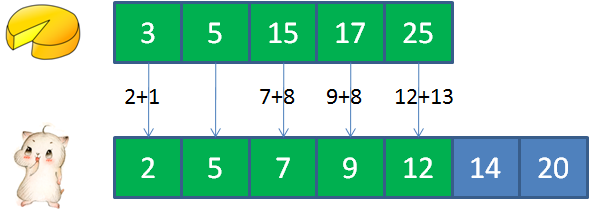
这样一来，所有蛋糕都用完了，由贪心算法得出结论，最大能满足的顾客数量是5。

例子当中：

3的蛋糕满足2的顾客，
5的蛋糕满足5的顾客，
15的蛋糕满足12的顾客，
17的蛋糕满足7和9的顾客，
25的蛋糕满足14的顾客。

显然，面试官随意给出的吃法，满足了6个顾客。

————————————

这句话听起来有点绕，什么意思呢？我们可以看看下面这张图：

其实道理很简单，由于顾客的饭量是从小到大排序的，优先满足饭量小的顾客，才能尽量满足更多的人。

因此，在记录顾客饭量的数组中，必定存在一段从最左侧开始的连续元素，符合当前蛋糕所能满足的最多顾客组合。

这样一来，我们的题目就从寻找最大满足顾客数量，转化成了寻找顾客饭量有序数组中的最大满足临界点：

让我们先来回顾一下二分查找的思路：

1. 选择中间元素，下标mid = （0 + 6）/2 = 3 ，因此中间元素是9：

2. 判断9>5，选择元素9左侧部分的中间元素，下标mid = （0+2）/2 = 1，因此中间元素是5：

3. 判断5=5，查找结束。

但是，切蛋糕的问题比普通的二分查找要复杂得多，因为我们要寻找的顾客饭量数组临界元素，并不是简单地判断元素是否相等，而是要验证给定的蛋糕能否满足临界元素之前的所有顾客。

如何来实现呢？我们仍旧使用刚才的例子，演示一下详细过程：

第一步，寻找顾客数组的中间元素。

在这里，中间元素是9：

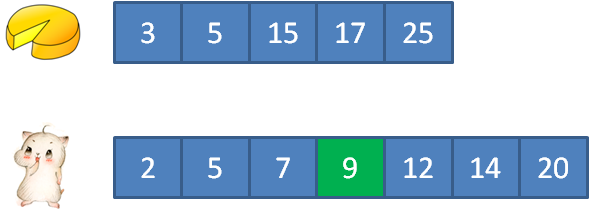
第二步，验证饭量从2到9的顾客能否满足。

子步骤1，遍历蛋糕数组，寻找大于9的蛋糕，最终寻找到元素15。

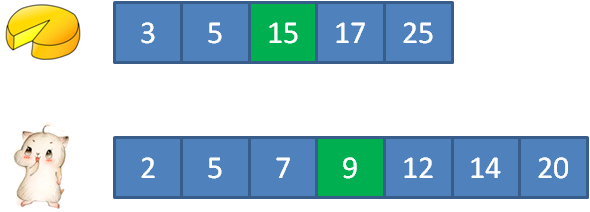
子步骤2，饭量9的顾客吃掉15的蛋糕，还剩6大小。

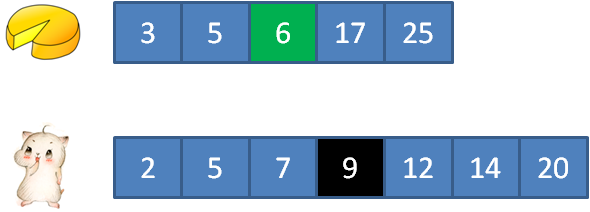
子步骤3，重新遍历蛋糕数组，寻找大于7的蛋糕，最终寻找到元素17。

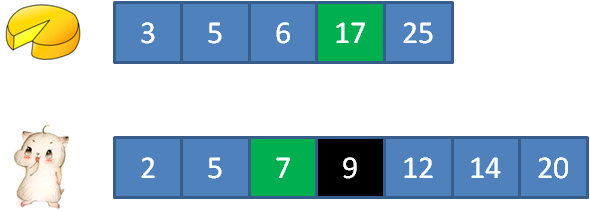
子步骤4，饭量7的顾客吃掉17的蛋糕，还剩10大小。

子步骤5，重新遍历蛋糕数组，寻找大于5的蛋糕，最终寻找到元素5。

子步骤6，饭量5的顾客吃掉5的蛋糕，还剩0大小。

子步骤7，重新遍历蛋糕数组，寻找大于2的蛋糕，最终寻找到元素3。

子步骤8，饭量2的顾客吃掉3的蛋糕，还剩1大小。

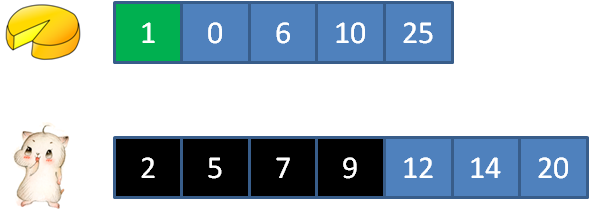
到此为止，从2到9的所有顾客都被满足了，验证成功。

接下来，我们需要引入更多顾客，从而试探出蛋糕满足的顾客上限。

第三步，重新寻找顾客数组的中间元素。

由于第二步验证成功，所以我们要在元素9右侧的区域，重新寻找中间元素。显然，这个中间元素是14：

第四步，验证饭量从2到14的顾客能否满足。

这一步和第二步的思路是相同的，这里就不详细阐述了。最终的验证结果是，从2到14的顾客能够满足。

接下来，我们还要引入更多顾客，试探出蛋糕满足的顾客上限。

第五步，重新寻找顾客数组的中间元素。

由于第四步验证成功，所以我们要在元素14右侧的区域，重新寻找中间元素。显然，这个中间元素也就是唯一的元素20：

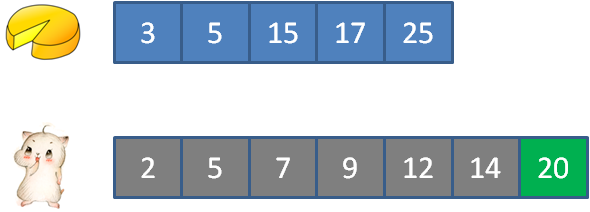
第六步，验证饭量从2到20的顾客能否满足。

这一步和第二步、第四步的思路是相同的，这里就不详细阐述了。最终的验证结果是，从2到20的顾客不能够满足。

经过以上步骤，我们找到了最大满足顾客的临界点14，从2到14共有6个顾客，所以给定蛋糕最大能满足的顾客数量是6。

//剩余蛋糕数量
static int leftCakes[];
//蛋糕总量（不是数量，而是大小之和）
static int totalCake = 0;
//浪费蛋糕量
static int lostCake = 0;
static boolean canFeed(int[] mouths, int monthIndex, int sum)
{
   if(monthIndex<=0) {
       //递归边界
       return true;
   }
   //如果 蛋糕总量-浪费蛋糕量 小于当前的需求量，直接返回false，即无法满足
   if(totalCake - lostCake < sum) {
       return false;
   }
   //从小到大遍历蛋糕
   for(int i=0;i<leftCakes.length; i++) {
       if (leftCakes[i] >= mouths[monthIndex]) {
           //找到并吃掉匹配的蛋糕
           leftCakes[i] -= mouths[monthIndex];
           //剩余蛋糕小于最小的需求，变为浪费蛋糕
           if (leftCakes[i] < mouths[1]){
               lostCake += leftCakes[i];
           }
           //继续递归，试图满足mid下标之前的需求
           if (canFeed(mouths, monthIndex-1, sum)) {
               return true;
           }
           //无法满足需求，蛋糕状态回滚
           if (leftCakes[i] < mouths[1]) {
               lostCake -= leftCakes[i];
           }
           leftCakes[i] += mouths[monthIndex];
       }
   }
   return false;
}
public static int findMaxFeed(int[] cakes, int[] mouths){
   //蛋糕升序排列，并把0下标空出
   int[] cakesTemp = Arrays.copyOf(cakes, cakes.length+1);
   Arrays.sort(cakesTemp);
   for(int cake: cakesTemp){
       totalCake += cake;
   }
   //顾客胃口升序排列，并把0下标空出
   int[] mouthsTemp = Arrays.copyOf(mouths, mouths.length+1);
   Arrays.sort(mouthsTemp);
   leftCakes = new int[cakes.length+1];
   //需求之和（下标0的元素是0个人的需求之和，下标1的元素是第1个人的需求之和，下标2的元素是第1,2个人的需求之和.....）
   int[] sum = new int[mouths.length+1];
   for(int i=1;i<=mouths.length;i++) {
       sum[i] = sum[i - 1] + mouthsTemp[i];
   }
   //left和right用于计算二分查找的“中点”
   int left=1,right=mouths.length;
   //如果胃口总量大于蛋糕总量，right指针左移
   while(sum[right]> totalCake){
       right--;
   }
   //中位指针，用于做二分查找
   int mid=((left+right)>>1);
   while(left<=right)
   {
       //重置剩余蛋糕数组
       leftCakes = Arrays.copyOf(cakesTemp, cakesTemp.length);
       //重置浪费蛋糕量
       lostCake =0;
       //递归寻找满足需求的临界点
       if(canFeed(mouthsTemp, mid, sum[mid])){
           left=mid+1;
       } else {
           right = mid - 1;
       }
       mid=((left+right)>>1);
   }
   //最终找到的是刚好满足的临界点
   return mid;
}
public static void main(String[] args) {
   int[] cakes = new int[]{3,5,15,17,25};
   int[] mouths = new int[]{2,5,7,9,12,14,20};
   int maxFeed = findMaxFeed(cakes, mouths);
   System.out.println("最大满足顾客数：" + maxFeed);
}

这段代码比较复杂，需要说明几点：