当前位置:网站首页>机械臂速成小指南(十五):线性规划
机械臂速成小指南(十五):线性规划
2022-08-02 15:10:00 【躺躺我啊】
🥰🥳需要机械臂相关资源的同学可以在评论区中留言哦
指南目录:
🦾🪐以下为正文🦾🪐
上一章节中我们讨论了多项式插值轨迹规划,本章,我们讨论一种更为简单的关节空间轨迹规划方法:线性规划。
一、理论分析
顾名思义,线性规划中的“线性”,指的是机械臂的关节变量以恒定的速率变化,即关节的角速度恒定,如下图所示。
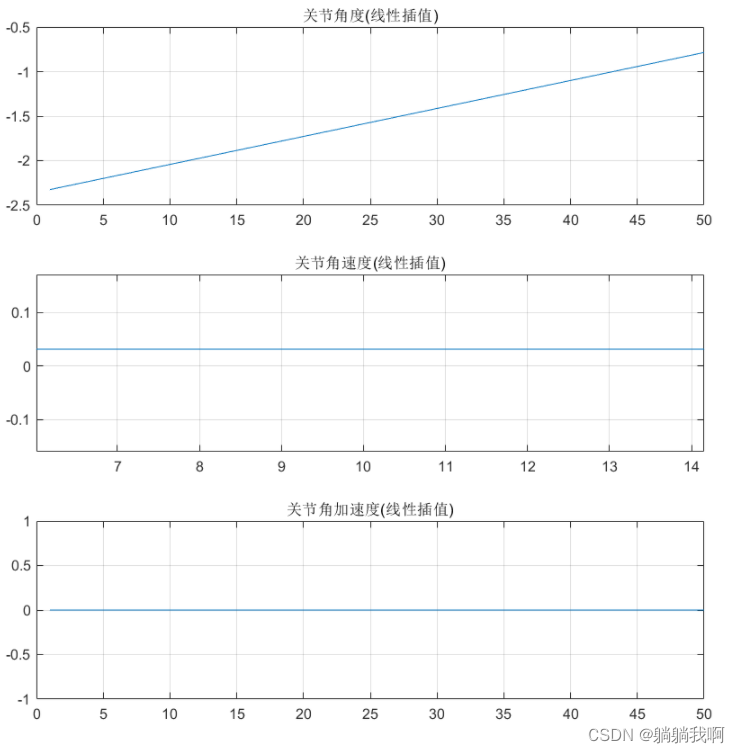
这种插值方法是在关节空间中简单地插入一个经过起点(t_0,θ_0) 与终点(t_f,θ_f) 的线段。令t_0=0 ,该线段可表示为
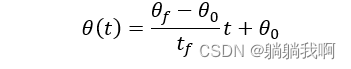
二、程序仿真
我们使用MATLAB对线性插值的轨迹规划方法进行仿真,并选取选择空间中一点(-100, -100,300,0,0,0 )作为轨迹规划的起点,而(200,-200,400,0,0,0)作为轨迹规划的终点。
首先,定义六自由度机械臂的DH参数。
lim1_min = -170 * radian1; lim1_max = 170 * radian1; %关节1(-170,170)
lim2_min = -132 * radian1; lim2_max = 0 * radian1; %关节2(-132,0)
lim3_min = 1 * radian1; lim3_max = 141 * radian1; %关节3(1,141)
lim4_min = -165 * radian1; lim4_max = 165 * radian1; %关节4(-165,165)
lim5_min = -105 * radian1; lim5_max = 105 * radian1; %关节5(-105,105)
lim6_min = -155 * radian1; lim6_max = 155 * radian1; %关节6(-155,155)
lim1 = lim1_max - lim1_min;
lim2 = lim2_max - lim2_min;
lim3 = lim3_max - lim3_min;
lim4 = lim4_max - lim4_min;
lim5 = lim5_max - lim5_min;
lim6 = lim6_max - lim6_min;
theta1 = 0; d1 = 169.77; a1 = 64.2; alpha1 = -pi/2; offset1 = 0;
theta2 = 0; d2 = 0; a2 = 305; alpha2 = 0; offset2 = 0;
theta3 = 0; d3 = 0; a3 = 0; alpha3 = pi/2; offset3 = pi/2;
theta4 = 0; d4 = -222.63; a4 = 0; alpha4 = -pi/2; offset4 = 0;
theta5 = 0; d5 = 0; a5 = 0; alpha5 = pi/2; offset5 = 0;
theta6 = 0; d6 = -36.25; a6 = 0; alpha6 = 0; offset6 = -pi;第二步,运动学建模。
L(1) = Link([theta1, d1, a1, alpha1, offset1], 'standard');
L(2) = Link([theta2, d2, a2, alpha2, offset2], 'standard');
L(3) = Link([theta3, d3, a3, alpha3, offset3], 'standard');
L(4) = Link([theta4, d4, a4, alpha4, offset4], 'standard');
L(5) = Link([theta5, d5, a5, alpha5, offset5], 'standard');
L(6) = Link([theta6, d6, a6, alpha6, offset6], 'standard');
% 定义关节范围
L(1).qlim=[lim1_min,lim1_max];
L(2).qlim=[lim2_min,lim2_max];
L(3).qlim=[lim3_min,lim3_max];
L(4).qlim=[lim4_min,lim4_max];
L(5).qlim=[lim5_min,lim5_max];
L(6).qlim=[lim6_min,lim6_max];
robot = SerialLink(L,'name','AR3');第三步,定义起始点与终止点。
T1=transl(-100,-100,300); %齐次变换矩阵
T2=transl(200,-200,400); %齐次变换矩阵
init_ang=robot.ikine(T1); %运动学逆解
targ_ang=robot.ikine(T2); %运动学逆解第四步,定义储存机械臂关节旋转角度、角速度及角加速度的数组。
q = zeros(step,N); %初始化机械臂的位置
qd = zeros(step,N); %初始化机械臂的角速度
qdd = zeros(step,N); %初始化机械臂的角加速度第五步,按照上述原理进行线性插值。
step = 50
for t = 1:step
q(t,:) = (targ_ang-init_ang)/step * t + init_ang; %位置
qd(t,:) = (targ_ang-init_ang)/step; %角速度
qdd(t,:) = 0; %角加速度
end
T=robot.fkine(q); %运动学正解
nT=T.T; %转为齐次比那换矩阵
plot3(squeeze(nT(1,4,:)),squeeze(nT(2,4,:)),squeeze(nT(3,4,:)));%输出末端轨迹
title('线性插值轨迹');
robot.plot(q); %动画演示 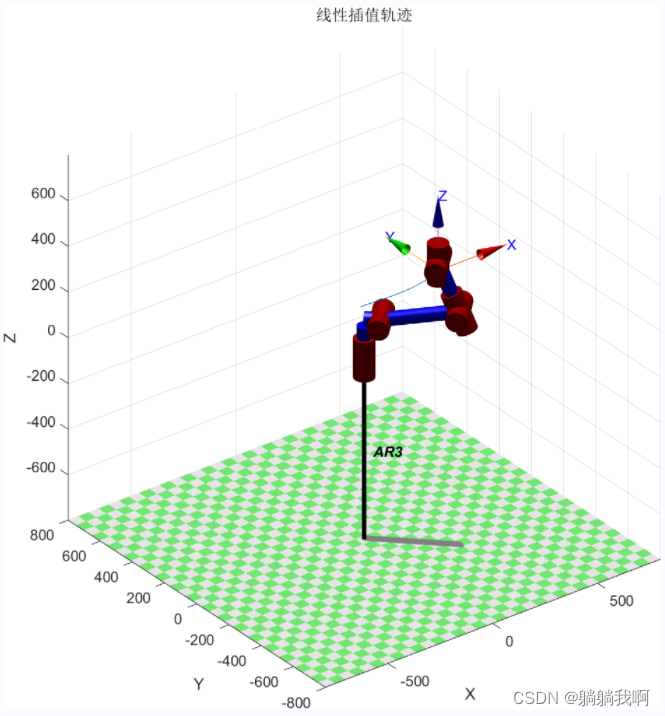 |  |
不难发现,虽然各个关节是以恒定的角速度旋转的,但末端执行器在空间中的轨迹并不是直线。
三、编程实现
具体的代码与多项式插值轨迹规划那一章中的代码类似,无非就是生成轨迹点的插值函数换成了这个线性的函数。

这种轨迹规划方法很简便,但是存在一个问题:我们将机械臂在起始点与终止点处的速度视为零,这就导致了机械臂在这两个位置会有速度的突变,则会对关节产生冲击,不利于机械臂的作业精度以及其臂体的坚固性,这一点在机械臂作两点间往复运动时尤为明显。
因此,由抛物线过渡的线性规划应运而生,我们会在下一章对其进行介绍。
边栏推荐
猜你喜欢
随机推荐
阿里云上安装MQTT服务器
MySQL的简单运用-where、update、delete、like、union
Reed-Solomon Codes——RS纠错码
TCP(传输控制协议)
威纶通触摸屏如何隐藏系统设置箭头图标及通过参数进入系统设置?
SQL实现将多行记录合并成一行
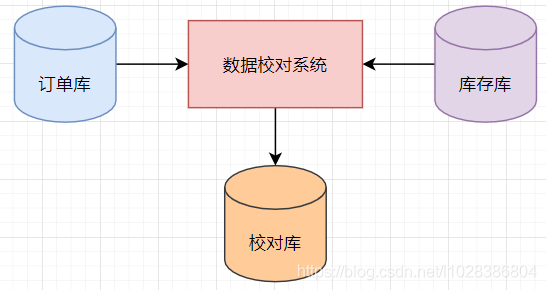
看我如何用多线程,帮助运营小姐姐解决数据校对系统变慢!
Go-4-在vim中无法跳转到源代码
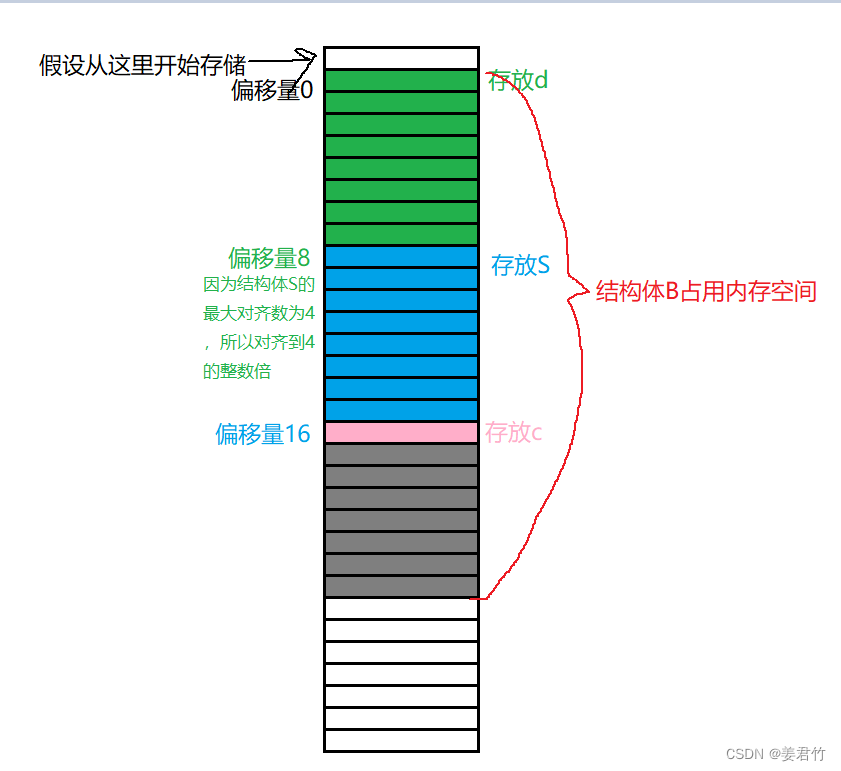
2.7 - 文件管理 2.8 - 多级目录结构 2.9 - 位示图
阿里巴巴《MySQL成长手册》精简版
QT | VS2017 + Qt5.14.2 环境搭建
WWW'22 推荐系统论文之多任务与对比学习篇
浅析PM2实用入门指南
Qt | 鼠标事件和滚轮事件 QMouseEvent、QWheelEvent
SSRF(服务器端请求伪造)
SIGIR'22 推荐系统论文之POI篇
禅道16.5升级17.3
AI智能剪辑,仅需2秒一键提取精彩片段
看我如何用多线程,帮助运营小姐姐解决数据校对系统变慢!
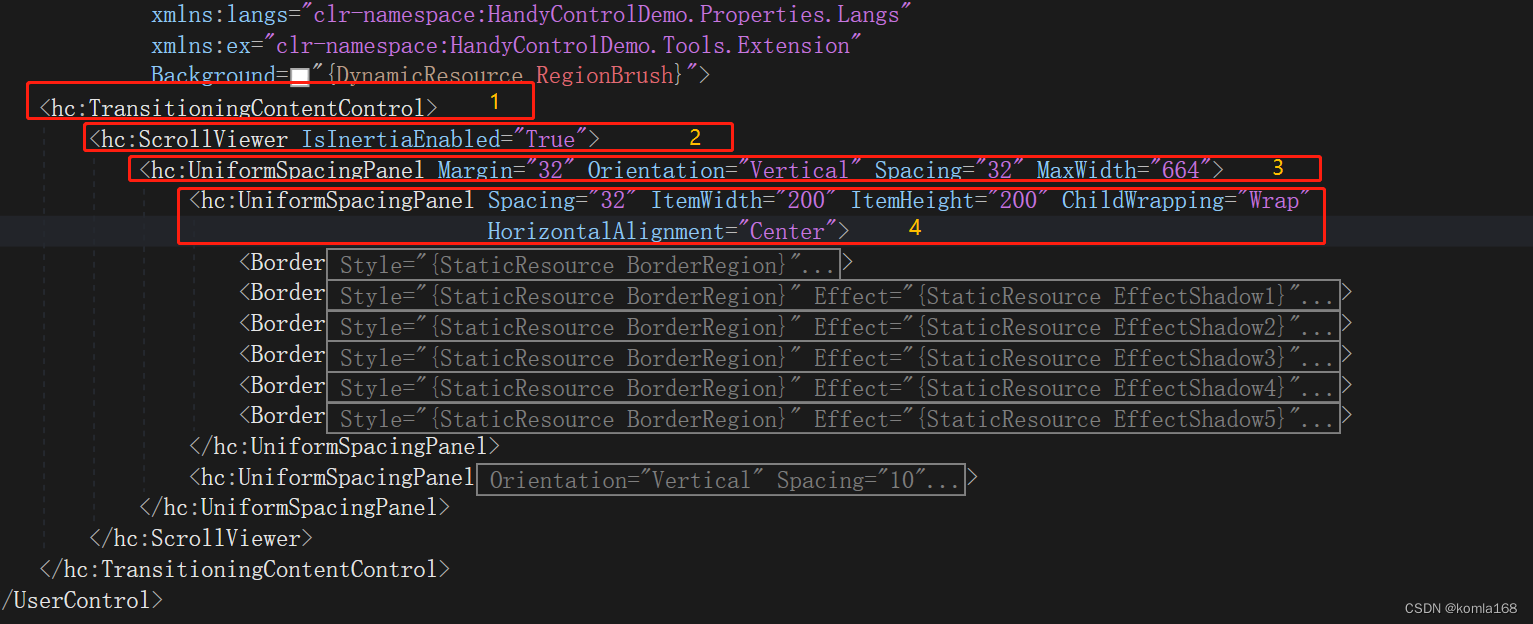
开篇-开启全新的.NET现代应用开发体验