当前位置:网站首页>LeetCode 1774. 最接近目标价格的甜点成本 每日一题
LeetCode 1774. 最接近目标价格的甜点成本 每日一题
2022-07-07 15:32:00 【@小红花】
问题描述
你打算做甜点,现在需要购买配料。目前共有 n 种冰激凌基料和 m 种配料可供选购。而制作甜点需要遵循以下几条规则:
必须选择 一种 冰激凌基料。
可以添加 一种或多种 配料,也可以不添加任何配料。
每种类型的配料 最多两份 。
给你以下三个输入:baseCosts ,一个长度为 n 的整数数组,其中每个 baseCosts[i] 表示第 i 种冰激凌基料的价格。
toppingCosts,一个长度为 m 的整数数组,其中每个 toppingCosts[i] 表示 一份 第 i 种冰激凌配料的价格。
target ,一个整数,表示你制作甜点的目标价格。
你希望自己做的甜点总成本尽可能接近目标价格 target 。返回最接近 target 的甜点成本。如果有多种方案,返回 成本相对较低 的一种。
示例 1:
输入:baseCosts = [1,7], toppingCosts = [3,4], target = 10
输出:10
解释:考虑下面的方案组合(所有下标均从 0 开始):
- 选择 1 号基料:成本 7
- 选择 1 份 0 号配料:成本 1 x 3 = 3
- 选择 0 份 1 号配料:成本 0 x 4 = 0
总成本:7 + 3 + 0 = 10 。
示例 2:输入:baseCosts = [2,3], toppingCosts = [4,5,100], target = 18
输出:17
解释:考虑下面的方案组合(所有下标均从 0 开始):
- 选择 1 号基料:成本 3
- 选择 1 份 0 号配料:成本 1 x 4 = 4
- 选择 2 份 1 号配料:成本 2 x 5 = 10
- 选择 0 份 2 号配料:成本 0 x 100 = 0
总成本:3 + 4 + 10 + 0 = 17 。不存在总成本为 18 的甜点制作方案。
示例 3:输入:baseCosts = [3,10], toppingCosts = [2,5], target = 9
输出:8
解释:可以制作总成本为 8 和 10 的甜点。返回 8 ,因为这是成本更低的方案。
示例 4:输入:baseCosts = [10], toppingCosts = [1], target = 1
输出:10
解释:注意,你可以选择不添加任何配料,但你必须选择一种基料。
提示:
n == baseCosts.length
m == toppingCosts.length
1 <= n, m <= 10
1 <= baseCosts[i], toppingCosts[i] <= 104
1 <= target <= 104来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/closest-dessert-cost
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
Java
class Solution {
int ans = Integer.MAX_VALUE;
public int closestCost(int[] baseCosts, int[] toppingCosts, int target) {
int n = baseCosts.length;
for(int i = 0;i < n;i++){
dfs(toppingCosts,0,baseCosts[i],target);
}
return ans;
}
public void dfs(int[] toppingCosts,int index,int sum,int target){
if(Math.abs(sum - target) < Math.abs(ans - target)) ans = sum;
else if(Math.abs(sum - target) == Math.abs(ans - target)) ans = ans < target ? ans : sum;
//更新结果后在判断
if(index == toppingCosts.length || sum >= target) return;
//加配料
for(int i = 0;i < 3;i++){
dfs(toppingCosts,index + 1,sum + toppingCosts[index] * i,target);
}
}
}边栏推荐
- LeetCode-SQL第一天
- null == undefined
- 【Vulnhub靶场】THALES:1
- 谈谈 SAP 系统的权限管控和事务记录功能的实现
- Record the migration process of a project
- 在哪个期货公司开期货户最安全?
- Binary search tree (basic operation)
- [PHP] PHP interface inheritance and interface multi inheritance principle and implementation method
- Master this set of refined Android advanced interview questions analysis, oppoandroid interview questions
- Build an all in one application development platform, light flow, and establish a code free industry benchmark
猜你喜欢

HAVE FUN | “飞船计划”活动最新进展
Master this set of refined Android advanced interview questions analysis, oppoandroid interview questions
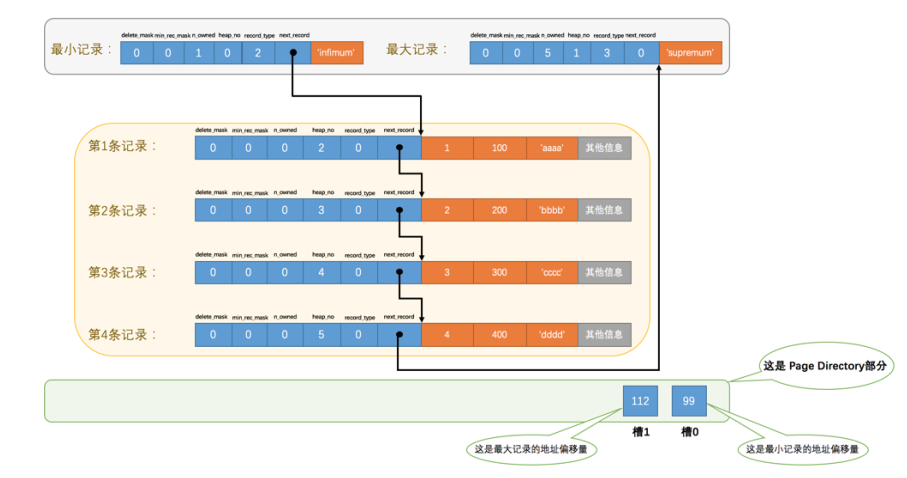
【MySql进阶】索引详解(一):索引数据页结构
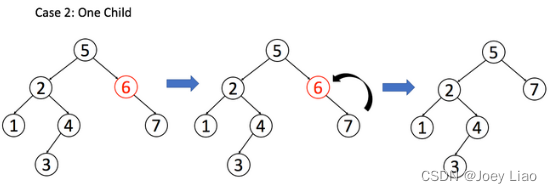
Binary search tree (basic operation)
记一次项目的迁移过程
Statistical learning method -- perceptron

华东师大团队提出,具有DNA调控电路的卷积神经网络的系统分子实现
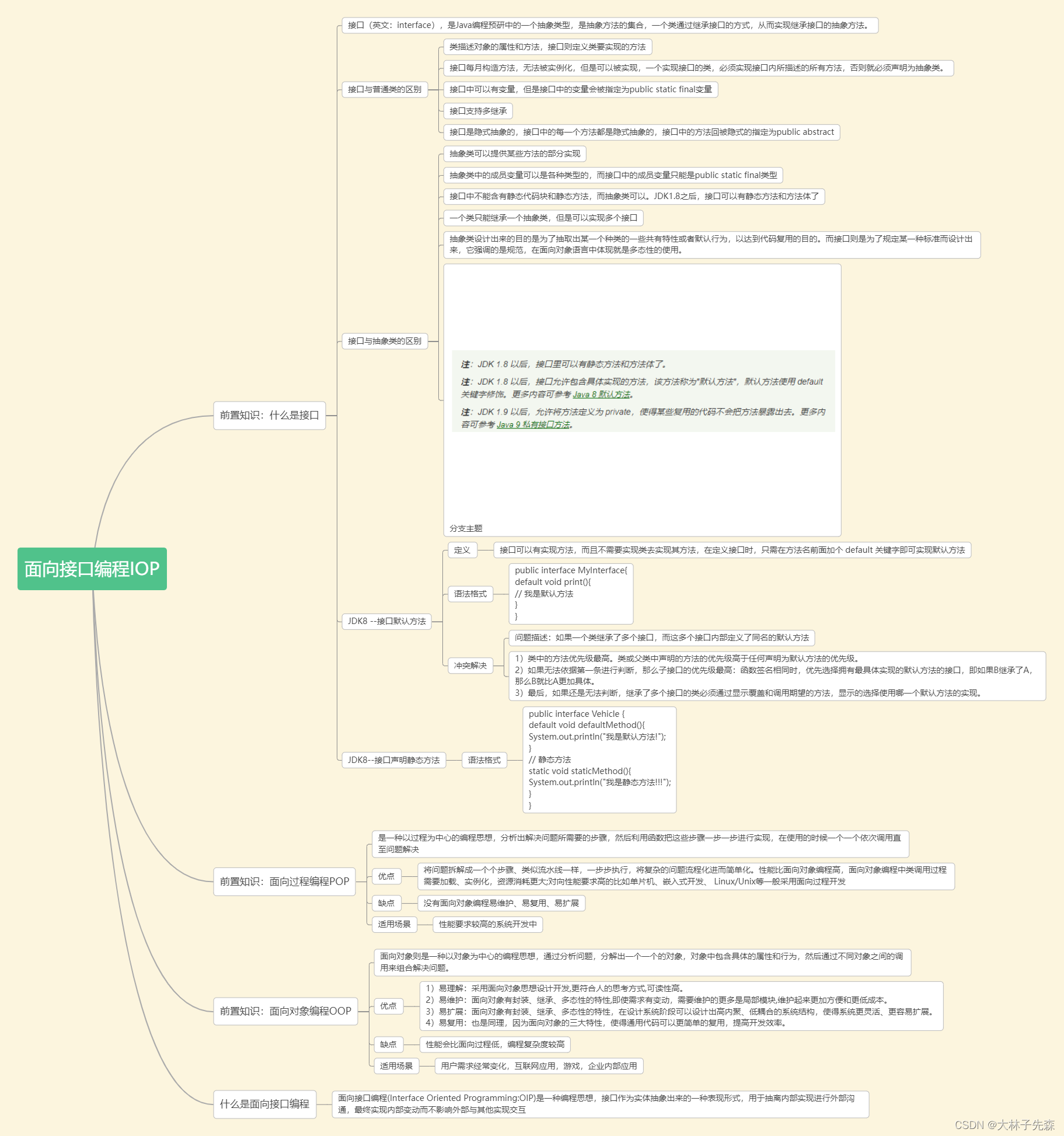
Interface oriented programming
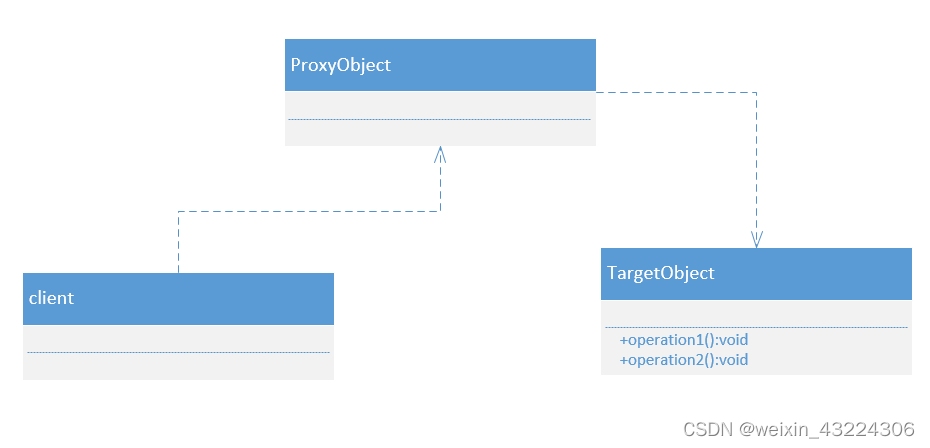
【DesignMode】代理模式(proxy pattern)
Advanced C language -- function pointer
随机推荐
Laravel5.1 Routing - routing packets
Asyncio concept and usage
How does laravel run composer dump autoload without emptying the classmap mapping relationship?
[PHP] PHP interface inheritance and interface multi inheritance principle and implementation method
Imitate the choice of enterprise wechat conference room
模块六
Personal notes of graphics (4)
Detailed explanation of several ideas for implementing timed tasks in PHP
打造All-in-One应用开发平台,轻流树立无代码行业标杆
The team of East China Normal University proposed the systematic molecular implementation of convolutional neural network with DNA regulation circuit
偶然升职的内心独白
ATM system
字节跳动高工面试,轻松入门flutter
Have fun | latest progress of "spacecraft program" activities
JS 模块化
laravel post提交数据时显示异常
null == undefined
laravel怎么获取到public路径
LocalStorage和SessionStorage
【医学分割】attention-unet