Leetcode 96. Différents arbres de recherche binaires

96. Différents arbres de recherche binaires

Pour vous donner un entier n ,Je vous en prie. n Les noeuds sont composés et les valeurs des noeuds sont de 1 À n Différents Arbre de recherche binaire Combien de？Renvoie le nombre d'arbres de recherche binaires qui répondent à l'intention du sujet.
Exemple 1：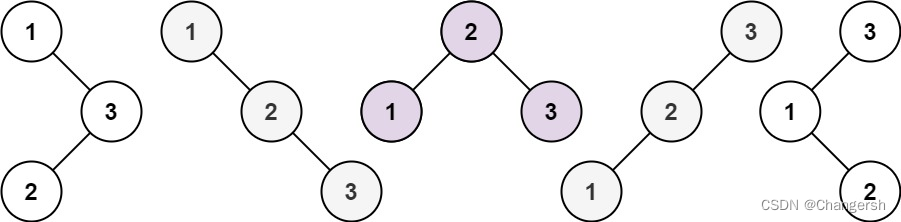

Entrée：n = 3
Produits：5

Exemple 2：

Entrée：n = 1
Produits：1

Conseils：

1 <= n <= 19

Idées

On peut mettren = 1 2 3 Ces trois situations sont énumérées,Et puis nous pouvons découvrir：
n = 1Heure,Il n'y a qu'un seul noeud,La valeur est:1,Il ne peut former qu'un arbre de recherche binaire.
n = 2Heure,1 2 C'est bon.1 Pour les noeuds,C'est possible.2Pour le noeud racine,Donc il y a deux situations.
n = 3Heure,C'est le cas de l'image ci - dessus,Cinq situations au total,Peut être divisé en trois grandes catégories：

1. 1Pour le noeud racine：Le reste est plus que1Grand,Donc le Sous - arbre gauche a 1 - 1 = 0Noeuds,Le Sous - arbre droit a3 - 1 = 2Noeuds,Donc la situation est redevenue deux noeuds dans le Sous - arbre droit,Zéro noeud dans le Sous - arbre gauche.Donc le nombre de fois = Sous - arbre gauche0Nombre de types de noeuds * Sous - arbre droit2Nombre de types de noeuds
2. 2Pour le noeud racine：Sous - arbre gauche 2 - 1 = 1Noeuds,Sous - arbre droit 3 - 2 = 1Noeuds,Donc le nombre de fois = Un noeud dans le Sous - arbre gauche * Un noeud dans le Sous - arbre droit
3. 3Pour le noeud racine：Sous - arbre gauche 3 - 1 = 2Noeuds,Sous - arbre droit 3 - 3 = 0Noeuds,Donc le nombre de fois = Deux noeuds dans le Sous - arbre gauche * Un noeud dans le Sous - arbre droit

Et nous pouvons aussi savoir , Le nombre d'espèces correspondant au nombre de noeuds dans les sous - arbres de gauche et de droite est égal à dp[i]Valeur de.
Alors...dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2];
Pour la section i Noeuds, Il faut envisager 1 À i En tant que noeud racine,Il faut donc additionner
C'est tout. i Noeuds,Pour le noeud racine j ,En ce moment,Le Sous - arbre gauche a j - 1 Noeuds,Le Sous - arbre droit a i - j Noeuds

Code

class Solution {
    
public:
    int numTrees(int n) {
    
        int dp[n + 1];
        for (int i = 0; i <= n; i++) dp[i] = 0;
        dp[0] = 1;

        for (int i = 1; i <= n; i++) {
    
            for (int j = 1; j <= i; j++) {
    
                dp[i] += dp[i - j] * dp[j - 1];
            }
        }

        return dp[n];
    }
};
/* //Pour la sectioniNoeuds,Il faut y réfléchir.1Comme noeud racine jusqu'àiEn tant que noeud racine,Il faut donc additionner //TotaliNoeuds,Pour le noeud racinejHeure,Le nombre de noeuds dans le Sous - arbre gauche estj-1,Le nombre de noeuds dans le Sous - arbre droit esti-j */

/* Élément1Nombre d'arbres de recherche pour les noeuds d'en - tête = Le Sous - arbre droit a2Nombre d'arbres de recherche pour les éléments * Le Sous - arbre gauche a0Nombre d'arbres de recherche pour les éléments Élément2Nombre d'arbres de recherche pour les noeuds d'en - tête = Le Sous - arbre droit a1Nombre d'arbres de recherche pour les éléments * Le Sous - arbre gauche a1Nombre d'arbres de recherche pour les éléments Élément3Nombre d'arbres de recherche pour les noeuds d'en - tête = Le Sous - arbre droit a0Nombre d'arbres de recherche pour les éléments * Le Sous - arbre gauche a2Nombre d'arbres de recherche pour les éléments Oui.2 Le nombre d'arbres de recherche pour les éléments est dp[2]. Oui.1 Le nombre d'arbres de recherche pour les éléments est dp[1]. Oui.0 Le nombre d'arbres de recherche pour les éléments est dp[0]. Alors...dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2] */