当前位置:网站首页>Wuenda machine learning course - week 7
Wuenda machine learning course - week 7
2022-06-11 10:14:00 【J___ code】
1. Support vector machine SVM
1.1 Optimization objectives
In logical regression , The loss function for a sample is as follows :
− y ( i ) l o g ( h θ ( x ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) = − y ( i ) l o g ( 1 1 + e − θ T ⋅ x ) + ( 1 − y ( i ) ) l o g ( 1 − 1 1 + e − θ T ⋅ x ) -y^{(i)}log(h_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)})=-y^{(i)}log(\frac{1}{1+e^{-\theta^T·x}})+(1-y^{(i)})log(1-\frac{1}{1+e^{-\theta^T·x}}) −y(i)log(hθ(x(i))+(1−y(i))log(1−hθ(x(i))=−y(i)log(1+e−θT⋅x1)+(1−y(i))log(1−1+e−θT⋅x1)
Suppose z = θ T ⋅ x z=\theta^T·x z=θT⋅x Abscissa , The value of the above loss function is the ordinate , When y y y Different images can be drawn with different values :
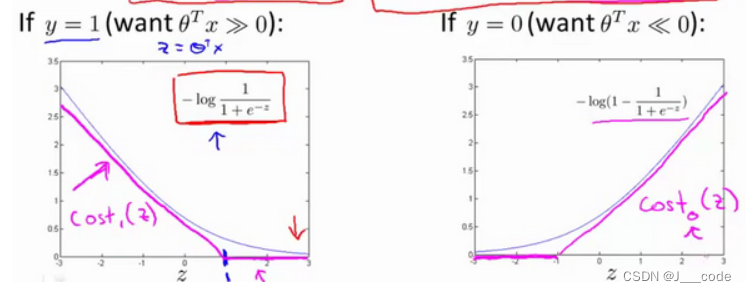
The blue curve in the above figure is the original image , The purplish red line is similar to the curve . If the new cost function is used to express the purple red line , It can be expressed as : min θ C ∑ i = 1 m [ y ( i ) cost 1 ( θ T x ( i ) ) + ( 1 − y ( i ) ) cost 0 ( θ T x ( i ) ) ] + 1 2 ∑ i = 1 n θ j 2 \min\limits_{\theta} C \sum_{i=1}^{m}\left[y^{(i)} \operatorname{cost}_{1}\left(\theta^{T} x^{(i)}\right)+\left(1-y^{(i)}\right) \operatorname{cost}_{0}\left(\theta^{T} x^{(i)}\right)\right]+\frac{1}{2} \sum_{i=1}^{n} \theta_{j}^{2} θminC∑i=1m[y(i)cost1(θTx(i))+(1−y(i))cost0(θTx(i))]+21∑i=1nθj2
The converted cost function is the cost function of support vector machine . among c o s t 1 ( θ T x ( i ) ) = − l o g h θ ( x ( i ) ) , c o s t 0 ( θ T x ( i ) ) = − l o g ( 1 − h θ ( x ( i ) ) ) cost_1(\theta^Tx^{(i)})=-logh_{\theta}(x^{(i)}),cost_0(\theta^Tx^{(i)})=-log(1-h_{\theta}(x^{(i)})) cost1(θTx(i))=−loghθ(x(i)),cost0(θTx(i))=−log(1−hθ(x(i))), Respectively represent the purple red lines in the two subgraphs , And in the above formula, the constants in the front and back parts 1 m \frac{1}{m} m1 And in the regularization term λ \lambda λ Delete , Change to... In Item 1 C C C, This is a SVM Common expressions , The actual meaning has not changed : The original formula can be understood as A + λ B A+\lambda B A+λB, If λ \lambda λ A higher value indicates that B B B The weight of the cost function is large ; Now change to C A + B CA+B CA+B, When C C C The value of is small , Disguised increase B B B The weight in the cost function , When C = 1 λ C=\frac{1}{\lambda} C=λ1 when , The two formulas will reach the same value when the gradient is updated
1.2 The intuitive understanding of the big boundary
The picture below is SVM The image of the cost function . When y = 1 y=1 y=1 when ( Corresponding to left subgraph ), In order to minimize the loss value z = θ T x ≥ 1 z=\theta^Tx \ge 1 z=θTx≥1; When y = 0 y=0 y=0 when ( Corresponding to right subgraph ), In order to minimize the loss value z = θ T x ≤ − 1 z=\theta^Tx \le -1 z=θTx≤−1. But in logistic regression, when y = 1 y=1 y=1 when , Only required θ T x ≥ 0 \theta^Tx \ge 0 θTx≥0 The sample can be correctly classified as a positive sample ; When y = 0 y=0 y=0 when , Only required θ T x < 0 \theta^Tx \lt 0 θTx<0 The sample can be correctly classified as a negative sample :

From the above analysis, we can see that SVM It's more demanding , Need one Safe spacing
When put C C C When the value is set to a large value , At this point, it is necessary to find out that the first item is 0 Parameters of θ \theta θ. Suppose that the first item is chosen to be 0 Parameters of θ \theta θ, The constraints must be followed , When y = 1 y=1 y=1 when , θ T x ≥ 1 \theta^Tx \ge 1 θTx≥1 And when y = 0 y=0 y=0 when , θ T x ≤ − 1 \theta^Tx \le -1 θTx≤−1:

Why? SVM It is called a large spacing classifier ? For the dataset in the figure below , You can use multiple lines to separate positive and negative samples , See the purple red and green straight lines in the picture . Compared with these two lines, the black line visually separates the two types of samples better , Because there is a greater shortest distance between the black line and the sample ( There are two distance values from two types of samples , The smaller of these values ), signify SVM Robust , This distance is called SVM The distance between :

When will C C C When it is set very large , Outliers can seriously affect decision boundaries . In the following illustration , When C C C large , The black line is the Red Cross not added to the lower left corner ( Outliers ) The resulting decision boundary . After adding outliers , In order to separate the samples with maximum spacing , The decision boundary changes from a black line to a purplish red line , It's obviously not very good ( It can be understood as over fitting ). So when C C C When the set value is not very large , The influence of outliers can be ignored , Get a better decision boundary like the black line :

1.3 The mathematics behind big boundary classification
First review the intuitive understanding of vector inner product , For two vectors u = [ u 1 , u 2 ] T , v = [ v 1 , v 2 ] T u=[u_1,u_2]^T,v=[v1,v2]^T u=[u1,u2]T,v=[v1,v2]T, p p p by v v v stay u u u The projection on the ( p p p There are also positive and negative values , But not a vector ), be u T v = p ⋅ ∣ ∣ u ∣ ∣ = u 1 v 1 + u 2 v 2 u^Tv=p·||u||=u_1v_1+u_2v_2 uTv=p⋅∣∣u∣∣=u1v1+u2v2:

Now let's understand through the inner product property SVM The objective function of :
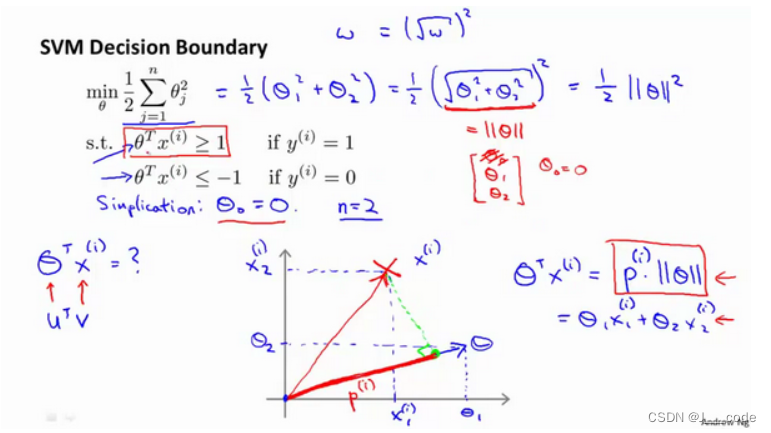
Let's start with θ 0 = 0 \theta_0=0 θ0=0, And set the characteristic number to n = 2 n=2 n=2, So the objective function is converted to :
min θ 1 2 ∑ j = 1 n θ j 2 = 1 2 ( θ 1 2 + θ 2 2 ) = 1 2 ( θ 1 2 + θ 2 2 ) 2 = 1 2 ∣ ∣ θ ∣ ∣ 2 \min\limits_\theta\frac{1}{2}\sum_{j=1}^n\theta_j^2=\frac{1}{2}(\theta_1^2+\theta_2^2)=\frac{1}{2}(\sqrt{\theta_1^2+\theta_2^2)}^2=\frac{1}{2}||\theta||^2 θmin21∑j=1nθj2=21(θ12+θ22)=21(θ12+θ22)2=21∣∣θ∣∣2
Through the previous intuitive introduction to inner product , constraint condition θ T x ( i ) = p ( i ) ∣ ∣ θ ∣ ∣ \theta^Tx^{(i)}=p^{(i)}||\theta|| θTx(i)=p(i)∣∣θ∣∣, p ( i ) p^{(i)} p(i) Express x ( i ) x^{(i)} x(i) stay θ \theta θ The projection on the . So the objective function is as follows :

Two types of samples in the left subgraph below , Suppose the green line is taken as the decision boundary ( namely θ T x = 0 \theta^Tx=0 θTx=0, The reason why the green line goes through the origin here is because θ 0 = 0 \theta_0=0 θ0=0), Then the blue vector θ \theta θ Orthogonal to the green line , So a decision boundary corresponds to a parameter θ \theta θ vector . Suppose the Red Cross is a positive sample , The blue circle is a negative sample , Then the positive sample in the figure x ( 1 ) x^{(1)} x(1) And negative samples x ( 2 ) x^{(2)} x(2) stay θ \theta θ The length of the projection on is very short , To meet the p ( i ) ∣ ∣ θ ∣ ∣ ≥ 1 p^{(i)}||\theta|| \ge 1 p(i)∣∣θ∣∣≥1 and p ( i ) ∣ ∣ θ ∣ ∣ ≤ − 1 p^{(i)}||\theta|| \le -1 p(i)∣∣θ∣∣≤−1 You need to ∣ ∣ θ ∣ ∣ ||\theta|| ∣∣θ∣∣ The value of is very large , But the objective function is to ∣ ∣ θ ∣ ∣ ||\theta|| ∣∣θ∣∣ The value of is as small as possible , therefore θ \theta θ The direction is not good ( That is, the choice of decision boundary is not good ).
SVM The decision boundary in the right subgraph below will be selected according to the objective function , Because the boundary makes ∣ ∣ θ ∣ ∣ ||\theta|| ∣∣θ∣∣ To become smaller :

1.4 Kernel function Ⅰ
In order to obtain the decision boundary in the figure below , The model could be h ( θ ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 x 2 + . . . h(\theta)=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1x_2+... h(θ)=θ0+θ1x1+θ2x2+θ3x1x2+... In the form of , Now suppose f 1 = x 1 , f 2 = x 2 , f 3 = x 1 x 2 , . . . f_1=x_1,f_2=x_2,f_3=x_1x_2,... f1=x1,f2=x2,f3=x1x2,..., be h ( θ ) = θ 0 + θ 1 f 1 + θ 2 f 2 + . . . + θ n f n h(\theta)=\theta_0+\theta_1f_1+\theta_2f_2+...+\theta_nf_n h(θ)=θ0+θ1f1+θ2f2+...+θnfn. In addition to combining the original features , Is there a better way to construct f 1 , f 2 , . . . f_1,f_2,... f1,f2,...? This requires a kernel function
Suppose a sample is given x x x, utilize x x x And pre selected tags l ( 1 ) 、 l ( 2 ) 、 l ( 3 ) l^{(1)}、l^{(2)}、l^{(3)} l(1)、l(2)、l(3) The degree of approximation as f 1 、 f 2 、 f 3 f_1、f_2、f_3 f1、f2、f3:

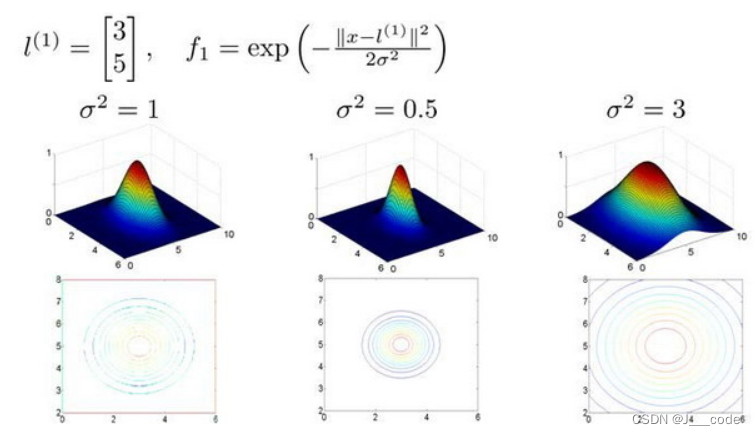
f 1 = similarity ( x , l ( 1 ) ) = e ( − ∥ x − l ( 1 ) ∥ 2 2 σ 2 ) f_{1}=\operatorname{similarity}\left(x, l^{(1)}\right)=e\left(-\frac{\left\|x-l^{(1)}\right\|^{2}}{2 \sigma^{2}}\right) f1=similarity(x,l(1))=e(−2σ2∥x−l(1)∥2)
f 2 = similarity ( x , l ( 2 ) ) = e ( − ∥ x − l ( 2 ) ∥ 2 2 σ 2 ) f_{2}=\operatorname{similarity}\left(x, l^{(2)}\right)=e\left(-\frac{\left\|x-l^{(2)}\right\|^{2}}{2 \sigma^{2}}\right) f2=similarity(x,l(2))=e(−2σ2∥x−l(2)∥2)
f 3 = similarity ( x , l ( 3 ) ) = e ( − ∥ x − l ( 3 ) ∥ 2 2 σ 2 ) f_{3}=\operatorname{similarity}\left(x, l^{(3)}\right)=e\left(-\frac{\left\|x-l^{(3)}\right\|^{2}}{2 \sigma^{2}}\right) f3=similarity(x,l(3))=e(−2σ2∥x−l(3)∥2)
among , similarity ( x , l ( i ) ) \operatorname{similarity}\left(x, l^{(i)}\right) similarity(x,l(i)) It's a kernel function ( This function is a Gaussian kernel function ), Usually used k ( x , l ( i ) ) k(x,l^{(i)}) k(x,l(i)) Express . When x x x Marking and marking l ( i ) l^{(i)} l(i) The closer we get to , Characteristics f i f_i fi Approximate to e − 0 = 1 e^{-0}=1 e−0=1; When x x x Marking and marking l ( i ) l^{(i)} l(i) The farther away you are , Characteristics f i f_i fi Approximate to e − b i g n u m = 0 e^{-bignum}=0 e−bignum=0. It can be understood intuitively from the following figure , When l ( 1 ) = [ 3 , 5 ] T l^{(1)}=[3,5]^T l(1)=[3,5]T when , If x = [ 3 , 5 ] T x=[3,5]^T x=[3,5]T, be z z z Axis Max ( z z z Axis representation f 1 f_1 f1 Value , x x x and y y y The axes are represented separately x 1 x_1 x1 and x 2 x_2 x2). in addition σ \sigma σ The value of will control f 1 f_1 f1 The value of the x x x The rate of change :
So how does the kernel function determine the decision boundary ? Suppose that h θ ( x ) = θ 0 + θ 1 f 1 + θ 2 f 2 + θ 3 f 3 h_\theta(x)=\theta_0+\theta_1f_1+\theta_2f_2+\theta_3f_3 hθ(x)=θ0+θ1f1+θ2f2+θ3f3, At this point, the parameters are known , Respectively θ 0 = 0.5 , θ 1 = θ 2 = 1 , θ 3 = 0 \theta_0=0.5,\theta_1=\theta_2=1,\theta_3=0 θ0=0.5,θ1=θ2=1,θ3=0. For the purplish red sample points in the figure below , It can be seen that it is far from l ( 1 ) l^{(1)} l(1) Closer , leave l ( 2 ) l^{(2)} l(2) and l ( 3 ) l^{(3)} l(3) Far away , therefore f 1 ≈ 1 , f 2 ≈ 0 , f 3 ≈ 0 f_1 \approx 1,f_2 \approx 0,f_3 \approx 0 f1≈1,f2≈0,f3≈0, therefore h θ ( x ) > 0 h_\theta(x)>0 hθ(x)>0, That is, it is predicted that the sample point is a positive sample point . Similarly, green sample points are predicted as positive sample points , Blue and blue sample points are negative sample points , Finally, the red decision boundary . It can be seen that the characteristic value of the sample is not used in the above calculation x 1 、 x 2 、 x 3 x_1、x_2、x_3 x1、x2、x3, Instead, new features calculated using kernel functions f 1 、 f 2 、 f 3 f_1、f_2、f_3 f1、f2、f3:

1.5 Kernel function Ⅱ
stay 1.4 The concept and function of kernel function are introduced in this section , But I still don't know how to select tags l ( i ) l^{(i)} l(i). The number of tags is usually selected according to the number of training sets , Suppose there is m m m Samples , Then choose m m m A sign , The new feature obtained in this way is based on the distance between a single sample point and all other sample points . Suppose each sample point is used as a marker , The new feature can be expressed as :

therefore SVM The objective function of is converted to min θ C ∑ i = 1 m [ y ( i ) cost 1 ( θ T f ( i ) ) + ( 1 − y ( i ) ) cost 0 ( θ T f ( i ) ) ] + 1 2 ∑ i = 1 n = m θ j 2 \min\limits_{\theta} C \sum_{i=1}^{m}\left[y^{(i)} \operatorname{cost}_{1}\left(\theta^{T} f^{(i)}\right)+\left(1-y^{(i)}\right) \operatorname{cost}_{0}\left(\theta^{T} f^{(i)}\right)\right]+\frac{1}{2} \sum_{i=1}^{n=m} \theta_{j}^{2} θminC∑i=1m[y(i)cost1(θTf(i))+(1−y(i))cost0(θTf(i))]+21∑i=1n=mθj2, And calculating ∑ i = 1 n = m θ j 2 = θ T θ \sum_{i=1}^{n=m} \theta_{j}^{2}=\theta^T\theta ∑i=1n=mθj2=θTθ Will use θ T M θ \theta^T M \theta θTMθ To replace , Because of the simplified calculation , among M M M Varies with the kernel function
Be careful : When SVM When kernel functions are not used , It is called a linear kernel function , That is, the objective function or θ T x \theta^Tx θTx
Let's take a look C = 1 λ C=\frac{1}{\lambda} C=λ1 and σ \sigma σ Yes SVM Influence :
- When C C C large , amount to λ \lambda λ smaller , May cause over fitting , High variance
- When C C C More hours , amount to λ \lambda λ more , May lead to under fitting , High deviation
- When σ \sigma σ large , features f i f_i fi The change of is smooth , May lead to low variance , High deviation
- When σ \sigma σ More hours , features f i f_i fi The change of is more drastic , May cause low deviation , High variance
1.6 SVM Use
To use SVM, The following things must be done :
- Choose the right one C C C value
- Select kernel function ( It is also possible not to use kernel functions ), Kernel function except Gaussian kernel function , There are also polynomial kernel functions , But the goal is to build new features based on the distance between the sample and the marker
- Choose the right one σ \sigma σ value
about SVM There are universal rules for the use of , m m m Sample size , n n n Characteristic number :
If n n n Compare with m m m It's much bigger , That is, the amount of data in the training set is not enough to support the training of a complex nonlinear model , The logistic regression model or the one without kernel function is used SVM
If n n n smaller , m m m Moderate size , Then the Gaussian kernel function is used SVM
If n n n smaller , m m m more , Then use SVM Will be very slow , More features need to be created , Then we use logistic regression or the function without kernel SVM
Neural network in the above three cases may have better performance , But training neural networks can be very slow , The main reason for choosing support vector machine is that its cost function is convex function , There is no local minimum
2. Reference resources
https://www.bilibili.com/video/BV164411b7dx?p=70-75
http://www.ai-start.com/ml2014/html/week7.html
边栏推荐
- Habitable planet
- Tree topology networking structure of ZigBee module communication protocol
- 不卷了!入职字节跳动一周就果断跑了。
- After four years of outsourcing, it was abandoned
- 有哪些ABAP关键字和语法,到了ABAP云环境上就没办法用了?
- Bcgcontrolbar Library Professional Edition, fully documented MFC extension class
- Function and function of wandfluh proportional valve
- DOtween使用方法
- Secret behind the chart | explanation of technical indicators: tangqi'an channel
- Picture rule page turning
猜你喜欢

After four years of outsourcing, it was abandoned

No more! The entry byte beat for a week and ran decisively.

What are the application fields of MAG gear pump? To sum up

科技云报道:Web3.0浪潮下的隐私计算

Q1 revenue exceeded expectations. Why did man Bang win headwind growth?

Q1营收超预期,满帮为何赢得逆风增长?

Ugui picture wall

What are the functions and functions of the EMG actuator

Correct opening method of RPC | understand go native net/rpc package
Detailed explanation of Lora module wireless transceiver communication technology
随机推荐
MySQL permission management and backup
General idea of interface tuning
【Objective-C】‘NSAutoreleasePool‘ is unavailable: not available in automatic reference counting mode
Servlet 的初次部署
EMG执行器的作用和功能有哪些
Mysql比较
Technology cloud report: privacy computing under the wave of Web3.0
面试复习手写题--函数截流与抖动
对于力士乐电磁换向阀的功能与作用,你知道多少
MySQL basic learning notes 03
[Bert]: Calculation of last ave state when training tasks with similar Bert semantics
【bert】:在训练bert 语义相似的任务时,last ave state 的计算
帝国CMS仿《手艺活》DIY手工制作网源码/92kaifa仿手艺活自适应手机版模板
BeanFactoryPostProcessor 与BeanPostProcessor的区别
鼠标点击坐标转换生成
Troubleshooting the error ora-12545 reported by scanip in Oracle RAC
UGUI
Differences between beanfactorypostprocessor and beanpostprocessor
Chemical composition of q355hr steel plate
puppeteer入门之 Puppeteer 类