Leetcode detailed explanation of stack type

When I brush the question, I come across a suffix expression question , Then I feel that this problem is a classic stack application type problem , Just by this question , Let's talk about the usage of stack , Solved this problem by the way .

as everyone knows , Stack is a first in and last out data structure , Use this feature , It is very common in program design , Such as ： Parentheses matching 、 Expression evaluation 、 The application in recursion is inseparable from the data structure of stack .

Let me give you a brief introduction one by one .（PS： I will not repeat the data structure of the stack here , You can learn about ）

1. The application of stack in bracket matching

Suppose two parentheses are allowed in an expression ：｜ straight ｜ Brackets and brackets , Its nesting In any order namely （［］（）） or ［（［］[ ]）］ And so on are in the correct format ,［（］） or （［（）） or （（）］ Are in incorrect format .

We consider the following sequence of parentheses ：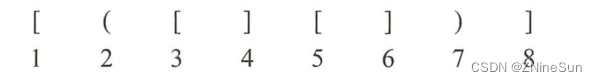

Let's analyze it briefly ：

• The computer receives the 1 A bracket “ ［ ” after , Look forward to matching the 8 A bracket “ ］” appear .
• Got the 2 A bracket “（”, At this time 1 A bracket “［” Put it aside for the time being , And urgently look forward to matching the first 7 A bracket “）” appear .
• Got the 3 A bracket “ ［ ”, At this time 2 Gekuo Number “（” Put it aside for the time being , And urgently look forward to matching the first 4 A bracket “］” appear . The first 3 A bracket Your expectations are met , After digestion , The first 2 A bracket The expectation matching becomes The most urgent task at present .
• And so on , It can be seen that the process and the idea of stack 、 Coincide .

We will follow the above process , The following design ideas can be given ：

• Initialize a stack stack, Start scanning the parenthesis strings in turn string, When you meet [ ’ 、 ( ’ When you open a bracket, push it onto the stack .
• When a right parenthesis is encountered, it will check whether the element at the top of the stack is the left parenthesis corresponding to this right parenthesis , If it corresponds to , Then the corresponding left bracket is pushed out of the stack , If it doesn't correspond to , The expression is wrong , return false.
• Only the left parenthesis is pushed into the stack during the process , When the expression is correct , Finally, the stack will turn the left bracket out of the stack again and again and become an empty stack .
• After scanning all characters , Check whether the stack is empty , if , return true, Otherwise return to false.

Title source ：20. Valid parenthesis
answer ：(PS:Java edition )

    public boolean isValid(String s) {
    
        Stack<Character> stack = new Stack<Character>();
        for (int i = 0; i < s.length(); i++) {
    
            char c = s.charAt(i);
            if (c == '(' || c == '[' || c == '{') {
    
                stack.push(c);
            } else {
    
                if (stack.isEmpty()) return false;
                char topChar = stack.pop();
                if (c == ')' && topChar != '(') return false;
                if (c == ']' && topChar != '[') return false;
                if (c == '}' && topChar != '{') return false;
            }
        }
        // Judge whether the stack is empty 
        if (stack.isEmpty()) return true;
        return false;
    }

2. The application of stack in expression evaluation

Expression evaluation is a programming language compilation in One of the most basic The problem of , Its implementation is a typical example of finding applications .

Infix expressions not only depend on the priority of operators , And you have to deal with parentheses . The operator of the suffix expression is after the operand , The priority of the operator has been considered in the suffix expression , There are no brackets , Only operands and operators .

Infix expression A+B*(C-D)-E/F The corresponding suffix expression is ABCD-*EF/-.

It involves a knowledge point , Infix is how our normal operation order becomes a suffix expression ？ If you are good at data structure, you can skip this section .

2.1 Infix expression converted to suffix expression

Let me just give an example .
Infix expression a+b - a* ( (c+d) /e- f) + g
This formula should be relatively representative , Let's see how to make it a suffix .

Let's first determine the priority of the good luck operator , namely ‘*,/’ > ‘±’>‘()’
about (), The left parenthesis indicates that the parentheses match successfully only when the right parenthesis is encountered , Go straight back to the stack , The left parenthesis encountered another character , Go straight to the stack .
Right bracket , When encountering other characters , Will keep other characters off the stack , Back to the left bracket , With the left parenthesis , No output .

The following steps are ： High priority , Go straight to the stack , If the priority is small or equal, it will be returned to the stack （PS: If the symbols are the same , Without the operating , Go straight to the stack ）, At the same time, put the priority on the stack .

meanwhile , If a value is encountered, it will be output directly
So let's see ：a+b - a* ( (c+d) /e- f) + g How is the suffix of this formula realized step by step

step	Scan item	Item type	action	Stack content	Output
1	a	The number	Direct output	empty	a
2	+	The operator	The stack is empty , There is no need to compare priorities , Into the stack	+	There is no output
3	b	The number	Direct output	+	b
4	-	The operator	+ and - Same priority , First, perform a stack withdrawal , The output +, In making - Into the stack	-	+
5	a	Operands	Direct output	-	a
6	*	The operator	* Than - High priority , Go straight to the stack	-*	There is no output
7	（	The operator	Go straight to the stack	-*（	There is no output
8	(	The operator	Go straight to the stack	-*（（	There is no output
9	c	Operands	Direct output	-*（（	c
10	+	The operator	+ priority >(, Direct stack	-*（（+	There is no output
11	d	Operands	Direct output	-*（（+	d
12	)	The operator	Let the elements at the top of the stack go back to the stack , Until I met ( until	-*（	+
13	/	The operator	Priority ratio ( high , Into the stack	-*(/	There is no output
14	e	Operands	Direct output	-*(/	e
15	-	The operator	- Than / Low priority ,/ Backstack ,- Into the stack	-*(-	/
16	f	Operands	Direct output	-*(-	f
17	)	The operator	Let the top element of the stack always output , At the same time with ( Back together	-*	-
18	+	The operator	Priority ratio * low ,* Back off the stack and output , and - Same priority ,- Back off the stack and output ,+ Into the stack	+	* -
19	g	Operands	Direct output	+	g
20	End of scan string , Let the elements in the stack go back to the stack in turn	-	Direct off stack output	Empty stack	+

Finally, connect the output elements in turn ：

ab+acd+e/f-*-g+

This expression is our suffix expression

2.2 The calculation of suffix expression

Finally, start the calculation , The most common method we use is to calculate the final result through the suffix expression , The calculation process is as follows ：

step	Scan item	Item type	action	Stack content
1	-	-	Empty stack	empty
2	a	Operands	Into the stack	a
2	b	Operands	Into the stack	a b
3	+	The operator	b,a Back off the stack in turn , The result of the calculation is b+a, result r1 Into the stack	r1
4	a	Operands	Into the stack	r1 a
5	c	Operands	Into the stack	r1 a c
6	d	Operands	Into the stack	r1 a c d
7	+	The operator	d,c Back off the stack in turn , The result of the calculation is d+c, result r2 Into the stack	r1 a r2
8	e	Operands	Into the stack	r1 a r2 e
9	/	The operator	e,r2 Back off the stack in turn , Calculation e/r2, result r3 Into the stack	r1 a r3
10	f	Operands	Go straight to the stack	r1 a r3 f
11	-	The operator	f,r3 Back off the stack in turn , Calculation f-r3, result r4 Into the stack	r1 a r4
12	*	The operator	r4 a Back off the stack in turn , Calculation a*r4, result r5 Into the stack	r1 r5
13	-	The operator	r5,r1 Back off the stack in turn , Calculation r5-r1, result r6 Into the stack	r6
14	g	Operands	Into the stack	r6 g
15	+	The operator	g r6 Back off the stack in turn , Calculation g+r6, result r7 Into the stack	r7

The final result is the last element in the stack .

    public int evalRPN(String[] tokens) {
    
        Stack<Integer> stack = new Stack<Integer>();
        int n = tokens.length;
        for (int i = 0; i < n; i++) {
    
            String token = tokens[i];
            if (isNumber(token)) {
    
                stack.push(Integer.parseInt(token));
            } else {
    
                int num2 = stack.pop();
                int num1 = stack.pop();
                switch (token) {
    
                    case "+":
                        stack.push(num1 + num2);
                        break;
                    case "-":
                        stack.push(num1 - num2);
                        break;
                    case "*":
                        stack.push(num1 * num2);
                        break;
                    case "/":
                        stack.push(num1 / num2);
                        break;
                    default:
                }
            }
        }
        return stack.pop();
    }

    public boolean isNumber(String token) {
    
        return !("+".equals(token) || "-".equals(token) || "*".equals(token) || "/".equals(token));
    }

Reference topic ： The finger of the sword Offer II 036. Postfix expression