509. 斐波那契数、爬楼梯所有路径、爬楼梯最小花费

509. 斐波那契数

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：
F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给定 n ，请计算 F(n) 。

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

输入：4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

给你个4,4是需要3和2,3需要2和1,2需要1和1

从1遍历到该数 用数组保存遍历的值

class Solution {
    
public:
    int fib(int n) {
    
     if(n<=1) return n;
     vector<int> temp(n+1);
     temp[0]=0;
     temp[1]=1;
     for(int i=2;i<=n;i++){
    
        temp[i]=temp[i-1]+temp[i-2];
     }
     return temp[n];
    }
};

不用维护从1到n整个数字，用两个数值保存

class Solution {
    
public:
    int fib(int n) {
    
     if(n<=1) return n;
     vector<int> temp(2);
     temp[0]=0;
     temp[1]=1;
     for(int i=2;i<=n;i++){
    
        temp[i%2]=temp[(i-1)%2]+temp[(i-2)%2];
     }
     return temp[n%2];
    }
};

递归的方式

终点是返回1和0

class Solution {
    
public:
    int fib(int n) {
    
     if(n<=1) return n;
     return fib(n-1)+fib(n-2);
    }
};

70. 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

确定递推式（动态规划）

1、确定dp数组以及下标的含义和递推式

dp[i]=dp[i-1]+dp[i-2];

表示爬到当前层有从下一层和下下层两者方法的加和
2、dp数组初始化

dp[1]=1;
dp[2]=2;

3、确定遍历的顺序
迭代的方式 用数组保存从前到后
递归的方式 从后往前，但是也是从前开始计算的

1、迭代的方式，用数组保存（动态规划）

class Solution {
    
public:
    int climbStairs(int n) {
    
        if(n<=2) return n;
        vector<int>dp(n+1);
        dp[1]=1;
        dp[2]=2;
        for(int i=3;i<=n;i++)
        {
    
            dp[i]=dp[i-1]+dp[i-2];

        }
        return dp[n];
    }
};

2、不用维护从1到n整个数字，用两个数值保存（动态规划）

class Solution {
    
public:
    int climbStairs(int n) {
    
        if(n<=2) return n;
        vector<int>dp(n+1);
        dp[0]=2;
        dp[1]=1;
        for(int i=3;i<=n;i++)
        {
    
            dp[i%2]=dp[(i-1)%2]+dp[(i-2)%2];

        }
        return dp[n%2];
    }
};

3、递归的方式（动态规划）

class Solution {
    
public:
    int climbStairs(int n) {
    
        if(n<=2) return n;
        return climbStairs(n-1)+ climbStairs(n-2);
    }
};

4、回溯法

下面这个代码结果是正确的，用我的电脑运行了快十五秒，但是用其他的代码只用了几秒。

class Solution {
    
public:
    int climbStairs(int n) {
    
        int count = 0;
        dfs(n, 0, count);
        return count;
    }
    int dfs(int n, int index, int& count) {
    
        if (n == index)count++;
        if (index > n) return -1;
        //当前状态可以选择爬一步，也可以选择爬两步
        //爬一步
        dfs(n, index + 1, count);
        //爬两步
        dfs(n, index + 2, count);
        return -1;
    }
};

5、对于递归和回溯出现超时的原因

递归法出现了大量重复计算，比如我爬上10层，如下图有两个分支，一个是直接8层，一个是从9层延续到8层，这样就会出现大量的重叠。如果递归树继续往下画，重叠就会更多，递归法计算了大量的重叠子问题而导致效率低下。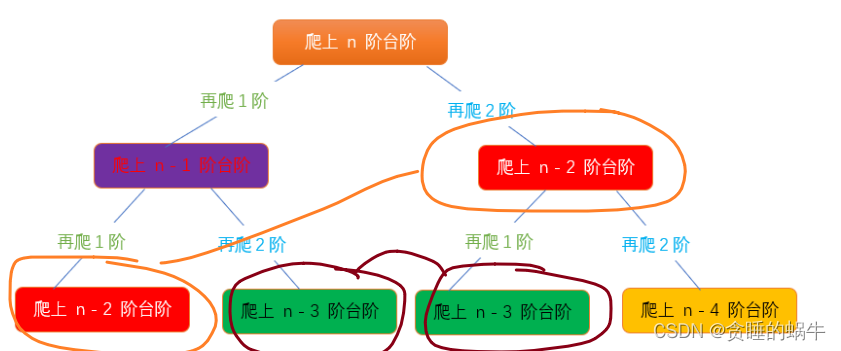

对于回溯法同样也是，此时的我是在楼梯中的一层，有很多分支会通过我，但是当第一个分支通过我已经计算了从我到达顶点的有多少种方法，但是其余的分支经过我竟然还进行了重复计算，这就造成了浪费。

解决方法：增加一个全局容器，存储信息
对于回溯而言。

class Solution {
    
public:
    vector<int>memo;
    int climbStairs(int n) {
    
        int count = 0;
        memo = vector<int>(n + 1, -1);
        dfs(n, 0, count);
        return count;
    }
    int dfs(int n, int index, int& count) {
    
        if (n == index) {
     count++; return -1; }
        if (index > n) return -1;
        if (memo[index] != -1) {
     count += memo[index]; return -1; }

        int temp = count;

        //当前状态可以选择爬一步，也可以选择爬两步
        //爬一步
        dfs(n, index + 1, count);
        //爬两步
        dfs(n, index + 2, count);
        memo[index] = count - temp;
        return -1;

    }
};

class Solution {
    
public:
    vector<int>memo;
    int climbStairs(int n) {
    
        memo = vector<int>(n + 1, -1);
       return  dfs(n);
    }
    int dfs(int n) {
    
        if (n <= 2) return n;
        if (memo[n] != -1) return memo[n];

        int count= dfs(n - 1)+ dfs(n - 2);
        memo[n] = count;
        return count;
    
    }
};

746. 使用最小花费爬楼梯

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

输入：cost = [1,100,1,1,1,100,1,1,100,1]
输出：6
解释：你将从下标为 0 的台阶开始。

• 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
• 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
• 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
• 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
• 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
• 支付 1 ，向上爬一个台阶，到达楼梯顶部。
  总花费为 6 。

确定递推式

1、dp数组以及下标的含义
dp[i]表示到达第i层的最小花费
2、确定递推公式
到达i层有两种方式，一种是dp[i-1],一种是dp[i-2]，那么选最小的

dp[i]=min{
    dp[i-1],dp[i-2]}+cost[i];

为什么是cost[i]，由于题目意思是上到i需要那些体力，因此就应该到哪就要花费到那的体力
3、dp数组初始化
dp[0] = cost[0];
dp[1] = cost[1];
4、确定遍历的顺序
从前到后遍历一遍就可以了

代码

class Solution {
    
public:
    int minCostClimbingStairs(vector<int>& cost) {
    
        vector<int>dp(cost.size());
        dp[0] = cost[0];
        dp[1] = cost[1];
        for (int i = 2; i <cost.size(); i++) {
    
          dp[i] = min(dp[i - 1],dp[i - 2] ) + cost[i];
        }
        return min(dp[cost.size() - 1], dp[cost.size() - 2]);
    }
};