[Brillouin phenomenon] Study on simultaneous measurement system of Brillouin temperature and strain distribution in optical fiber

1. Software version

matlab2013b

2. System Overview

        The research status of Brillouin distributed optical fiber sensing technology is summarized in detail ; The dependence of Brillouin frequency shift and intensity on fiber temperature and strain is studied theoretically and experimentally ; A distributed Brillouin optical fiber sensing system with heterodyne detection is designed, which can measure temperature and strain simultaneously , Light emission to it 、 Light reception 、 Data processing and other subsystems are analyzed in detail ; With electro-optic modulator （EOM） Based on the performance test , The system parameters are optimized , Realized  10 km  Optical fiber 、10 m  Measurement of optical time domain reflection waveform with spatial resolution ; The SNR of the designed system is deduced and calculated （SNR）、 Temperature and strain resolution 、 Dynamic range 、 Measurement time and other indicators ; Put forward the idea of  Golay  The idea of applying complementary sequences to Brillouin sensing systems , The simulation results show that , use  Golay  Complementary sequence driven  EOM  And correlation detection technology has greatly improved the signal-to-noise ratio and temperature and strain resolution of the system .

      Brillouin scattering is a scattering phenomenon that occurs when light propagates in inhomogeneous media , Its frequency and intensity change with respect to the incident light , The variation of Brillouin scattering relative to the frequency of incident light is called Brillouin frequency shift . Brillouin frequency shift and intensity are related to sound velocity in optical fiber materials , The sound velocity will be affected by the thermo optic and elasto optic properties of optical fiber materials , The thermo optic effect and elasto optic effect in optical fiber are related to the refractive index of optical fiber material 、 Young's modulus 、 Poisson's ratio is related to density , Therefore, the change of temperature and strain in optical fiber will cause the change of Brillouin frequency shift and intensity . In this chapter, the refractive index of optical fiber materials is analyzed theoretically 、 Young's modulus 、 Poisson's ratio and density versus fiber temperature and strain , The dependence of Brillouin frequency shift and intensity on temperature and strain is studied theoretically and experimentally .
        When the optical signal passes through the medium , Some of them will deviate from the original propagation direction and scatter into space . Scattered light at intensity 、 Direction 、 The polarization state and even the spectrum may be different from the incident light . The characteristics of light scattering and the composition of the medium 、 structure 、 There is a close relationship between the uniformity and the change of state . In a nutshell , The cause of light scattering can be regarded as the optical inhomogeneity or refractive index inhomogeneity of the medium , It makes the local area in the medium form the scattering center . There are many reasons for medium inhomogeneity , It can be divided into several scattering forms with different mechanisms . Brillouin scattering is caused by sound waves or acoustic subwaves . Raman scattering is caused by vibrational or optical acoustic wavelets inside molecules . The view of quantum theory shows that , Light scattering is composed of photons and microscopic particles （ atom 、 molecular 、 Electrons and phonons ） Caused by a collision , The result of the collision makes the incident photon scatter into a scattered photon with different energy or direction from the incident photon , Accordingly, the energy and momentum of micro particles change , And follow the law of conservation of energy and momentum .
 

3. Part of the source code

clc;
clear;
close all;
warning off;

% The relation between Brillouin frequency shift and temperature and strain is 
%v0     :  Incident light frequency 
%lmdap  :  Wavelength of incident light in vacuum 
%n(e,T) : Refractive index 
%E(e,T) : Young's modulus 
%k(e,T) : Poisson's ratio 
%p(e,T) : Core density 
%VB(e,T) = 2*v0*n(e,T) * sqrt( ((1-k(e,T))*(E(e,T)))/((1 + k(e,T))*(1-2*k(e,T))*(p(e,T))) )/lmdap;

To     = 20;% initial temperature 
T      = [20:1:40];% Temperature variation range 

lmdap  = 1550;% Wavelength of incident light in vacuum 
v0     = 9.853e8;% Incident light frequency 
% According to the requirements of the paper , Simulation considering the case of no strain 
% Define the variables 
% Core density 
p    = zeros(1,length(T));
beta = zeros(1,length(T));
% Refractive index 
n    = zeros(1,length(T));  
% Young's modulus 
E    = zeros(1,length(T));  
% Poisson's ratio 
k    = zeros(1,length(T));

ind  = 0;
for i = 1:length(T)
    % Core density 
%     beta    = (0.37 + 7.34*(T(i)-To)/10000)/1000000; 
%     p(i)    = M/(pi*ro*ro*lo*(1+beta)^3);%ro Is the fiber radius ,lo Is the fiber length 
    p(i)    = 2200.17 - 4.04*T(i)/1000;
    % Refractive index 
    n(i)    = 1.45 + 2.12*T(i)/100000;
    % Young's modulus 
    E(i)    = (7.25+1.35*T(i)/1000)*(10000000000);
    % Poisson's ratio 
    k(i)    = 0.17 + 4.515*T(i)/100000;
    % Brillouin frequency shift 
    VB(i) = 2*v0*n(i) * sqrt( ((1-k(i))*(E(i)))/((1 + k(i))*(1-2*k(i))*(p(i))) )/lmdap;
end
% The above is the Brillouin frequency shift obtained from the Brillouin frequency shift formula 

% The two methods are compared 
figure;
subplot(221):plot(T,p,'b-*') ;title(' Core density - Temperature curve '); 
subplot(222):plot(T,n,'b-*') ;title(' Refractive index - Temperature curve '); 
subplot(223):plot(T,E,'b-*') ;title(' Young's modulus - Temperature curve '); 
subplot(224):plot(T,k,'b-*') ;title(' Poisson's ratio - Temperature curve '); 
figure;
plot(T,VB,'b-*');title(' Brillouin frequency shift - Temperature curve '); 
% The above simulation verifies the linear relationship between Brillouin frequency shift and temperature 


 




% According to the formula and calculation, the following VB Value to plot Brillouin frequency shift — temperature , distance 3D chart 
% According to the formula and calculation, the following VB Value to plot Brillouin frequency shift — temperature , distance 3D chart 
% According to the formula and calculation, the following VB Value to plot Brillouin frequency shift — temperature , distance 3D chart 
% There will be , All parameters related to temperature change are calculated by formula 
%%%%%%%%%%%%%%%%%%%%%%%% The following parameters are set as adjustable parameters %%%%%%%%%%%%%%%%%%%%%%%%%%%%%
To        = 20;      % initial temperature 
dis       = 0:50:4000;% Define the distance 
T         = 20*ones(1,length(dis));% Temperature variation range 
if_change = 1;% Whether to set the mutation point 

if if_change == 1
    % Set the temperature better 
    s1 = 30;
    e1 = 40;
    s2 = 50;
    e2 = 60;
    T(s1:e1)= 30;
    T(s2:e2)= 40;
else
    T  =  T; 
end

% Set the 3D display area 
f = [10.8e9:1e6:11.2e9]/1e6;% Set the frequency range to be displayed , It can be set at will , In order to save computation, interpolation , Remove the frequency 1000000
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Core density 
p    = zeros(1,length(T));
beta = zeros(1,length(T));
% Refractive index 
n    = zeros(1,length(T));  
% Young's modulus 
E    = zeros(1,length(T));  
% Poisson's ratio 
k    = zeros(1,length(T));

ind  = 0;
for i = 1:length(T)
    % Core density 
%     beta    = (0.37 + 7.34*(T(i)-To)/10000)/1000000; 
%     p(i)    = M/(pi*ro*ro*lo*(1+beta)^3);%ro Is the fiber radius ,lo Is the fiber length 
    p(i)    = 2200.17 - 4.04*T(i)/1000;
    % Refractive index 
    n(i)    = 1.45 + 2.12*T(i)/100000;
    % Young's modulus 
    E(i)    = (7.25+1.35*T(i)/1000)*(10000000000);
    % Poisson's ratio 
    k(i)    = 0.17 + 4.515*T(i)/100000;
    % Brillouin frequency shift 
    VB2(i)  = 2*v0*n(i) * sqrt( ((1-k(i))*(E(i)))/((1 + k(i))*(1-2*k(i))*(p(i))) )/lmdap;
end
% The Brillouin frequency shift with different transmission distance is obtained 
 

% Set the 3D display area 
f = [10.8e3:1:11.2e3];% Set the frequency range to be displayed , It can be set at will , In order to save computation, interpolation , Remove the frequency 1000000


% Find the abrupt change of temperature 
A    = 6.4e-11; % Sectional area 
L    = max(dis);% distance 
Pcw0 = 4e-6;    % Incident light power   
a    = 0.046e-3;% Critical pump power 
g    = 5e-11;   % Brillouin gain peak 


figure;
for i=1:length(T)
    % Section 1
    if if_change == 1
        if i >= 1  & i <= s1 -1
            d = dis(1:s1-1);
        end    
        if i >= s1 & i <= e1
            d = dis(s1:e1);
        end         
        if i >= e1+1 & i <= s2-1
            d = dis(e1+1:s2-1);
        end          
        if i >= s2 & i<= e2
            d = dis(s2:e2);
        end            
        if i >= e2+1 & i<= length(T)
            d = dis(e2+1:length(T));
        end   
    else
        d = dis;   
    end
    [F,D]  = meshgrid(f,d);    

    % The relation between Brillouin strength and temperature is ：
    Psp_L = (2.04 + 0.007*T(i))/1000000000;

    P     = Psp_L*exp(a*D).*exp(+(g/A)*Pcw0*(exp(-a*D)-exp(-a*L))/a);
    fB    = VB2(i)/(1e6);% Center frequency at normal temperature , According to the above set of formulas, we can get 
    fBi   = 35;% bandwidth 
    Q     = 1./(1+((F-fB)/(fBi/2)).^2);    
    I     = P.*Q;

    mesh(D,F,I);
    hold on
    shading interp;
    alpha(0.75);     
    clear D F I d Psp_L P fB fBi Q
end

4. Simulation conclusion

    Go through the above steps , The linear relationship between Brillouin frequency shift and temperature can be verified .

    Other theories are basically the two papers you provided , So there is no further description here . here , We mainly derive and calculate the results of several parameters varying with temperature , Other parameters independent of the temperature are given directly .

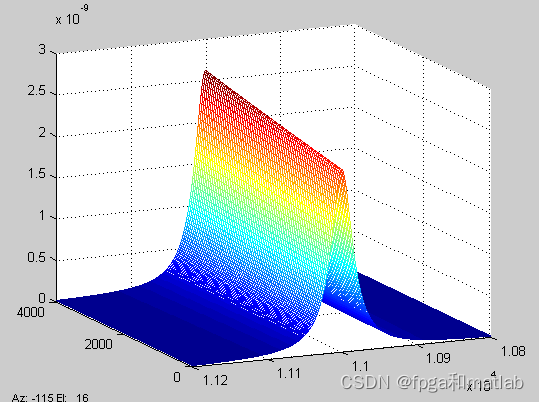
     When there is a temperature change , The simulation results are as follows ：

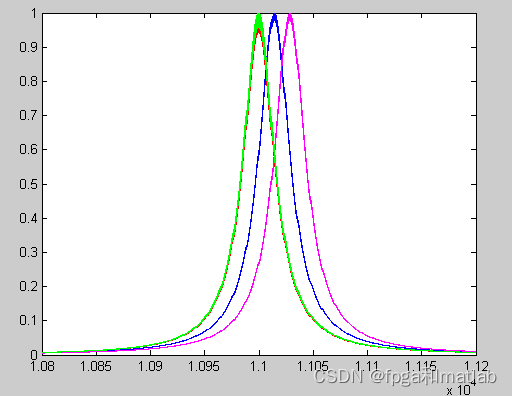
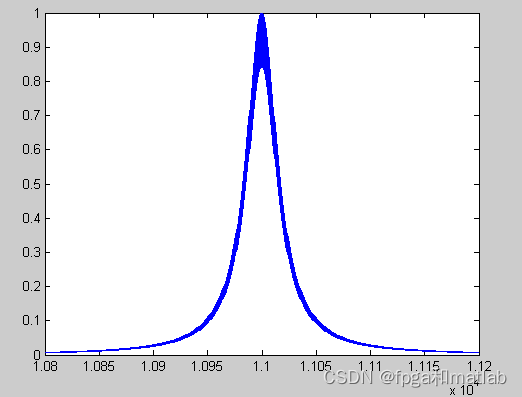
When there is no temperature difference .

A24-2