当前位置:网站首页>Halcon 用点来拟合平面
Halcon 用点来拟合平面
2022-06-12 05:30:00 【Σίσυφος1900】
一、简介
项目要求用多个点来拟合一个平面,然后再用其他平面上的点来计算这个点到平面的距离,halcon 有现成的拟合函数。
二、算子解释
*输入点云数据然后生成3D模型
gen_object_model_3d_from_points(X, Y, Z, ObjectModel3D)
* X, Y, Z 分别是点x、y、z方向上的集合
* ObjectModel3D 是输出的3D模型*拟合成想要的平面
fit_primitives_object_model_3d (ObjectModel3D, ['primitive_type','fitting_algorithm'], ['plane','least_squares_tukey'], ObjectModel3DOut)
*fit_primitives_object_model_3d( : : ObjectModel3D, ParamName, ParamValue : ObjectModel3DOut)
*ObjectModel3D:输入模型
*ParamName:拟合的参数 :fitting_algorithm, max_radius, min_radius, output_point_coord, output_xyz_mapping, primitive_type
*ParamValue:对应'primitive_type'------'cylinder'(圆柱体), 'sphere'(球体), 'plane'(平面)。对应'primitive_type'------'least_squares', 'least_squares_huber', 'least_squares_tukey'几种最小二乘法,这里选择plane和least_squares
*ObjectModel3DOut:输出的平面
三、代码演示
X:=[-0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04]
Y:=[-0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04]
Z:=[-0.0, -0.0, -0.0, -0.0, -0.1, -0.0, -0.0, -0.1, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, 0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0]
*输入点云数据然后生成3D模型
gen_object_model_3d_from_points(X, Y, Z, ObjectModel3D)
dev_open_window(0, 0, 512, 512, 'black', WindowHandle)
*拟合成想要的平面
fit_primitives_object_model_3d (ObjectModel3D, ['primitive_type','fitting_algorithm'], ['plane','least_squares_tukey'], ObjectModel3DOut)
*fit_primitives_object_model_3d( : : ObjectModel3D, ParamName, ParamValue : ObjectModel3DOut)
*ObjectModel3D:输入模型
*ParamName:拟合的参数 :fitting_algorithm, max_radius, min_radius, output_point_coord, output_xyz_mapping, primitive_type
*ParamValue:对应'primitive_type'------'cylinder'(圆柱体), 'sphere'(球体), 'plane'(平面)。对应'primitive_type'------'least_squares', 'least_squares_huber', 'least_squares_tukey'几种最小二乘法,这里选择plane和least_squares
*ObjectModel3DOut:输出的平面
visualize_object_model_3d (WindowHandle,[ObjectModel3D,ObjectModel3DOut], [],[], \
['color_0','color_1','alpha_1','disp_pose'], ['green','gray',0.5,'true'],'RectBOX', [], [], Pose)
*获取法向量,Normal的前三个数值就是单位法向量
get_object_model_3d_params (ObjectModel3DOut, 'primitive_parameter', Normals)
平面方程:ax+by+cz+d=0;
gen_object_model_3d_from_points(X, Y, Z, ObjectModel3D)
paraName:=['primitive_type', 'fitting_algorithm']
paraVal:=['plane', 'least_squares_tukey']
fit_primitives_object_model_3d(ObjectModel3D, ['primitive_type', 'fitting_algorithm'], ['plane', 'least_squares_tukey'], ObjectModel3DOut)
get_object_model_3d_params(ObjectModel3DOut, 'primitive_parameter', plane)
* 计算平面方程(a,b,c,d)
A:= plane[0]
B:= plane[1]
C:= plane[2]
D:= plane[3]
那么计算点到平面的距离就是:
Distance:=a*X + b*Y + c*Z - d
X:=[-0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04]
Y:=[-0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04]
Z:=[-0.0, -0.0, -0.0, -0.0, -0.1, -0.0, -0.0, -0.1, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, 0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0]
gen_object_model_3d_from_points(X, Y, Z, ObjectModel3D)
paraName:=['primitive_type', 'fitting_algorithm']
paraVal:=['plane', 'least_squares_tukey']
fit_primitives_object_model_3d(ObjectModel3D, ['primitive_type', 'fitting_algorithm'], ['plane', 'least_squares_tukey'], ObjectModel3DOut)
get_object_model_3d_params(ObjectModel3DOut, 'primitive_parameter', plane)
* 计算平面方程(a,b,c,d)
A:= plane[0]
B:= plane[1]
C:= plane[2]
D:= plane[3]
x:=[-0.04, -0.03, -0.02, -0.01]
y:=[-0.04, -0.04, -0.04, -0.04]
z:=[-0.0, -1.0, 10.0, 30.0]
Distance:=A*x +B*y + C*z - D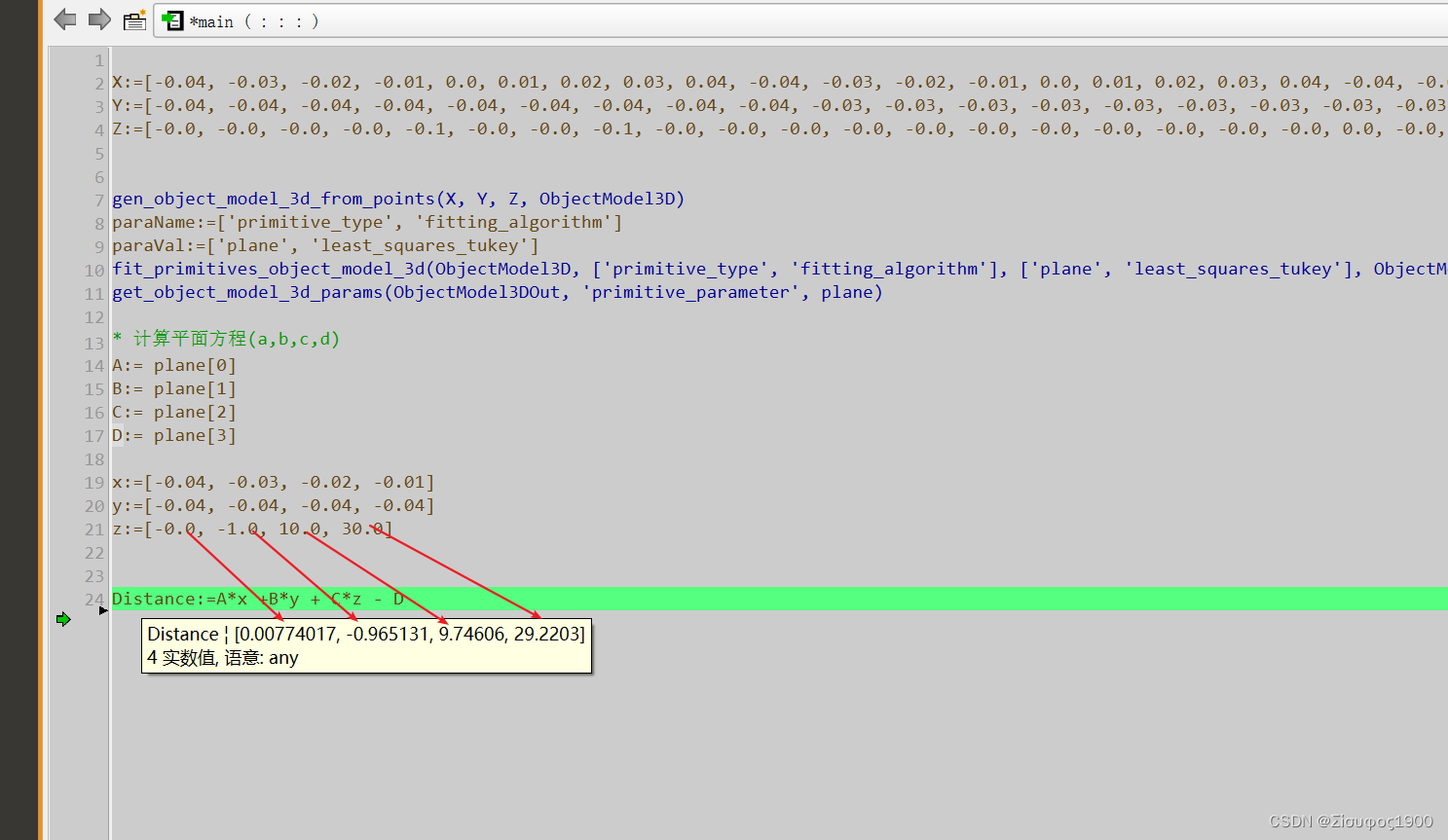
边栏推荐
- Calculation method notes for personal use
- The way to promote software test engineer
- Layer sublayer assigns values to the page elements of the parent layer to achieve the effect of transferring values to the page of the parent layer
- Wireshark filter rule
- Detailed tutorial on the use of yolov5 and training your own dataset with yolov5
- Matlab: halftone and dither conversion
- 第五讲:数据仓库搭建(三)
- 20000 word detailed reptile knowledge reserve, basic exercises of data collection and cleaning (I) reference answers to the first song
- 论文阅读_图神经网络GIN
- 个体工商户是不是法人企业
猜你喜欢

Abstract methods and interfaces

Pupanvr- an open source embedded NVR system (1)

16. 最接近的三數之和

Legal liabilities to be borne by the person in charge of the branch

beginning一款非常优秀的emlog主题v3.1,支持Emlog Pro

Performance test - performance test tool analysis

week7

Role and understanding of proc/cmdline

Performance test - GTI application service performance monitoring platform

Classes and objects, methods and encapsulation
随机推荐
Minigui3 runs on Hisilicon hi3520d/hi3531 platform
[C language] realize string interception function
Computer network connected but unable to access the Internet
Yolov5 realizes road crack detection
New knowledge today
Uview customer management JS
FPGA语法的细节
38. 外观数列
Role and understanding of proc/cmdline
分公司负责人需要承担的法律责任
49. ugly number
WiFi smartconfig implementation
Project requirements specification
How long is the company's registered capital subscribed
UBI details and JFFS2 square FS UBIFS
[getting to the bottom] five minutes to understand the combination evaluation model - fuzzy borde (taking the C question of the 2021 college students' numerical simulation national competition as an e
Legal liabilities to be borne by the person in charge of the branch
SQL transaction
20000 word detailed reptile knowledge reserve, basic exercises of data collection and cleaning (I) reference answers to the first song
Is the individual industrial and commercial door a legal person enterprise