Using Monte Carlo method to calculate pi

Ideas

The area of a square is ：
The area of the circle is ：
The area of a circle is... Larger than that of a square ：π / 4
Use Monte Carlo method to scatter points randomly in the square , The point falling in the circle / The point falling in the square （ All points ）, It's about equal to the area of the circle / The square area = π / 4

The code is implemented in the first quadrant 1/4 Circle as an example .

Code

import random
 
def count_pi(n):
    # Here we use 1/4 Circle writing code logic 
    i = 0
    count = 0
    # n  Is the total number of incoming points 
    while i < n:
        #  Randomly generated x,y coordinate 
        # random.random() Used to generate a 0 To 1 The number of random characters of : 0 <= n < 1.0
        x = random.random()
        y = random.random()
        #  If x square  + y square  < 1, Description in circle 
        if (pow(x, 2) + pow(y, 2)) < 1:
            count += 1
        i += 1
    # π The value of is ：4 * （ The point falling in the circle / Total point ）
    return 4 * (count / n)
 
 
pi = count_pi(100000)
print(pi)

Running results

function 100 Time , Average. .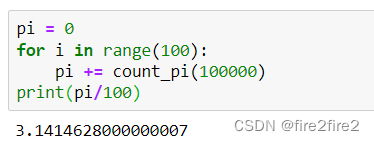

Mont · Carol's method （Monte Carlo method）, Also known as statistical simulation method , A kind of very important numerical calculation method guided by the theory of probability and statistics . It means using random numbers （ Or more common pseudo-random numbers ） To solve a lot of computational problems .