当前位置:网站首页>Luogu p4047 [jsoi2010] tribal division solution
Luogu p4047 [jsoi2010] tribal division solution
2022-07-03 14:27:00 【q779】
Luogu P4047 [JSOI2010] Tribal Division Answer key
Topic link :P4047 [JSOI2010] Tribal Division
The question :
Congcong's research found that , Wild islanders always live in groups , however , Not all the savages on the whole desert island belong to the same tribe , Wild people are always ganging up to form their own tribes , There are often fights between different tribes . It's just , It's all a mystery —— Congcong doesn't know how the tribes are distributed .
But the good news is , Congcong gets a map of the desert island . The map is marked n n n A place where savages live ( It can be regarded as coordinates on the plane ). We know , Savages of the same tribe always live nearby . We put the distance between the two tribes , It is defined as the distance between the two nearest settlements in the tribe . Congcong also got a meaningful message —— These savages are divided into k k k Tribes ! That's good news . Congcong hopes to mine the details of all tribes from this information . He is trying such an algorithm :
For any method of tribal division , Can find the distance between the two tribes , Congcong hopes to find a way to divide tribes , Keep the two nearest tribes as far away as possible .
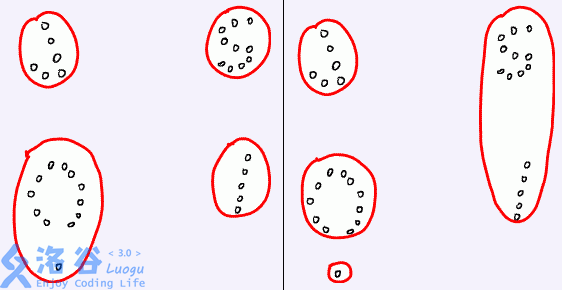
for example , The left figure below shows a good division , The picture on the right is not . Please program to help Congcong solve this problem .
about 100 % 100\% 100% The data of , Guarantee 2 ≤ k ≤ n ≤ 1 0 3 2 \leq k \leq n \leq 10^3 2≤k≤n≤103, 0 ≤ x , y ≤ 1 0 4 0 \leq x, y \leq 10^4 0≤x,y≤104.
The minimum distance is the maximum , One eye and two points
But here is a kruskal Solution method
Let's put the O ( n 2 ) O(n^2) O(n2) The edge is built
Then find the minimum spanning tree
Greedily divide the minimum spanning tree into k k k A connecting block
Concrete , We just merge the smallest edges of the tree in turn
Finally, a total of ( n − 1 ) − ( k − 1 ) = n − k (n-1)-(k-1) = n-k (n−1)−(k−1)=n−k side
So the answer is n − k + 1 n-k+1 n−k+1 The edge weight of the edge
Mouth paste a proof of correctness ( Maybe not very rigorous )
Consider counter evidence
Set an edge on the minimum spanning tree w 1 ( u , v ) w_1(u,v) w1(u,v) , Replace it with w 2 ( u , v ′ ) w_2(u,v^{\prime}) w2(u,v′) ( w 2 > w 1 w_2>w_1 w2>w1)
If w 1 w_1 w1 Will be merged and we merged w 2 w_2 w2 , It seems that there is no change
If w 1 w_1 w1 Will be merged and we didn't merge w 2 w_2 w2 ,
Then we must merge a ratio w 1 w_1 w1 Big side , And it is the edge on the minimum spanning tree
So the answer will be too big
If w 1 w_1 w1 Will not be merged and we merged w 2 w_2 w2 , There is no such situation .
If w 1 w_1 w1 Will not be merged and we did not merge w 2 w_2 w2 , No influence .
Time complexity O ( n 2 log n ) O(n^2 \log n) O(n2logn)
Code :
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <iomanip>
using namespace std;
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
#define N (int)(1e3+15)
#define M (int)(1e6+15)
#define pf(x) ((x)*(x))
struct Edge{
int u,v,w;}e[M];
int n,k,f[N],x[N],y[N],c[N],pos;
int find(int x){
return f[x]==x?x:f[x]=find(f[x]);}
void merge(int u,int v){
f[find(u)]=find(v);}
void addEdge(int u,int v,int w){
e[++pos]={
u,v,w};}
int dis(int i,int j){
return pf(x[i]-x[j])+pf(y[i]-y[j]);}
void kruskal()
{
sort(e+1,e+1+pos,[](Edge a,Edge b)
{
return a.w<b.w;
});
int cnt=0;
for(int i=1; i<=pos&&cnt<n; i++)
{
int u=e[i].u,v=e[i].v;
if(find(u)!=find(v))
{
merge(u,v);
c[++cnt]=e[i].w;
}
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
// freopen("check.in","r",stdin);
// freopen("check.out","w",stdout);
cin >> n >> k;
for(int i=1; i<=n; i++)
f[i]=i,cin >> x[i] >> y[i];
for(int i=1; i<=n; i++)
for(int j=1; j<i; j++)
addEdge(i,j,dis(i,j));
kruskal();
cout << fixed << setprecision(2);
cout << sqrt((double)c[n-k+1]) << '\n';
return 0;
}
Reprint please explain the source
边栏推荐
- Add ZABBIX calculation type itemcalculated items
- 556. The next larger element III
- Bibit pharmaceutical rushed to the scientific innovation board: annual revenue of 970000, loss of 137million, proposed to raise 2billion
- Leetcode(4)——尋找兩個正序數組的中比特數
- 关于回溯问题中的排列问题的思考(LeetCode46题与47题)
- 战略、战术(和 OKR)
- 虽然不一定最优秀,但一定是最努力的!
- Too many files with unapproved license
- 洛谷P5018 [NOIP2018 普及组] 对称二叉树 题解
- 洛谷P4047 [JSOI2010]部落划分 题解
猜你喜欢

puzzle(016.4)多米诺效应
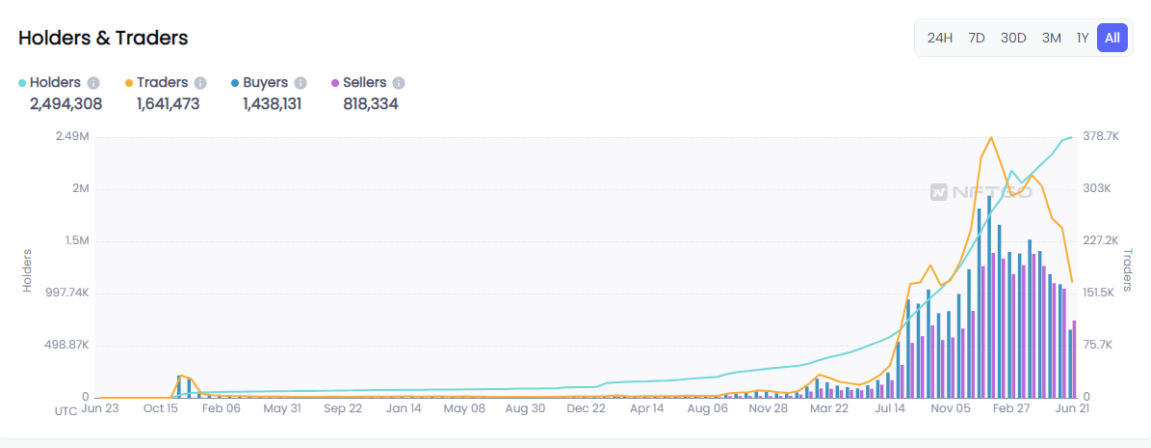
NFT新的契机,多媒体NFT聚合平台OKALEIDO即将上线

Programming language: the essence of type system
玖逸云黑免费无加密版本源码

Exercise 6-2 using functions to sum special A-string sequences

X86 assembly language - Notes from real mode to protected mode

Jiuyi cloud black free encryption free version source code
Thinking about the arrangement problem in the backtracking problem (leetcode questions 46 and 47)
Print. JS -- web page file printing

NPM install is stuck with various strange errors of node NPY
随机推荐
Zabbix添加Calculated items后保存页面成空白
Sendmail can't send mail and it's too slow to send. Solve it
Exercise 8-2 calculate the sum and difference of two numbers
7-22 tortoise and rabbit race (result oriented)
基因家族特征分析 - 染色体定位分析
NPM install is stuck with various strange errors of node NPY
Too many files with unapproved license
Print. JS -- web page file printing
Tailing rushes to the scientific and Technological Innovation Board: it plans to raise 1.3 billion, and Xiaomi Changjiang is the shareholder
Exercise 10-1 judge the three digits that meet the conditions
7-14 sum integer segments (C language)
ConstraintLayout 的使用
Understanding of closures
洛谷P5018 [NOIP2018 普及组] 对称二叉树 题解
洛谷P3065 [USACO12DEC]First! G 题解
Eight sorts
洛谷P4047 [JSOI2010]部落划分 题解
concat和concat_ws()区别及group_concat()和repeat()函数的使用
How Facebook moves instagram from AWS to its own server
2021年区域赛ICPC沈阳站J-Luggage Lock(代码简洁)