当前位置:网站首页>洛谷P4047 [JSOI2010]部落划分 题解
洛谷P4047 [JSOI2010]部落划分 题解
2022-07-03 14:15:00 【q779】
洛谷P4047 [JSOI2010]部落划分 题解
题目链接:P4047 [JSOI2010]部落划分
题意:
聪聪研究发现,荒岛野人总是过着群居的生活,但是,并不是整个荒岛上的所有野人都属于同一个部落,野人们总是拉帮结派形成属于自己的部落,不同的部落之间则经常发生争斗。只是,这一切都成为谜团了——聪聪根本就不知道部落究竟是如何分布的。
不过好消息是,聪聪得到了一份荒岛的地图。地图上标注了 n n n 个野人居住的地点(可以看作是平面上的坐标)。我们知道,同一个部落的野人总是生活在附近。我们把两个部落的距离,定义为部落中距离最近的那两个居住点的距离。聪聪还获得了一个有意义的信息——这些野人总共被分为了 k k k 个部落!这真是个好消息。聪聪希望从这些信息里挖掘出所有部落的详细信息。他正在尝试这样一种算法:
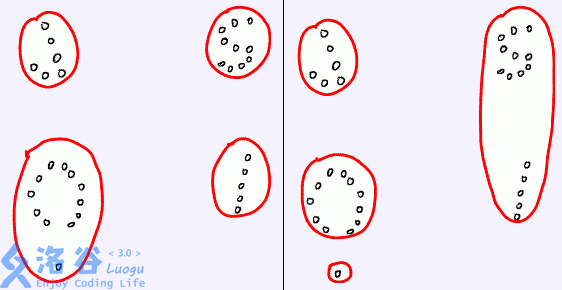
对于任意一种部落划分的方法,都能够求出两个部落之间的距离,聪聪希望求出一种部落划分的方法,使靠得最近的两个部落尽可能远离。
例如,下面的左图表示了一个好的划分,而右图则不是。请你编程帮助聪聪解决这个难题。
对于 100 % 100\% 100% 的数据,保证 2 ≤ k ≤ n ≤ 1 0 3 2 \leq k \leq n \leq 10^3 2≤k≤n≤103, 0 ≤ x , y ≤ 1 0 4 0 \leq x, y \leq 10^4 0≤x,y≤104。
最小距离最大,一眼二分
但是这里给出一个kruskal的解法
我们先把 O ( n 2 ) O(n^2) O(n2) 条边建出来
然后找到最小生成树
贪心地把最小生成树划分为 k k k 个连通块
具体的,我们只要依次合并树上最小边
最后一共合并掉 ( n − 1 ) − ( k − 1 ) = n − k (n-1)-(k-1) = n-k (n−1)−(k−1)=n−k 条边
所以答案就是第 n − k + 1 n-k+1 n−k+1 条边的边权
口糊一个正确性证明(可能不是很严谨)
考虑反证法
设最小生成树上的一条边 w 1 ( u , v ) w_1(u,v) w1(u,v) ,将其替换为 w 2 ( u , v ′ ) w_2(u,v^{\prime}) w2(u,v′) ( w 2 > w 1 w_2>w_1 w2>w1)
如果 w 1 w_1 w1 会被合并而我们合并了 w 2 w_2 w2 ,好像看不出什么变化
如果 w 1 w_1 w1 会被合并而我们没有合并 w 2 w_2 w2 ,
那么我们一定合并了一条比 w 1 w_1 w1 大的边,而且是最小生成树上的边
因此答案会偏大
如果 w 1 w_1 w1 不会被合并而我们合并了 w 2 w_2 w2 ,没有这种情况。
如果 w 1 w_1 w1 不会被合并而我们没有合并 w 2 w_2 w2 ,没影响。
时间复杂度 O ( n 2 log n ) O(n^2 \log n) O(n2logn)
代码:
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <iomanip>
using namespace std;
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
#define N (int)(1e3+15)
#define M (int)(1e6+15)
#define pf(x) ((x)*(x))
struct Edge{
int u,v,w;}e[M];
int n,k,f[N],x[N],y[N],c[N],pos;
int find(int x){
return f[x]==x?x:f[x]=find(f[x]);}
void merge(int u,int v){
f[find(u)]=find(v);}
void addEdge(int u,int v,int w){
e[++pos]={
u,v,w};}
int dis(int i,int j){
return pf(x[i]-x[j])+pf(y[i]-y[j]);}
void kruskal()
{
sort(e+1,e+1+pos,[](Edge a,Edge b)
{
return a.w<b.w;
});
int cnt=0;
for(int i=1; i<=pos&&cnt<n; i++)
{
int u=e[i].u,v=e[i].v;
if(find(u)!=find(v))
{
merge(u,v);
c[++cnt]=e[i].w;
}
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
// freopen("check.in","r",stdin);
// freopen("check.out","w",stdout);
cin >> n >> k;
for(int i=1; i<=n; i++)
f[i]=i,cin >> x[i] >> y[i];
for(int i=1; i<=n; i++)
for(int j=1; j<i; j++)
addEdge(i,j,dis(i,j));
kruskal();
cout << fixed << setprecision(2);
cout << sqrt((double)c[n-k+1]) << '\n';
return 0;
}
转载请说明出处
边栏推荐
- Solve the problem of dormitory router campus network sharing login
- 2021年区域赛ICPC沈阳站J-Luggage Lock(代码简洁)
- C library function - qsort()
- 常见问题之PHP——ldap_add(): Add: Undefined attribute type in
- 编程语言:类型系统的本质
- Exercise 10-8 recursive implementation of sequential output of integers
- 动态获取权限
- C language,%d% Difference between 2D%2d%02d
- 超简单手机地图开发
- 7-17 crawling worms (break exercise)
猜你喜欢

Exercise 9-3 plane vector addition
Scroll detection, so that the content in the lower right corner is not displayed at the top of the page, but is displayed as the mouse slides

X86 assembly language - Notes from real mode to protected mode
Fabric. JS document

Leetcode(4)——尋找兩個正序數組的中比特數
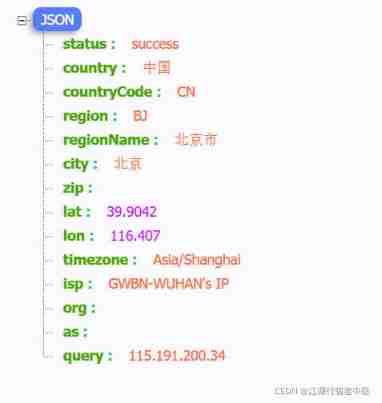
Interface for querying IP home
Exercise 8-8 moving letters

Similarities and differences between Allegro, OrCAD, net alias, port, off page connector and how to select them

MySQL multi table query subquery
JS first summary
随机推荐
[Jilin University] information sharing of postgraduate entrance examination and re examination
Too many files with unapproved license
Concat and concat_ Ws() differences and groups_ Use of concat() and repeat() functions
J-luggage lock of ICPC Shenyang station in 2021 regional games (simple code)
2021年区域赛ICPC沈阳站J-Luggage Lock(代码简洁)
7-15 calculation of PI
Exercise 8-7 string sorting
中国锂电池电解液行业市场专项调研报告(2022版)
Find the sum of the elements of each row of the matrix
Raft 协议
Zabbix添加Calculated items后保存页面成空白
Common mixins
Understand the application scenario and implementation mechanism of differential segment
Statistical capital consonants
SSH access control, blocking the IP when logging in repeatedly to prevent brute force cracking
SSH访问控制,多次失败登录即封掉IP,防止暴力破解
Find specified characters
Exercise 10-3 recursive implementation of exponential functions
Comprehensive evaluation of good-looking, easy-to-use and powerful handwriting note taking software: notability, goodnotes, marginnote, handwriting, notes writers, collanote, collanote, prodrafts, not
Doris学习笔记之数据表的创建