当前位置:网站首页>Leetcode (4) -- find the median of two positively ordered arrays
Leetcode (4) -- find the median of two positively ordered arrays
2022-07-03 14:11:00 【SmileGuy17】
Leetcode(4)—— Find the median of two positive arrays
subject
Given two sizes, they are m m m and n n n Positive order of ( From small to large ) Array n u m s 1 nums1 nums1 and n u m s 2 nums2 nums2. Please find and return the values of these two positive ordered arrays Median .
The time complexity of the algorithm should be O ( l o g ( m + n ) ) O(log (m+n)) O(log(m+n)).
Example 1:
Input :nums1 = [1,3], nums2 = [2]
Output :2.00000
explain : Merge array = [1,2,3] , Median 2
Example 2:
Input :nums1 = [1,2], nums2 = [3,4]
Output :2.50000
explain : Merge array = [1,2,3,4] , Median (2 + 3) / 2 = 2.5
Tips :
- nums1.length == m
- nums2.length == n
- 0 0 0 <= m <= 1000 1000 1000
- 0 0 0 <= n <= 1000 1000 1000
- 1 1 1 <= m + n <= 2000 2000 2000
- − 1 0 6 -10^6 −106 <= nums1[i], nums2[i] <= 1 0 6 10^6 106
Answer key
Other methods such as merging and searching will not be written , The time complexity is not up to the requirements and simple
Use merge mode , Merge two ordered arrays , Get a large ordered array . The element in the middle of a large ordered array , Is the median .
- There is no need to merge two ordered arrays , Just find the position of the median . Since the length of the two arrays is known , Therefore, the sum of the subscripts of the two arrays corresponding to the median is also known . Maintain two pointers , Initially, it points to the subscripts of two arrays 0 0 0 The location of , Move the pointer to the smaller value back one bit at a time ( If a pointer has reached the end of the array , Then you just need to move the pointer of another array ), Until you reach the median .
- Suppose that the lengths of two ordered arrays are m m m and n n n, How complex are the above two ideas ?
The time complexity of the first idea is O ( m + n ) O(m+n) O(m+n), The space complexity is O ( m + n ) O(m+n) O(m+n). Although the second idea can reduce the spatial complexity to O ( 1 ) O(1) O(1), But the time complexity is still O ( m + n ) O(m+n) O(m+n).
Method 1 : Two points search
Ideas
If time complexity is required log \log log, It's usually a binary search , This problem can also be realized by binary search .
According to the definition of the median , When m + n m+n m+n It's an odd number , The median is the... Of two ordered arrays ( m + n + 1 ) / 2 (m+n+1)/2 (m+n+1)/2 Elements , When m + n m+n m+n When it's even , The median is the... Of two ordered arrays ( m + n ) / 2 (m+n)/2 (m+n)/2 Elements and number ( m + n ) / 2 + 1 (m+n)/2+1 (m+n)/2+1 The average of the elements .
therefore , This problem can be transformed into : Find the... In two ordered arrays k k k Small number , When m + n m+n m+n It's an odd number , k k k by ( m + n ) / 2 + 1 (m+n)/2+1 (m+n)/2+1, When m + n m+n m+n When it's even , k k k by ( m + n ) / 2 (m+n)/2 (m+n)/2 and ( m + n ) / 2 + 1 (m+n)/2+1 (m+n)/2+1.
The specific algorithm is as follows :
Suppose two ordered arrays are A \text{A} A and B \text{B} B. To find number one k k k Elements , We can compare A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] and B [ k / 2 − 1 ] \text{B}[k/2-1] B[k/2−1], among / / / Represents integer division .
because A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] and B [ k / 2 − 1 ] \text{B}[k/2-1] B[k/2−1] Of front There were A [ 0 . . k / 2 − 2 ] \text{A}[0\,..\,k/2-2] A[0..k/2−2] and B [ 0 . . k / 2 − 2 ] \text{B}[0\,..\,k/2-2] B[0..k/2−2], namely k / 2 − 1 k/2-1 k/2−1 Elements , about A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] and B [ k / 2 − 1 ] \text{B}[k/2-1] B[k/2−1] The smaller of , At most, there will only be ( k / 2 − 1 ) + ( k / 2 − 1 ) ≤ k − 2 (k/2-1)+(k/2-1) \leq k-2 (k/2−1)+(k/2−1)≤k−2 It's smaller than that , Then it can't be the first k k k Small number .
So we Three situations can be summed up :
- If A [ k / 2 − 1 ] < B [ k / 2 − 1 ] \text{A}[k/2-1] < \text{B}[k/2-1] A[k/2−1]<B[k/2−1], More than A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] The number that is small or equal to is only A \text{A} A Before k / 2 − 1 k/2-1 k/2−1 Sum of numbers B \text{B} B Before k / 2 − 1 k/2-1 k/2−1 Number , I.e. ratio A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] Small number most Only k − 2 k-2 k−2 individual , therefore A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] It can't be number one k k k Number , A [ 0 ] \text{A}[0] A[0] To A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] It can't be the first k k k Number , A [ 0 ] \text{A}[0] A[0] To A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] You can exclude everything .
- If A [ k / 2 − 1 ] > B [ k / 2 − 1 ] \text{A}[k/2-1] > \text{B}[k/2-1] A[k/2−1]>B[k/2−1], be Can be ruled out B [ 0 ] \text{B}[0] B[0] To B [ k / 2 − 1 ] \text{B}[k/2-1] B[k/2−1].
- If A [ k / 2 − 1 ] = B [ k / 2 − 1 ] \text{A}[k/2-1] = \text{B}[k/2-1] A[k/2−1]=B[k/2−1], be It can be classified into the first case .

You can see , Compare A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] and B [ k / 2 − 1 ] \text{B}[k/2-1] B[k/2−1] after , Can be ruled out k / 2 k/2 k/2 The first can't be the first k k k Small number , The search scope is reduced by half . meanwhile , We The binary search will continue on the excluded new array , And according to the number of excluded numbers , Reduce k k k Value , This is because none of the numbers we exclude is greater than k k k Small number .
There are three situations that need special treatment :
- If A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] perhaps B [ k / 2 − 1 ] \text{B}[k/2-1] B[k/2−1] Transboundary , Then we can select the last element in the corresponding array . under these circumstances , We have to reduce... According to the number of exclusions k k k Value , Instead of directly k k k subtract k / 2 k/2 k/2.
- If an array is empty , Indicates that all elements in the array are excluded , We can directly return the... In another array k k k Small elements .
- If k = 1 k=1 k=1, We just need to return the minimum value of the first element of two arrays .
Example
An example is given to illustrate the above algorithm . Suppose two ordered arrays are as follows :
The lengths of the two ordered arrays are 4 4 4 and 9 9 9, The sum of the lengths is 13 13 13, The median is the... Of two ordered arrays 7 7 7 Elements , So we need to find the second k = 7 k=7 k=7 Elements .
Compare two ordered arrays with the subscript k / 2 − 1 = 2 k/2-1=2 k/2−1=2 Number of numbers , namely A [ 2 ] \text{A}[2] A[2] and B [ 2 ] \text{B}[2] B[2], This is shown below :
because A [ 2 ] > B [ 2 ] \text{A}[2] > \text{B}[2] A[2]>B[2], Thus eliminate B [ 0 ] \text{B}[0] B[0] To B [ 2 ] \text{B}[2] B[2], It's an array B \text{B} B Subscript offset (offset) Turn into 3 3 3, Simultaneous updating k k k Value : k = k − k / 2 = 4 k=k-k/2=4 k=k−k/2=4.
The next step is to find , Compare two ordered arrays with the subscript k / 2 − 1 = 1 k/2-1=1 k/2−1=1 Number of numbers , namely A [ 1 ] \text{A}[1] A[1] and B [ 4 ] \text{B}[4] B[4], This is shown below , The square brackets indicate the number that has been excluded .
because A [ 1 ] < B [ 4 ] \text{A}[1] < \text{B}[4] A[1]<B[4], Thus eliminate A [ 0 ] \text{A}[0] A[0] To A [ 1 ] \text{A}[1] A[1], It's an array A \text{A} A The subscript offset of becomes 2 2 2, Simultaneous updating k k k Value : k = k − k / 2 = 2 k=k-k/2=2 k=k−k/2=2.
The next step is to find , Compare two ordered arrays with the subscript k / 2 − 1 = 0 k/2-1=0 k/2−1=0 Number of numbers , Comparison A [ 2 ] \text{A}[2] A[2] and B [ 3 ] \text{B}[3] B[3], This is shown below , The square brackets indicate the number that has been excluded .
because A [ 2 ] = B [ 3 ] \text{A}[2]=\text{B}[3] A[2]=B[3], According to the previous rules , exclude A \text{A} A The elements in , Thus eliminate A [ 2 ] \text{A}[2] A[2], It's an array A \text{A} A The subscript offset of becomes 3 3 3, Simultaneous updating k k k Value : k = k − k / 2 = 1 k=k-k/2=1 k=k−k/2=1.
because k k k The value of the into 1 1 1, So compare the first number in the range of non excluded subscripts in two ordered arrays , The smaller number is the... Th k k k Number , because A [ 3 ] > B [ 3 ] \text{A}[3] > \text{B}[3] A[3]>B[3], So the first k k k The number is B [ 3 ] = 4 \text{B}[3]=4 B[3]=4.
Code implementation
Leetcode Official explanation :
class Solution {
public:
int getKthElement(const vector<int>& nums1, const vector<int>& nums2, int k) {
/* Main idea : To find number one k (k>1) Small elements , Then take it pivot1 = nums1[k/2-1] and pivot2 = nums2[k/2-1] Compare * there "/" To divide or divide * nums1 Less than equal to pivot1 The elements of nums1[0 .. k/2-2] total k/2-1 individual * nums2 Less than equal to pivot2 The elements of nums2[0 .. k/2-2] total k/2-1 individual * take pivot = min(pivot1, pivot2), Less than or equal to... In two arrays pivot The total number of elements will not exceed (k/2-1) + (k/2-1) <= k-2 individual * such pivot In itself, the biggest can only be the second k-1 Small elements * If pivot = pivot1, that nums1[0 .. k/2-1] It can't be the second k Small elements . Take all of these elements " Delete ", The rest as new nums1 Array * If pivot = pivot2, that nums2[0 .. k/2-1] It can't be the second k Small elements . Take all of these elements " Delete ", The rest as new nums2 Array * Because of us " Delete " Some elements were added ( These elements are better than k Small elements should be small ), So it needs to be modified k Value , Subtract the number of deletions */
int m = nums1.size();
int n = nums2.size();
int index1 = 0, index2 = 0;
while (true) {
// Boundary situation
if (index1 == m)
return nums2[index2 + k - 1];
if (index2 == n)
return nums1[index1 + k - 1];
if (k == 1)
return min(nums1[index1], nums2[index2]);
// Normal condition
int newIndex1 = min(index1 + k / 2 - 1, m - 1);
int newIndex2 = min(index2 + k / 2 - 1, n - 1);
int pivot1 = nums1[newIndex1];
int pivot2 = nums2[newIndex2];
if (pivot1 <= pivot2) {
k -= newIndex1 - index1 + 1;
index1 = newIndex1 + 1;
} else {
k -= newIndex2 - index2 + 1;
index2 = newIndex2 + 1;
}
}
}
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int totalLength = nums1.size() + nums2.size();
if (totalLength % 2 == 1)
return getKthElement(nums1, nums2, (totalLength + 1) / 2);
else
return (getKthElement(nums1, nums2, totalLength / 2) + getKthElement(nums1, nums2, totalLength / 2 + 1)) / 2.0;
}
};
Complexity analysis
Time complexity : O ( l o g ( m + n ) ) O(log(m+n)) O(log(m+n)), among m m m and n n n They are arrays nums 1 \textit{nums}_1 nums1 and nums 2 \textit{nums}_2 nums2 The length of . Initially there is k = ( m + n ) / 2 k=(m+n)/2 k=(m+n)/2 or k = ( m + n ) / 2 + 1 k=(m+n)/2+1 k=(m+n)/2+1, Each cycle can reduce the search range by half , So the time complexity is O ( log ( m + n ) ) O(\log(m+n)) O(log(m+n)).
Spatial complexity : O ( 1 ) O(1) O(1)
Method 2 : Two points search + Partition array
Ideas
In order to solve this problem by using partition , You need to understand 「 What is the role of the median 」, If you understand the role of median , It's very close to the answer .. In Statistics , The median is used to :
Divide a set into two subsets of equal length , The elements in one subset are always larger than those in the other .
First , In any position i i i take A \text{A} A Divided into two parts :
because A \text{A} A There is m m m Elements , So there is m + 1 m+1 m+1 A method of division ( i ∈ [ 0 , m ] i \in [0, m] i∈[0,m]).
len ( left_A ) = i , len ( right_A ) = m − i \text{len}(\text{left\_A}) = i, \text{len}(\text{right\_A}) = m - i len(left_A)=i,len(right_A)=m−i
Be careful : When i = 0 i = 0 i=0 when , left_A \text{left\_A} left_A For an empty set , And when i = m i = m i=m when , right_A \text{right\_A} right_A For an empty set .
In the same way , In any position j j j take B \text{B} B Divided into two parts :
take left_A \text{left\_A} left_A and left_B \text{left\_B} left_B Put in a collection , And will right_A \text{right\_A} right_A and right_B \text{right\_B} right_B Put into another set . Then name the two new sets left_part \text{left\_part} left_part and right_part \text{right\_part} right_part:
When A \text{A} A and B \text{B} B When the total length of is even , If you can confirm :
- len ( left_part ) = len ( right_part ) \text{len}(\text{left\_part}) = \text{len}(\text{right\_part}) len(left_part)=len(right_part)
- max ( left_part ) ≤ min ( right_part ) \max(\text{left\_part}) \leq \min(\text{right\_part}) max(left_part)≤min(right_part)
that , { A , B } \{\text{A}, \text{B}\} { A,B} All elements in have been divided into two parts of the same length , And the elements in the former part are always less than or equal to the elements in the latter part . The median is the average of the maximum value of the former part and the minimum value of the latter part :
median = max ( left _ part ) + min ( right _ part ) 2 \text{median} = \frac{\text{max}(\text{left}\_\text{part}) + \text{min}(\text{right}\_\text{part})}{2} median=2max(left_part)+min(right_part)
When A \text{A} A and B \text{B} B When the total length of is odd , If you can confirm :
- len ( left_part ) = len ( right_part ) + 1 \text{len}(\text{left\_part}) = \text{len}(\text{right\_part})+1 len(left_part)=len(right_part)+1
- max ( left_part ) ≤ min ( right_part ) \max(\text{left\_part}) \leq \min(\text{right\_part}) max(left_part)≤min(right_part)
that , { A , B } \{\text{A}, \text{B}\} { A,B} All elements in have been divided into two parts , The former part has one more element than the latter part , And the elements in the former part are always less than or equal to the elements in the latter part . The median is the maximum of the previous part :
median = max ( left _ part ) \text{median} = \text{max}(\text{left}\_\text{part}) median=max(left_part)
The first condition is different when the total length is even and odd , But you can combine the two situations . The second condition is the same when the total length is even and odd .
Make sure these two conditions , Just make sure that :
- i + j = m − i + n − j i + j = m - i + n - j i+j=m−i+n−j( When m + n m+n m+n For the even ) or i + j = m − i + n − j + 1 i + j = m - i + n - j + 1 i+j=m−i+n−j+1( When m + n m+n m+n It's odd ). To the left of the equal sign is the number of elements in the previous part , To the right of the equal sign is the number of elements in the latter part . take i i i and j j j Move all to the left of the equal sign , We can get it i + j = m + n + 1 2 i+j = \frac{m + n + 1}{2} i+j=2m+n+1. The score result here only retains the integer part .
- 0 ≤ i ≤ m 0 \leq i \leq m 0≤i≤m, 0 ≤ j ≤ n 0 \leq j \leq n 0≤j≤n. If we stipulate A \text{A} A Less than or equal to B \text{B} B The length of , namely m ≤ n m \leq n m≤n. This is for any i ∈ [ 0 , m ] i \in [0, m] i∈[0,m], There are j = m + n + 1 2 − i ∈ [ 0 , n ] j = \frac{m + n + 1}{2} - i \in [0, n] j=2m+n+1−i∈[0,n], So we're in [ 0 , m ] [0, m] [0,m] Enumeration within the scope of i i i And get the j j j, There is no need for additional properties .
- If A \text{A} A The length of , Then we just exchange A \text{A} A and B \text{B} B that will do .
- If m > n m > n m>n, So the conclusion is j j j It could be negative .
- B [ j − 1 ] ≤ A [ i ] \text{B}[j-1] \leq \text{A}[i] B[j−1]≤A[i] as well as A [ i − 1 ] ≤ B [ j ] \text{A}[i-1] \leq \text{B}[j] A[i−1]≤B[j], That is, the maximum value of the former part is less than or equal to the minimum value of the latter part .
To simplify the analysis , hypothesis A [ i − 1 ] , B [ j − 1 ] , A [ i ] , B [ j ] \text{A}[i-1], \text{B}[j-1], \text{A}[i], \text{B}[j] A[i−1],B[j−1],A[i],B[j] There is always . about i = 0 i=0 i=0、 i = m i=m i=m、 j = 0 j=0 j=0、 j = n j=n j=n Such critical conditions , We just need to stipulate A [ − 1 ] = B [ − 1 ] = − ∞ \text{A}[-1]=\text{B}[-1]=-\infty A[−1]=B[−1]=−∞, A [ m ] = B [ n ] = ∞ A[m]=\text{B}[n]=\infty A[m]=B[n]=∞ that will do . This is also more intuitive : When an array does not appear in the previous part , The corresponding value is negative infinity , It will not affect the maximum value of the previous part ; When an array does not appear in the latter part , The corresponding value is positive infinity , It will not affect the minimum value of the latter part .
So what we need to do is :
stay [ 0 , m ] [0, m] [0,m] Find i i i, bring :
B [ j − 1 ] ≤ A [ i ] \qquad \text{B}[j-1] \leq \text{A}[i] B[j−1]≤A[i] And A [ i − 1 ] ≤ B [ j ] \text{A}[i-1] \leq \text{B}[j] A[i−1]≤B[j], among j = m + n + 1 2 − i j = \frac{m + n + 1}{2} - i j=2m+n+1−i
We prove that it is equivalent to :
stay [ 0 , m ] [0, m] [0,m] Find the biggest in i i i, bring :
A [ i − 1 ] ≤ B [ j ] \qquad \text{A}[i-1] \leq \text{B}[j] A[i−1]≤B[j], among j = m + n + 1 2 − i j = \frac{m + n + 1}{2} - i j=2m+n+1−i
This is because :
- When i i i from 0 ∼ m 0 \sim m 0∼m When increasing , A [ i − 1 ] \text{A}[i-1] A[i−1] Increasing , B [ j ] \text{B}[j] B[j] Decline , So there must be a biggest i i i Satisfy A [ i − 1 ] ≤ B [ j ] \text{A}[i-1] \leq \text{B}[j] A[i−1]≤B[j];
- If i i i It's the biggest , It means that i + 1 i+1 i+1 dissatisfaction . take i + 1 i+1 i+1 You can get A [ i ] > B [ j − 1 ] \text{A}[i] > \text{B}[j-1] A[i]>B[j−1], That is to say B [ j − 1 ] < A [ i ] \text{B}[j - 1] < \text{A}[i] B[j−1]<A[i], Just before the equivalent transformation with us i i i The nature of is consistent ( Even better ).
So we can do something about i i i stay [ 0 , m ] [0, m] [0,m] Binary search on the interval of , Find the greatest satisfaction A [ i − 1 ] ≤ B [ j ] \text{A}[i-1] \leq \text{B}[j] A[i−1]≤B[j] Of i i i value , You get the method of division . here , Divide the maximum value in the previous element , And the minimum value of the elements after division , It can be used as the median of these two arrays .
Code implementation
Leetcode Official explanation :
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
if (nums1.size() > nums2.size()) {
return findMedianSortedArrays(nums2, nums1);
}
int m = nums1.size();
int n = nums2.size();
int left = 0, right = m;
// median1: The maximum of the previous part
// median2: The minimum of the latter part
int median1 = 0, median2 = 0;
while (left <= right) {
// The former part contains nums1[0 .. i-1] and nums2[0 .. j-1]
// The latter part contains nums1[i .. m-1] and nums2[j .. n-1]
int i = (left + right) / 2;
int j = (m + n + 1) / 2 - i;
// nums_im1, nums_i, nums_jm1, nums_j respectively nums1[i-1], nums1[i], nums2[j-1], nums2[j]
int nums_im1 = (i == 0 ? INT_MIN : nums1[i - 1]);
int nums_i = (i == m ? INT_MAX : nums1[i]);
int nums_jm1 = (j == 0 ? INT_MIN : nums2[j - 1]);
int nums_j = (j == n ? INT_MAX : nums2[j]);
if (nums_im1 <= nums_j) {
median1 = max(nums_im1, nums_jm1);
median2 = min(nums_i, nums_j);
left = i + 1;
} else {
right = i - 1;
}
}
return (m + n) % 2 == 0 ? (median1 + median2) / 2.0 : median1;
}
};
Complexity analysis
Time complexity : O ( log min ( m , n ) ) ) O(\log\min(m,n))) O(logmin(m,n))), among m m m and n n n They are arrays nums 1 \textit{nums}_1 nums1 and nums 2 \textit{nums}_2 nums2 The length of . The search interval is [ 0 , m ] [0, m] [0,m], The length of this interval will be reduced to half of the original after each cycle . therefore , Just execute log m \log m logm Secondary cycle . Since the number of operations in each cycle is constant , So the time complexity is O ( log m ) O(\log m) O(logm). Because we may need to exchange nums 1 \textit{nums}_1 nums1 and nums 2 \textit{nums}_2 nums2 bring m ≤ n m \leq n m≤n And we Only the shorter array is binary searched , So the time complexity is O ( log min ( m , n ) ) ) O(\log\min(m,n))) O(logmin(m,n))).
Spatial complexity : O ( 1 ) O(1) O(1)
边栏推荐
- simpleParallax. JS (create poor visual effects for website pictures)
- Qt学习25 布局管理器(四)
- jvm-对象生命周期
- Metal organic framework material zif-8 containing curcumin( [email protected] Nanoparticles) | nano metal organic framework carry
- 3D vision - 2 Introduction to pose estimation - openpose includes installation, compilation and use (single frame, real-time video)
- Exercise 10-6 recursively find Fabonacci sequence
- QT learning 21 standard dialog box in QT (Part 2)
- Exercise 8-7 string sorting
- Multi person collaborative data annotation based on Baidu brain easydata from scratch
- 7-10 calculate salary
猜你喜欢

jvm-类加载
常见问题之PHP——ldap_add(): Add: Undefined attribute type in
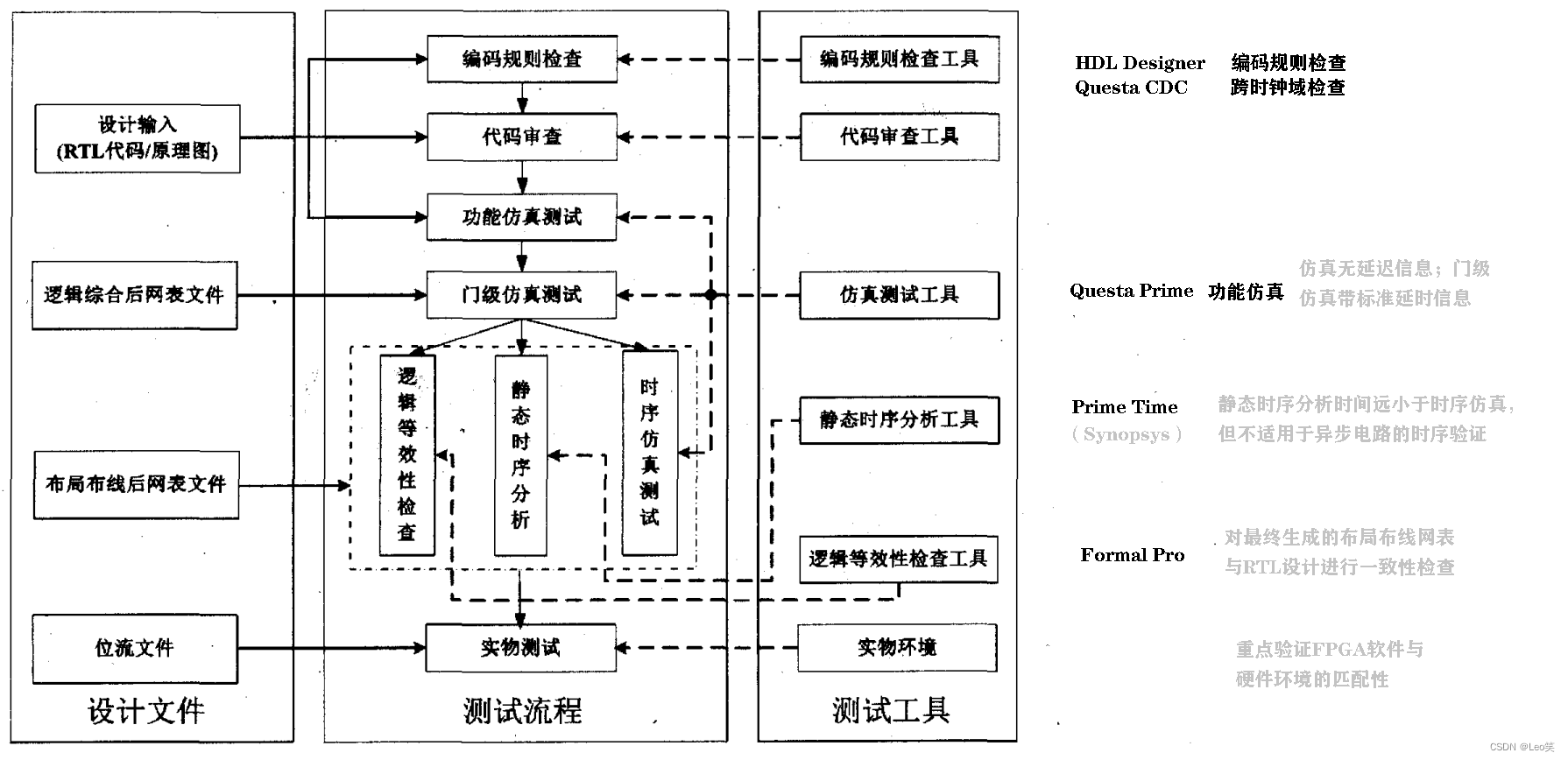
FPGA test method takes mentor tool as an example
Page generation QR code
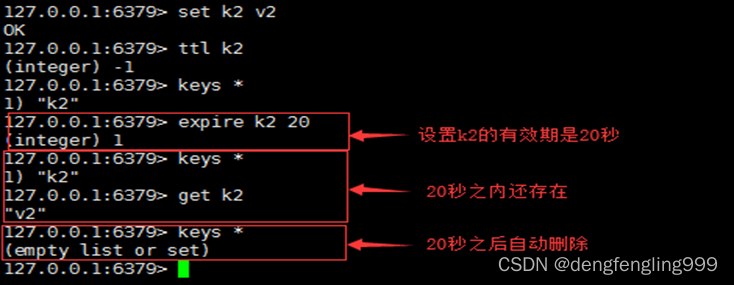
Redis:Redis的数据结构、key的操作命令
Global event bus

JVM class loading
Exercise 10-1 judge the three digits that meet the conditions

小项目(servelt+jsp+mysql+EL+JSTL)完成一个登录功能的Servlet,具有增删改查的操作。实现登录身份验证,防止非法登录,防止多点登录,记住用户名密码功能。
QT learning 19 standard dialog box in QT (top)
随机推荐
Exercise 10-1 judge the three digits that meet the conditions
Back to top implementation
Metal organic framework MOFs loaded with non steroidal anti-inflammatory drugs | zif-8 wrapped Prussian blue loaded quercetin (preparation method)
Qt学习24 布局管理器(三)
Invalid Z-index problem
Redis: operation command of string type data
金属有机骨架(MOFs)抗肿瘤药载体|PCN-223装载甲硝唑|UiO-66包载盐酸环丙沙星([email protected])
[clean up the extraordinary image of Disk C]
QT learning 21 standard dialog box in QT (Part 2)
page owner特性浅析
Exercise 6-6 use a function to output an integer in reverse order
7-10 calculate salary
RocksDB LRUCache
Qt学习17 对话框及其类型
Dynamic programming 01 knapsack and complete knapsack
JS new challenges
Uniapp skills - dom display and hiding
Metal organic framework (MOFs) antitumor drug carrier | pcn-223 loaded with metronidazole | uio-66 loaded with ciprofloxacin hydrochloride(
战略、战术(和 OKR)
Solve MySQL 1045 access denied for user 'root' @ 'localhost' (using password: yes)