当前位置:网站首页>Leetcode(4)——寻找两个正序数组的中位数
Leetcode(4)——寻找两个正序数组的中位数
2022-07-03 13:37:00 【SmileGuy17】
Leetcode(4)——寻找两个正序数组的中位数
题目
给定两个大小分别为 m m m 和 n n n 的正序(从小到大)数组 n u m s 1 nums1 nums1 和 n u m s 2 nums2 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O ( l o g ( m + n ) ) O(log (m+n)) O(log(m+n))。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
提示:
- nums1.length == m
- nums2.length == n
- 0 0 0 <= m <= 1000 1000 1000
- 0 0 0 <= n <= 1000 1000 1000
- 1 1 1 <= m + n <= 2000 2000 2000
- − 1 0 6 -10^6 −106 <= nums1[i], nums2[i] <= 1 0 6 10^6 106
题解
合并再查找等其他方法就不写了,时间复杂度达不到要求且简单
使用归并的方式,合并两个有序数组,得到一个大的有序数组。大的有序数组的中间位置的元素,即为中位数。
- 不需要合并两个有序数组,只要找到中位数的位置即可。由于两个数组的长度已知,因此中位数对应的两个数组的下标之和也是已知的。维护两个指针,初始时分别指向两个数组的下标 0 0 0 的位置,每次将指向较小值的指针后移一位(如果一个指针已经到达数组末尾,则只需要移动另一个数组的指针),直到到达中位数的位置。
- 假设两个有序数组的长度分别为 m m m 和 n n n,上述两种思路的复杂度如何?
第一种思路的时间复杂度是 O ( m + n ) O(m+n) O(m+n),空间复杂度是 O ( m + n ) O(m+n) O(m+n)。第二种思路虽然可以将空间复杂度降到 O ( 1 ) O(1) O(1),但是时间复杂度仍是 O ( m + n ) O(m+n) O(m+n)。
方法一:二分查找
思路
如果对时间复杂度的要求有 log \log log,通常都需要用到二分查找,这道题也可以通过二分查找实现。
根据中位数的定义,当 m + n m+n m+n 是奇数时,中位数是两个有序数组中的第 ( m + n + 1 ) / 2 (m+n+1)/2 (m+n+1)/2 个元素,当 m + n m+n m+n 是偶数时,中位数是两个有序数组中的第 ( m + n ) / 2 (m+n)/2 (m+n)/2 个元素和第 ( m + n ) / 2 + 1 (m+n)/2+1 (m+n)/2+1 个元素的平均值。
因此,这道题可以转化成:寻找两个有序数组中的第 k k k 小的数,当其中 m + n m+n m+n 是奇数时, k k k 为 ( m + n ) / 2 + 1 (m+n)/2+1 (m+n)/2+1,当其中 m + n m+n m+n 是偶数时, k k k 为 ( m + n ) / 2 (m+n)/2 (m+n)/2 和 ( m + n ) / 2 + 1 (m+n)/2+1 (m+n)/2+1。
具体算法思路如下:
假设两个有序数组分别是 A \text{A} A 和 B \text{B} B。要找到第 k k k 个元素,我们可以比较 A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] 和 B [ k / 2 − 1 ] \text{B}[k/2-1] B[k/2−1],其中 / / / 表示整数除法。
由于 A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] 和 B [ k / 2 − 1 ] \text{B}[k/2-1] B[k/2−1] 的前面分别有 A [ 0 . . k / 2 − 2 ] \text{A}[0\,..\,k/2-2] A[0..k/2−2] 和 B [ 0 . . k / 2 − 2 ] \text{B}[0\,..\,k/2-2] B[0..k/2−2],即 k / 2 − 1 k/2-1 k/2−1 个元素,对于 A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] 和 B [ k / 2 − 1 ] \text{B}[k/2-1] B[k/2−1] 中的较小值,最多只会有 ( k / 2 − 1 ) + ( k / 2 − 1 ) ≤ k − 2 (k/2-1)+(k/2-1) \leq k-2 (k/2−1)+(k/2−1)≤k−2 个元素比它小,那么它就不能是第 k k k 小的数了。
因此我们可以归纳出三种情况:
- 如果 A [ k / 2 − 1 ] < B [ k / 2 − 1 ] \text{A}[k/2-1] < \text{B}[k/2-1] A[k/2−1]<B[k/2−1],则比 A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] 小或等于的数最多只有 A \text{A} A 的前 k / 2 − 1 k/2-1 k/2−1 个数和 B \text{B} B 的前 k / 2 − 1 k/2-1 k/2−1 个数,即比 A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] 小的数最多只有 k − 2 k-2 k−2 个,因此 A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] 不可能是第 k k k 个数, A [ 0 ] \text{A}[0] A[0] 到 A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] 也都不可能是第 k k k 个数, A [ 0 ] \text{A}[0] A[0] 到 A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] 可以全部排除。
- 如果 A [ k / 2 − 1 ] > B [ k / 2 − 1 ] \text{A}[k/2-1] > \text{B}[k/2-1] A[k/2−1]>B[k/2−1],则可以排除 B [ 0 ] \text{B}[0] B[0] 到 B [ k / 2 − 1 ] \text{B}[k/2-1] B[k/2−1]。
- 如果 A [ k / 2 − 1 ] = B [ k / 2 − 1 ] \text{A}[k/2-1] = \text{B}[k/2-1] A[k/2−1]=B[k/2−1],则可以归入第一种情况处理。

可以看到,比较 A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] 和 B [ k / 2 − 1 ] \text{B}[k/2-1] B[k/2−1] 之后,可以排除 k / 2 k/2 k/2 个不可能是第 k k k 小的数,查找范围缩小了一半。同时,我们将在排除后的新数组上继续进行二分查找,并且根据我们排除数的个数,减少 k k k 的值,这是因为我们排除的数都不大于第 k k k 小的数。
有以下三种情况需要特殊处理:
- 如果 A [ k / 2 − 1 ] \text{A}[k/2-1] A[k/2−1] 或者 B [ k / 2 − 1 ] \text{B}[k/2-1] B[k/2−1] 越界,那么我们可以选取对应数组中的最后一个元素。在这种情况下,我们必须根据排除数的个数减少 k k k 的值,而不能直接将 k k k 减去 k / 2 k/2 k/2。
- 如果一个数组为空,说明该数组中的所有元素都被排除,我们可以直接返回另一个数组中第 k k k 小的元素。
- 如果 k = 1 k=1 k=1,我们只要返回两个数组首元素的最小值即可。
例子
用一个例子说明上述算法。假设两个有序数组如下:
两个有序数组的长度分别是 4 4 4 和 9 9 9,长度之和是 13 13 13,中位数是两个有序数组中的第 7 7 7 个元素,因此需要找到第 k = 7 k=7 k=7 个元素。
比较两个有序数组中下标为 k / 2 − 1 = 2 k/2-1=2 k/2−1=2 的数,即 A [ 2 ] \text{A}[2] A[2] 和 B [ 2 ] \text{B}[2] B[2],如下面所示:
由于 A [ 2 ] > B [ 2 ] \text{A}[2] > \text{B}[2] A[2]>B[2],因此排除 B [ 0 ] \text{B}[0] B[0] 到 B [ 2 ] \text{B}[2] B[2],即数组 B \text{B} B 的下标偏移(offset)变为 3 3 3,同时更新 k k k 的值: k = k − k / 2 = 4 k=k-k/2=4 k=k−k/2=4。
下一步寻找,比较两个有序数组中下标为 k / 2 − 1 = 1 k/2-1=1 k/2−1=1 的数,即 A [ 1 ] \text{A}[1] A[1] 和 B [ 4 ] \text{B}[4] B[4],如下面所示,其中方括号部分表示已经被排除的数。
由于 A [ 1 ] < B [ 4 ] \text{A}[1] < \text{B}[4] A[1]<B[4],因此排除 A [ 0 ] \text{A}[0] A[0] 到 A [ 1 ] \text{A}[1] A[1],即数组 A \text{A} A 的下标偏移变为 2 2 2,同时更新 k k k 的值: k = k − k / 2 = 2 k=k-k/2=2 k=k−k/2=2。
下一步寻找,比较两个有序数组中下标为 k / 2 − 1 = 0 k/2-1=0 k/2−1=0 的数,即比较 A [ 2 ] \text{A}[2] A[2] 和 B [ 3 ] \text{B}[3] B[3],如下面所示,其中方括号部分表示已经被排除的数。
由于 A [ 2 ] = B [ 3 ] \text{A}[2]=\text{B}[3] A[2]=B[3],根据之前的规则,排除 A \text{A} A 中的元素,因此排除 A [ 2 ] \text{A}[2] A[2],即数组 A \text{A} A 的下标偏移变为 3 3 3,同时更新 k k k 的值: k = k − k / 2 = 1 k=k-k/2=1 k=k−k/2=1。
由于 k k k 的值变成 1 1 1,因此比较两个有序数组中的未排除下标范围内的第一个数,其中较小的数即为第 k k k 个数,由于 A [ 3 ] > B [ 3 ] \text{A}[3] > \text{B}[3] A[3]>B[3],因此第 k k k 个数是 B [ 3 ] = 4 \text{B}[3]=4 B[3]=4。
代码实现
Leetcode 官方题解:
class Solution {
public:
int getKthElement(const vector<int>& nums1, const vector<int>& nums2, int k) {
/* 主要思路:要找到第 k (k>1) 小的元素,那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较 * 这里的 "/" 表示整除 * nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个 * nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个 * 取 pivot = min(pivot1, pivot2),两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个 * 这样 pivot 本身最大也只能是第 k-1 小的元素 * 如果 pivot = pivot1,那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums1 数组 * 如果 pivot = pivot2,那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums2 数组 * 由于我们 "删除" 了一些元素(这些元素都比第 k 小的元素要小),因此需要修改 k 的值,减去删除的数的个数 */
int m = nums1.size();
int n = nums2.size();
int index1 = 0, index2 = 0;
while (true) {
// 边界情况
if (index1 == m)
return nums2[index2 + k - 1];
if (index2 == n)
return nums1[index1 + k - 1];
if (k == 1)
return min(nums1[index1], nums2[index2]);
// 正常情况
int newIndex1 = min(index1 + k / 2 - 1, m - 1);
int newIndex2 = min(index2 + k / 2 - 1, n - 1);
int pivot1 = nums1[newIndex1];
int pivot2 = nums2[newIndex2];
if (pivot1 <= pivot2) {
k -= newIndex1 - index1 + 1;
index1 = newIndex1 + 1;
} else {
k -= newIndex2 - index2 + 1;
index2 = newIndex2 + 1;
}
}
}
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int totalLength = nums1.size() + nums2.size();
if (totalLength % 2 == 1)
return getKthElement(nums1, nums2, (totalLength + 1) / 2);
else
return (getKthElement(nums1, nums2, totalLength / 2) + getKthElement(nums1, nums2, totalLength / 2 + 1)) / 2.0;
}
};
复杂度分析
时间复杂度: O ( l o g ( m + n ) ) O(log(m+n)) O(log(m+n)),其中 m m m 和 n n n 分别是数组 nums 1 \textit{nums}_1 nums1 和 nums 2 \textit{nums}_2 nums2 的长度。初始时有 k = ( m + n ) / 2 k=(m+n)/2 k=(m+n)/2 或 k = ( m + n ) / 2 + 1 k=(m+n)/2+1 k=(m+n)/2+1,每一轮循环可以将查找范围减少一半,因此时间复杂度是 O ( log ( m + n ) ) O(\log(m+n)) O(log(m+n))。
空间复杂度: O ( 1 ) O(1) O(1)
方法二:二分查找+划分数组
思路
为了使用划分的方法解决这个问题,需要理解「中位数的作用是什么」,如果理解了中位数的划分作用,就很接近答案了。。在统计中,中位数被用来:
将一个集合划分为两个长度相等的子集,其中一个子集中的元素总是大于另一个子集中的元素。
首先,在任意位置 i i i 将 A \text{A} A 划分成两个部分:
由于 A \text{A} A 中有 m m m 个元素, 所以有 m + 1 m+1 m+1 种划分的方法( i ∈ [ 0 , m ] i \in [0, m] i∈[0,m])。
len ( left_A ) = i , len ( right_A ) = m − i \text{len}(\text{left\_A}) = i, \text{len}(\text{right\_A}) = m - i len(left_A)=i,len(right_A)=m−i
注意:当 i = 0 i = 0 i=0 时, left_A \text{left\_A} left_A 为空集, 而当 i = m i = m i=m 时, right_A \text{right\_A} right_A 为空集。
采用同样的方式,在任意位置 j j j 将 B \text{B} B 划分成两个部分:
将 left_A \text{left\_A} left_A 和 left_B \text{left\_B} left_B 放入一个集合,并将 right_A \text{right\_A} right_A 和 right_B \text{right\_B} right_B 放入另一个集合。 再把这两个新的集合分别命名为 left_part \text{left\_part} left_part 和 right_part \text{right\_part} right_part:
当 A \text{A} A 和 B \text{B} B 的总长度是偶数时,如果可以确认:
- len ( left_part ) = len ( right_part ) \text{len}(\text{left\_part}) = \text{len}(\text{right\_part}) len(left_part)=len(right_part)
- max ( left_part ) ≤ min ( right_part ) \max(\text{left\_part}) \leq \min(\text{right\_part}) max(left_part)≤min(right_part)
那么, { A , B } \{\text{A}, \text{B}\} { A,B} 中的所有元素已经被划分为相同长度的两个部分,且前一部分中的元素总是小于或等于后一部分中的元素。中位数就是前一部分的最大值和后一部分的最小值的平均值:
median = max ( left _ part ) + min ( right _ part ) 2 \text{median} = \frac{\text{max}(\text{left}\_\text{part}) + \text{min}(\text{right}\_\text{part})}{2} median=2max(left_part)+min(right_part)
当 A \text{A} A 和 B \text{B} B 的总长度是奇数时,如果可以确认:
- len ( left_part ) = len ( right_part ) + 1 \text{len}(\text{left\_part}) = \text{len}(\text{right\_part})+1 len(left_part)=len(right_part)+1
- max ( left_part ) ≤ min ( right_part ) \max(\text{left\_part}) \leq \min(\text{right\_part}) max(left_part)≤min(right_part)
那么, { A , B } \{\text{A}, \text{B}\} { A,B} 中的所有元素已经被划分为两个部分,前一部分比后一部分多一个元素,且前一部分中的元素总是小于或等于后一部分中的元素。中位数就是前一部分的最大值:
median = max ( left _ part ) \text{median} = \text{max}(\text{left}\_\text{part}) median=max(left_part)
第一个条件对于总长度是偶数和奇数的情况有所不同,但是可以将两种情况合并。第二个条件对于总长度是偶数和奇数的情况是一样的。
要确保这两个条件,只需要保证:
- i + j = m − i + n − j i + j = m - i + n - j i+j=m−i+n−j(当 m + n m+n m+n 为偶数)或 i + j = m − i + n − j + 1 i + j = m - i + n - j + 1 i+j=m−i+n−j+1(当 m + n m+n m+n 为奇数)。等号左侧为前一部分的元素个数,等号右侧为后一部分的元素个数。将 i i i 和 j j j 全部移到等号左侧,我们就可以得到 i + j = m + n + 1 2 i+j = \frac{m + n + 1}{2} i+j=2m+n+1。这里的分数结果只保留整数部分。
- 0 ≤ i ≤ m 0 \leq i \leq m 0≤i≤m, 0 ≤ j ≤ n 0 \leq j \leq n 0≤j≤n。如果我们规定 A \text{A} A 的长度小于等于 B \text{B} B 的长度,即 m ≤ n m \leq n m≤n。这样对于任意的 i ∈ [ 0 , m ] i \in [0, m] i∈[0,m],都有 j = m + n + 1 2 − i ∈ [ 0 , n ] j = \frac{m + n + 1}{2} - i \in [0, n] j=2m+n+1−i∈[0,n],那么我们在 [ 0 , m ] [0, m] [0,m] 的范围内枚举 i i i 并得到 j j j,就不需要额外的性质了。
- 如果 A \text{A} A 的长度较大,那么我们只要交换 A \text{A} A 和 B \text{B} B 即可。
- 如果 m > n m > n m>n,那么得出的 j j j 有可能是负数。
- B [ j − 1 ] ≤ A [ i ] \text{B}[j-1] \leq \text{A}[i] B[j−1]≤A[i] 以及 A [ i − 1 ] ≤ B [ j ] \text{A}[i-1] \leq \text{B}[j] A[i−1]≤B[j],即前一部分的最大值小于等于后一部分的最小值。
为了简化分析,假设 A [ i − 1 ] , B [ j − 1 ] , A [ i ] , B [ j ] \text{A}[i-1], \text{B}[j-1], \text{A}[i], \text{B}[j] A[i−1],B[j−1],A[i],B[j] 总是存在。对于 i = 0 i=0 i=0、 i = m i=m i=m、 j = 0 j=0 j=0、 j = n j=n j=n 这样的临界条件,我们只需要规定 A [ − 1 ] = B [ − 1 ] = − ∞ \text{A}[-1]=\text{B}[-1]=-\infty A[−1]=B[−1]=−∞, A [ m ] = B [ n ] = ∞ A[m]=\text{B}[n]=\infty A[m]=B[n]=∞ 即可。这也是比较直观的:当一个数组不出现在前一部分时,对应的值为负无穷,就不会对前一部分的最大值产生影响;当一个数组不出现在后一部分时,对应的值为正无穷,就不会对后一部分的最小值产生影响。
所以我们需要做的是:
在 [ 0 , m ] [0, m] [0,m] 中找到 i i i,使得:
B [ j − 1 ] ≤ A [ i ] \qquad \text{B}[j-1] \leq \text{A}[i] B[j−1]≤A[i] 且 A [ i − 1 ] ≤ B [ j ] \text{A}[i-1] \leq \text{B}[j] A[i−1]≤B[j],其中 j = m + n + 1 2 − i j = \frac{m + n + 1}{2} - i j=2m+n+1−i
我们证明它等价于:
在 [ 0 , m ] [0, m] [0,m] 中找到最大的 i i i,使得:
A [ i − 1 ] ≤ B [ j ] \qquad \text{A}[i-1] \leq \text{B}[j] A[i−1]≤B[j],其中 j = m + n + 1 2 − i j = \frac{m + n + 1}{2} - i j=2m+n+1−i
这是因为:
- 当 i i i 从 0 ∼ m 0 \sim m 0∼m 递增时, A [ i − 1 ] \text{A}[i-1] A[i−1] 递增, B [ j ] \text{B}[j] B[j] 递减,所以一定存在一个最大的 i i i 满足 A [ i − 1 ] ≤ B [ j ] \text{A}[i-1] \leq \text{B}[j] A[i−1]≤B[j];
- 如果 i i i 是最大的,那么说明 i + 1 i+1 i+1 不满足。将 i + 1 i+1 i+1 带入可以得到 A [ i ] > B [ j − 1 ] \text{A}[i] > \text{B}[j-1] A[i]>B[j−1],也就是 B [ j − 1 ] < A [ i ] \text{B}[j - 1] < \text{A}[i] B[j−1]<A[i],就和我们进行等价变换前 i i i 的性质一致了(甚至还要更好)。
因此我们可以对 i i i 在 [ 0 , m ] [0, m] [0,m] 的区间上进行二分搜索,找到最大的满足 A [ i − 1 ] ≤ B [ j ] \text{A}[i-1] \leq \text{B}[j] A[i−1]≤B[j] 的 i i i 值,就得到了划分的方法。此时,划分前一部分元素中的最大值,以及划分后一部分元素中的最小值,才可能作为就是这两个数组的中位数。
代码实现
Leetcode 官方题解:
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
if (nums1.size() > nums2.size()) {
return findMedianSortedArrays(nums2, nums1);
}
int m = nums1.size();
int n = nums2.size();
int left = 0, right = m;
// median1:前一部分的最大值
// median2:后一部分的最小值
int median1 = 0, median2 = 0;
while (left <= right) {
// 前一部分包含 nums1[0 .. i-1] 和 nums2[0 .. j-1]
// 后一部分包含 nums1[i .. m-1] 和 nums2[j .. n-1]
int i = (left + right) / 2;
int j = (m + n + 1) / 2 - i;
// nums_im1, nums_i, nums_jm1, nums_j 分别表示 nums1[i-1], nums1[i], nums2[j-1], nums2[j]
int nums_im1 = (i == 0 ? INT_MIN : nums1[i - 1]);
int nums_i = (i == m ? INT_MAX : nums1[i]);
int nums_jm1 = (j == 0 ? INT_MIN : nums2[j - 1]);
int nums_j = (j == n ? INT_MAX : nums2[j]);
if (nums_im1 <= nums_j) {
median1 = max(nums_im1, nums_jm1);
median2 = min(nums_i, nums_j);
left = i + 1;
} else {
right = i - 1;
}
}
return (m + n) % 2 == 0 ? (median1 + median2) / 2.0 : median1;
}
};
复杂度分析
时间复杂度: O ( log min ( m , n ) ) ) O(\log\min(m,n))) O(logmin(m,n))),其中 m m m 和 n n n 分别是数组 nums 1 \textit{nums}_1 nums1 和 nums 2 \textit{nums}_2 nums2 的长度。查找的区间是 [ 0 , m ] [0, m] [0,m],而该区间的长度在每次循环之后都会减少为原来的一半。所以,只需要执行 log m \log m logm 次循环。由于每次循环中的操作次数是常数,所以时间复杂度为 O ( log m ) O(\log m) O(logm)。由于我们可能需要交换 nums 1 \textit{nums}_1 nums1 和 nums 2 \textit{nums}_2 nums2 使得 m ≤ n m \leq n m≤n 且我们只对较短的数组进行了二分查找,因此时间复杂度是 O ( log min ( m , n ) ) ) O(\log\min(m,n))) O(logmin(m,n)))。
空间复杂度: O ( 1 ) O(1) O(1)
边栏推荐
- jvm-运行时数据区
- [bw16 application] instructions for firmware burning of Anxin Ke bw16 module and development board update
- Qt学习19 Qt 中的标准对话框(上)
- js . Find the first palindrome string in the array
- Scroll detection, so that the content in the lower right corner is not displayed at the top of the page, but is displayed as the mouse slides
- How to delete an attribute or method of an object
- 可编程逻辑器件软件测试
- MySQL 数据处理值增删改
- GoLand 2021.2 configure go (go1.17.6)
- Current situation, analysis and prediction of information and innovation industry
猜你喜欢
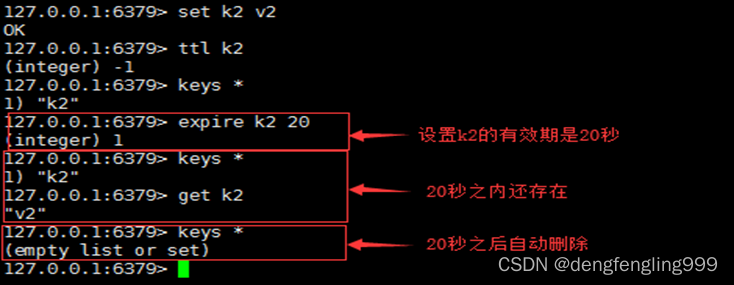
Redis: redis data structure and key operation commands
Metal organic framework MOFs loaded with non steroidal anti-inflammatory drugs | zif-8 wrapped Prussian blue loaded quercetin (preparation method)

好看、好用、强大的手写笔记软件综合评测:Notability、GoodNotes、MarginNote、随手写、Notes Writers、CollaNote、CollaNote、Prodrafts、Noteshelf、FlowUs、OneNote、苹果备忘录
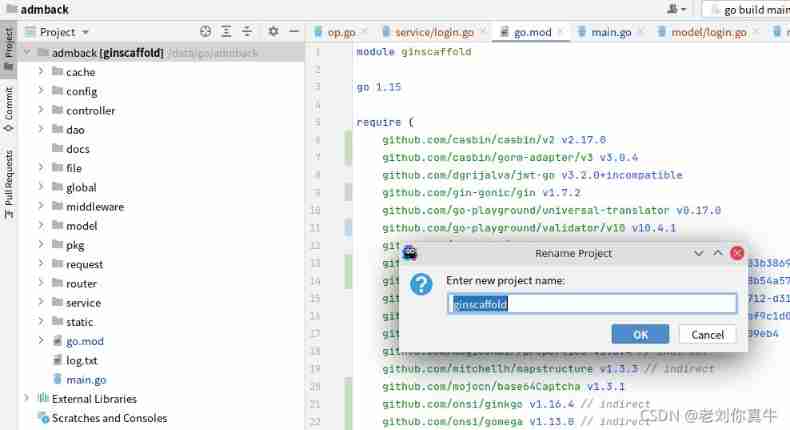
GoLand 2021.1: rename the go project
TS code automatically generates JS
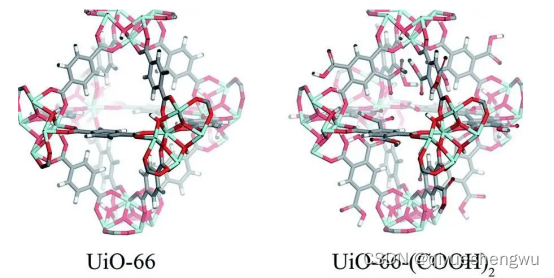
UiO-66-COOH装载苯达莫司汀|羟基磷灰石( HA) 包裹MIL-53(Fe)纳米粒子|装载黄芩苷锰基金属有机骨架材料
3D vision - 2 Introduction to pose estimation - openpose includes installation, compilation and use (single frame, real-time video)
Page generation QR code
![[bw16 application] instructions for firmware burning of Anxin Ke bw16 module and development board update](/img/b8/31609303fd817c48b6fff7c43f31e5.png)
[bw16 application] instructions for firmware burning of Anxin Ke bw16 module and development board update
Go language web development series 27: Gin framework: using gin swagger to implement interface documents
随机推荐
jvm-运行时数据区
[understanding by chance-37]: the structure of human sensory system determines that human beings are self-centered
Qt学习20 Qt 中的标准对话框(中)
Richview trvstyle liststyle list style (bullet number)
Redis:Redis的数据结构、key的操作命令
Using registered classes to realize specific type matching function template
[Jilin University] information sharing of postgraduate entrance examination and re examination
Too many files with unapproved license
GoLand 2021.1: rename the go project
玖逸云黑免费无加密版本源码
Duet date picker (time plug-in that can manually enter the date)
Spring cup eight school league
Formation of mil-100 (FE) coated small molecule aspirin [email protected] (FE) | glycyrrhetinic acid modified metal organ
Dynamic programming 01 knapsack and complete knapsack
FPGA测试方法以Mentor工具为例
Why are grass-roots colleges and universities with "soil and poverty" called "Northeast small Tsinghua"?
Uio-66-cooh loaded bendamostine | hydroxyapatite (HA) coated MIL-53 (FE) nanoparticles | baicalin loaded manganese based metal organic skeleton material
Article content typesetting and code highlighting
Back to top implementation
selenium 浏览器(1)