当前位置:网站首页>关于lg(n!)的渐进紧确界
关于lg(n!)的渐进紧确界
2022-06-21 20:39:00 【ash062】

假设n为2的幂,且 
缩小等式 
记 
进一步处理有 
因此 
类似放大等式 
记 
有 
因此 
综上 
边栏推荐
- Leetcode question brushing: SF Technology Smart logistics Campus Technology Challenge
- An example of CPU instruction rearrangement leading to errors
- 分别利用for、while、do while,循环求1-100的和
- [deeply understand tcapulusdb technology] table management of document acceptance
- Self made C compiler
- Pal2nal| how to run pal2nal from the command line
- [in depth understanding of tcapulusdb technology] tcapulusdb construction data
- IP-guard打印管控,防止打印渠道信息泄露
- 刷题笔记(十六)--二叉树:修改与构造
- [deeply understand tcapulusdb technology] tcapulusdb import data
猜你喜欢
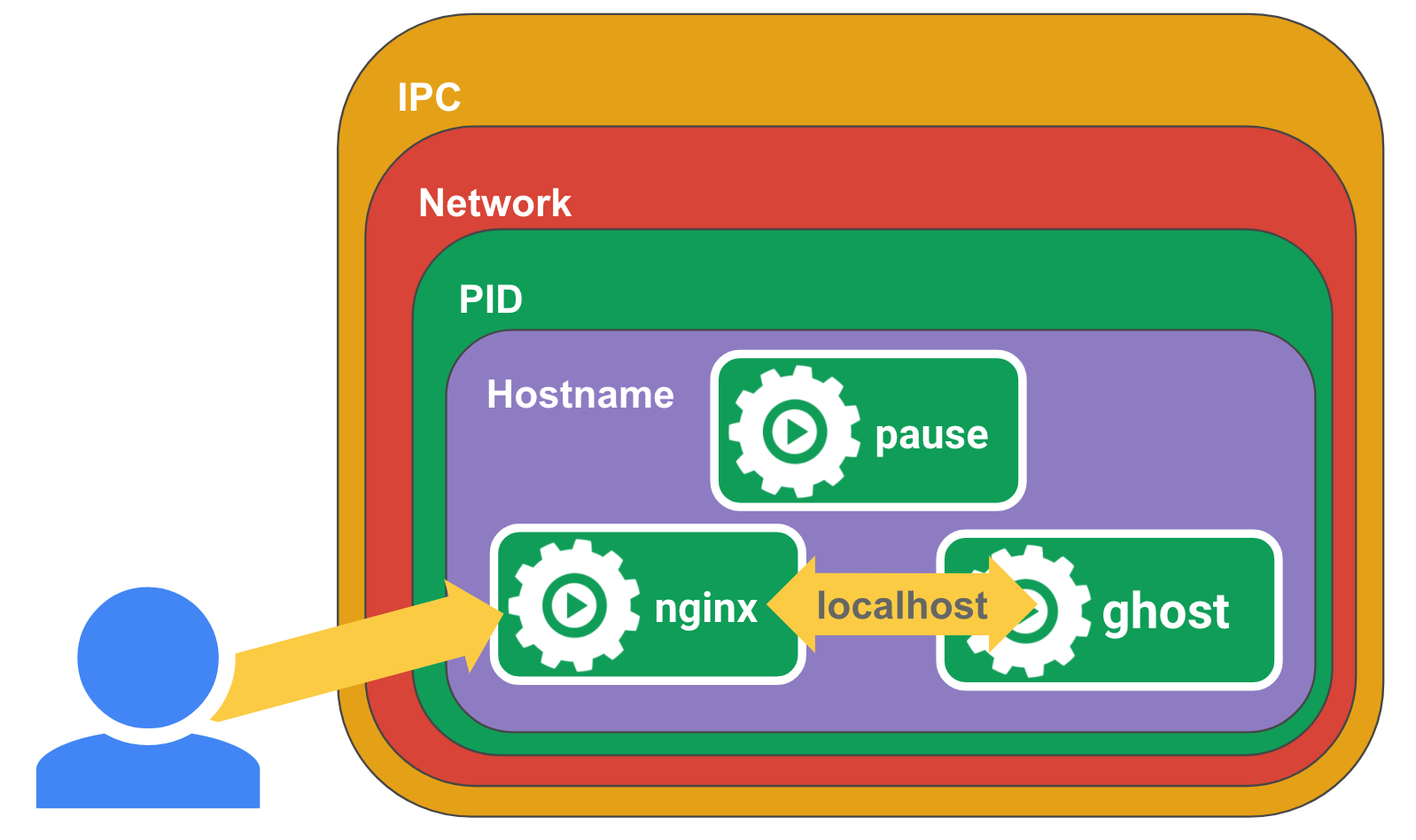
技术分享 | kubernetes pod 简介
![[deeply understand tcapulusdb technology] transaction execution of document acceptance](/img/7c/25a88f46e02cebd2e003b9590b9c13.png)
[deeply understand tcapulusdb technology] transaction execution of document acceptance

五分钟带你了解云原生

Nacos安装指南

MitoZ|Multi-Kmer mode

【深入理解TcaplusDB技术】如何实现Tmonitor单机安装

【深入理解TcaplusDB技术】单据受理之表管理
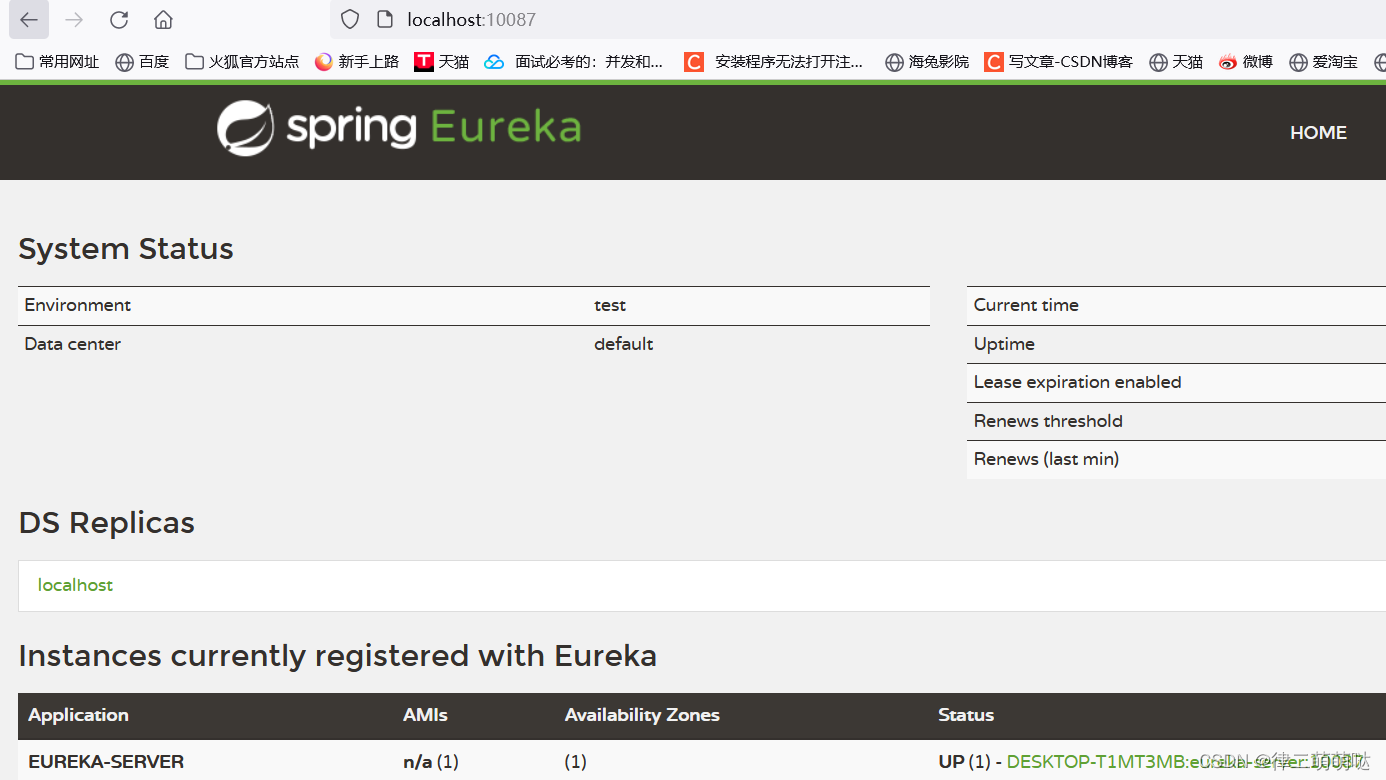
关于eureka启动成功但是访问404问题

PAML|计算dN/dS值的生信软件

Dragon lizard community established cloud native SIG and introduced three core technologies
随机推荐
【深入理解TcaplusDB技术】单据受理之事务执行
企业微信内置应用h5开发记录-1
flutter系列之:flutter中的IndexedStack
Use the for loop to calculate the odd and even sums in 1-100 [method 2]
Mafft|multi sequence alignment tool
Technology sharing | mysql:caching_ sha2_ Password quick Q & A
Jeu de boutons de force 4 (version MySQL)
Technology sharing | a clustering incremental statistical SQL requirement in MySQL
Utilisation de la combinaison d'assertions de l'API Stream et de la mise en cache locale pour les requêtes floues (près de 1000 fois plus efficace que MySQL)
mafft|多序列比对工具
Pi4j GPIO pin pull-up resistance, pull-down resistance concept
安超云入选《CIOReview》2022年亚太区“十大云计算解决方案提供商”
技术分享 | kubernetes pod 简介
Anaconda add channels
【深入理解TcaplusDB技术】Tmonitor后台一键安装
GDB调试实战(8)给程序传递启动参数
leetcode刷题:顺丰科技智慧物流校园技术挑战赛
类库、框架、模块、组件等概念介绍
精彩回顾丨一图了解华为云专场干货
IP-guard打印管控,防止打印渠道信息泄露