Bayesian inference problem, MCMC and variational inference

The Bayesian inference problem

What is Bayesian inference?

• Simply speaking , Bayesian reasoning It is statistical reasoning based on Bayesian paradigm . The basic idea of Bayesian paradigm is to use Bayes theorem To express posterior knowledge $p(\theta |x)$ (the “posterior”)、 Prior knowledge $p(\theta )$ (the “prior”) And likelihood $p(x|\theta )$ (the “likelihood”) The relationship between
  

Computational difficulties

• In many scenarios ,prior and likelihood It's all known , but Normalization factor evidence But you need to integrate to get ：
  The above integral will become difficult to solve in the high-dimensional case , So you need to use some Approximate method To estimate the posterior probability
• Common approximation methods are Markov Chain Monte Carlo and Variational Inference (one should keep in mind that these methods can also be precious when facing other computational difficulties related to Bayesian inference)

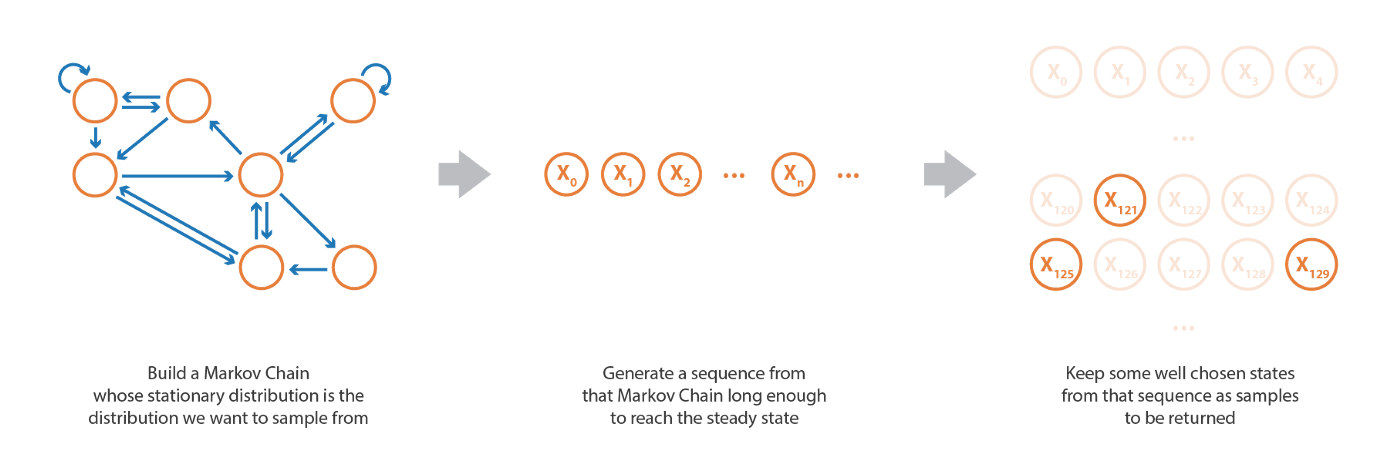
Markov Chains Monte Carlo (MCMC) – A sampling based approach

• Markov chain Monte Carlo method (Markov Chain Monte Carlo, MCMC) (MCMC Whether the probability distribution to be sampled is normalized is not sensitive , It can be sampled even without normalization )
  

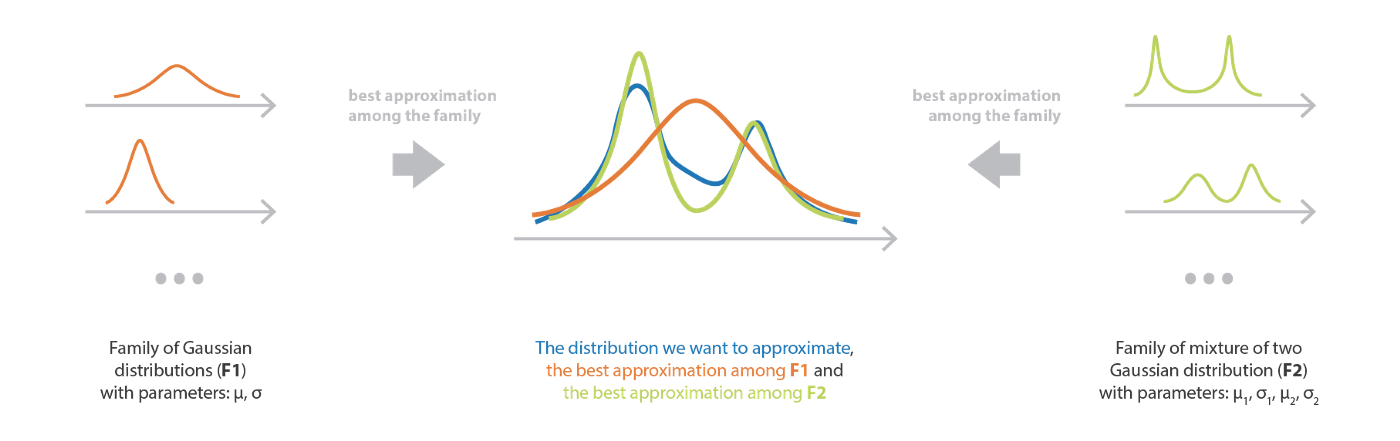
Variational Inference (VI) – An approximation based approach

The approximation approach

• And MCMC Sampling based on Markov chain is different , Variational reasoning Aimed at The best approximate probability distribution of the complex probability distribution to be sampled is found from the specified probability distribution family , In fact, it is to solve an optimization problem
• To be specific , First you need to define a Parameterized probability distribution family , The different probability distributions are determined by the corresponding parameters (e.g. The normal distribution consists of $\mu$ and $\sigma$ control )
  Then you need to start from $F_{\Omega }$ Find a probability distribution closest to the probability distribution to be sampled ${\omega }^{\ast }$, The solution is as follows Optimization problems ：
  among ,$\pi$ Is the probability distribution to be sampled ,$E(p,q)$ Used to measure the distance between two probability distributions . In variational reasoning ,$E(p,q)$ by KL The divergence , The optimization process adopts gradient descent ( because KL Divergence is right $p$ Normalization insensitive , Therefore, variational reasoning does not require normalization of the probability distribution to be sampled )
  

Family of distribution

• The choice of probability distribution family It is actually a very strong prior information , It determines the approximate probability distribution to be sampled bias And the optimization process Complexity . If the distribution family is too simple , So similar bias It will be very big , But the optimization process is simple , conversely bias It will be smaller , But the optimization process is more complicated . therefore , We need to maintain bias And complexity
  

---

Mean field variation family (mean-field variational family)

• In the mean field variational family , All components of a random vector are independent , therefore Probability density function It can be written in the following formula ：
  among ,$z$ by $m$ A random vector of dimensions ,$f_j$ by $z$ Of the $j$ Probability density function of components

Kullback-Leibler divergence

• When looking for the approximate distribution of the probability distribution to be sampled , We hope that the optimization process is insensitive to the normalization factor , While using KL Divergence as a measure can well meet this condition . set up $\pi$ Is the probability distribution to be sampled ,$C$ Is the normalization factor
  be
  therefore In the use of KL Divergence as a measure , The optimization process is insensitive to the normalization factor , We do not need to normalize the sampling probability ：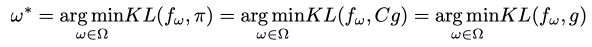
  

Optimisation process and intuition

• The above optimization problem can be solved by gradient descent And other methods to find the optimal solution

---

Intuition

• To better understand the above optimization process , The following is an example of Bayesian inference ：
  As you can see from the last item , The best approximate a posteriori probability distribution will make based on the observed data $x$ Of The log likelihood is expected to be as large as possible , At the same time, the approximate posterior distribution And a priori distribution KL The divergence should be as small as possible (prior/likelihood balance)

MCMC v.s. VI

• MCMC and VI There are different applications . One side ,MCMC Sampling process Large amount of calculation but bias smaller , Therefore, it is suitable for situations that need to get accurate results without caring about the time cost . On the other hand ,VI The selection and optimization process of the probability distribution family in bias, comparison MCMC for bias more but Less computational overhead , Therefore, it is suitable for large-scale reasoning problems that need fast computation

References

• Bayesian inference problem, MCMC and variational inference
• more about VI: Variational Inference: A Review for Statisticians
• more about MCMC: Introduction to Markov Chain Monte Carlo、An Introduction to MCMC for Machine Learning
• more about Gibbs Sampling applied to LDA: Tutorial on Topic Modelling and Gibbs Sampling、lecture note on LDA Gibbs Sampler