当前位置：网站首页>【数学】【连续介质力学】流体力学中的对称张量、应变张量和应力张量

【数学】【连续介质力学】流体力学中的对称张量、应变张量和应力张量

2022-06-10 22:31:00 【beidou111】

文章目录

问题的由来
速度梯度
对称张量
应变张量
应力张量

问题的由来

在splishsplash论文教程当中，在讲到粘性的时候，有这样一页PPT
在这里插入图片描述
这是流体力学的基础知识，即利用牛顿本构模型来构建的NS方程。

我们先看左边这个公式

在这里插入图片描述
被称为柯西动量方程。这个方程对流体力学和固体力学全都适用。因此可以视为NS方程更基础的存在。它其实就是一个线动量方程。左边的加速度，右边是内力（由应力表示，为面力）和外力（一般是体力）。

其中T是应力张量。

我们再看右边这个公式。

在这里插入图片描述
这个公式就是牛顿本构方程。针对于牛顿流体所构建出来的方程。如果不是牛顿流体，就不适用。所谓的本构方程，就是找到应力与应变的关系。实际上，按照固体力学的说法，第二个方程是一个几何方程。第一个方程是物理方程，或者叫本构方程。我们这里暂且不区分，都叫他本构方程。

但是，我们的重点并不在于方程本身。我们的目的是让读者熟悉这些数学记号的含义。也就是说，我们从张量数学的角度来看看这些量写成我们熟悉的矩阵形式是什么样的？

其他的都没有什么难度。唯一我们不熟悉的就是速度梯度了。即
$\nabla \mathbf{v}$

我们之前写过一篇关于张量的通俗入门，如下：
https://blog.csdn.net/weixin_43940314/article/details/123559800

速度梯度

速度显然是个向量
$\mathbf{v} = (u, v, w)^T$

而nabla算子也只是个向量
$\nabla = (\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z})^T$

向量与向量写到一块，中间没有任何符号，实际上是并乘（也叫并矢）。有时候我们也主动的添加一个符号，写成 $\bigotimes$ 。

其实，梯度就是nabla算子与物理量的并乘。

并乘遵循什么规则呢？

并乘和点乘、叉乘不同，它什么也不做！只是单纯的把矢量并排着写在一起。

此外，记住：并乘是升阶的，结果的阶数就是把原来的阶数加起来！

下面我们把并乘写成熟悉的矩阵形式。

我们一行一行地写
$\nabla \otimes \mathbf{v} = \begin{pmatrix} \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y}\\ \frac{\partial}{\partial z} \end{pmatrix} \otimes \begin{pmatrix} u \\ v\\ w \end{pmatrix}$

1 第一行

对应的项简单地并排写在一起

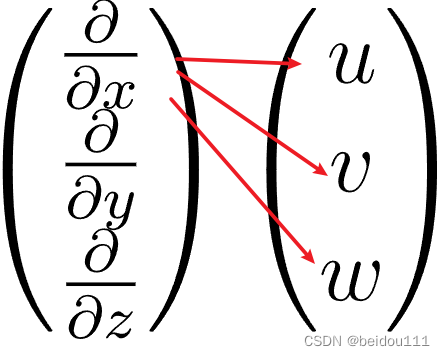
在这里插入图片描述

1.1 分量和形式

写成分量和的形式
$\frac{\partial u}{\partial x} \mathbf{ii} + \frac{\partial v}{\partial x }\mathbf{ij} + \frac{\partial w}{\partial x} \mathbf{ik}$

1.2 矩阵形式

或者写成矩阵的形式

也就是

$\begin{pmatrix} \frac{\partial u}{\partial x} & \frac{\partial v}{\partial x } & \frac{\partial w}{\partial x} \\ \cdots & \cdots & \cdots\\ \cdots & \cdots & \cdots\\ \end{pmatrix}$

2 第二行

同理

在这里插入图片描述

2.1 分量和形式

写成分量和的形式
$\frac{\partial u}{\partial y} \mathbf{ii} + \frac{\partial v}{\partial y }\mathbf{ij} + \frac{\partial w}{\partial y} \mathbf{ik}$

2.2 矩阵形式

或者写成矩阵的形式

也就是

$\begin{pmatrix} \cdots & \cdots & \cdots\\ \frac{\partial u}{\partial y} & \frac{\partial v}{\partial y} & \frac{\partial w}{\partial y}\\ \cdots & \cdots & \cdots\\ \end{pmatrix}$

3 第三行

同理
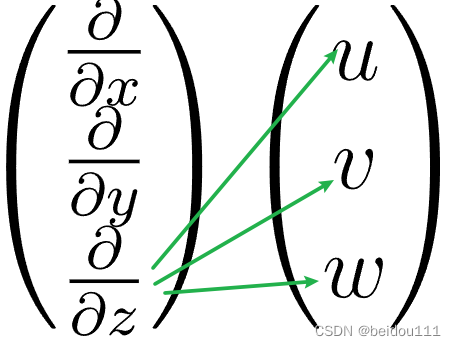
在这里插入图片描述

3.1 分量和形式

写成分量和的形式
$\frac{\partial u}{\partial z} \mathbf{ii} + \frac{\partial v}{\partial z }\mathbf{ij} + \frac{\partial w}{\partial z} \mathbf{ik}$

3.2 矩阵形式

或者写成矩阵的形式

也就是

$\begin{pmatrix} \cdots & \cdots & \cdots\\ \cdots & \cdots & \cdots\\ \frac{\partial u}{\partial z} & \frac{\partial v}{\partial z} & \frac{\partial w}{\partial z}\\ \end{pmatrix}$

4 合在一起

在这里插入图片描述
分量和形式
$\nabla \mathbf{v} = \\ \frac{\partial u}{\partial x} \mathbf{ii} + \frac{\partial v}{\partial x }\mathbf{ij} + \frac{\partial w}{\partial x} \mathbf{ik} + \\ \frac{\partial u}{\partial y} \mathbf{ii} + \frac{\partial v}{\partial y }\mathbf{ij} + \frac{\partial w}{\partial y} \mathbf{ik} + \\ \frac{\partial u}{\partial z} \mathbf{ii} + \frac{\partial v}{\partial z }\mathbf{ij} + \frac{\partial w}{\partial z} \mathbf{ik}$

矩阵形式

对称张量

我们写出了速度梯度，现在来看一下对称张量
$\nabla \mathbf{v} + (\nabla \mathbf{v})^T$

不过就是速度梯度加上它自己的转置而已。

转置就是行写成列，列写成行。

我们先写出转置
$(\nabla \mathbf{v})^T= \begin{pmatrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y } & \frac{\partial u}{\partial z} \\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} & \frac{\partial v}{\partial z}\\ \frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} & \frac{\partial w}{\partial z}\\ \end{pmatrix}$

然后再把它们加起来

$\begin{pmatrix} \frac{\partial u}{\partial x} & \frac{\partial v}{\partial x } & \frac{\partial w}{\partial x} \\ \frac{\partial u}{\partial y} & \frac{\partial v}{\partial y} & \frac{\partial w}{\partial y}\\ \frac{\partial u}{\partial z} & \frac{\partial v}{\partial z} & \frac{\partial w}{\partial z}\\ \end{pmatrix} + \begin{pmatrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y } & \frac{\partial u}{\partial z} \\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} & \frac{\partial v}{\partial z}\\ \frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} & \frac{\partial w}{\partial z}\\ \end{pmatrix} =\\ \begin{pmatrix} 2\frac{\partial u}{\partial x} &\frac{\partial v}{\partial x }+\frac{\partial u}{\partial y } & \frac{\partial w}{\partial x}+\frac{\partial u}{\partial z} \\ \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} & 2\frac{\partial v}{\partial y} & \frac{\partial w}{\partial y}+\frac{\partial v}{\partial z}\\ \frac{\partial u}{\partial z}+\frac{\partial w}{\partial x} & \frac{\partial v}{\partial z}+\frac{\partial w}{\partial y} & 2 \frac{\partial w}{\partial z}\\ \end{pmatrix}$

我们观察这个矩阵
$\nabla \mathbf{v} + (\nabla \mathbf{v})^T= \begin{pmatrix} 2\frac{\partial u}{\partial x} &\frac{\partial v}{\partial x }+\frac{\partial u}{\partial y } & \frac{\partial w}{\partial x}+\frac{\partial u}{\partial z} \\ \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} & 2\frac{\partial v}{\partial y} & \frac{\partial w}{\partial y}+\frac{\partial v}{\partial z}\\ \frac{\partial u}{\partial z}+\frac{\partial w}{\partial x} & \frac{\partial v}{\partial z}+\frac{\partial w}{\partial y} & 2 \frac{\partial w}{\partial z}\\ \end{pmatrix}$

可以很容易的发现两个特点：

它是对称的
对角线元素有个系数2

实际上，任何矩阵加上它的转置都是对称的。这点很容易就能想通。

所以，在流体力学中，我们就管它叫对称张量好了。（狂野但简单粗暴的名字）

顺带一提，在OpenFOAM当中，它的代码表示就是

twoSymm(gradU)

为啥加个two呢？因为它是2倍的应变张量。我们其实可以这样记忆：它对角元有个系数2。

应变张量

刚才说了，应变张量其实就是1/2的对称张量。

$\frac{1}{2}(\nabla \mathbf{v} + (\nabla \mathbf{v})^T)$

简单明了。

应力张量

到上面为止，我们都没用到牛顿本构。也就是说，上面的内容对任何流体都是适用的。

这时候再套入牛顿本构方程。

假如为牛顿流体
$\mathbf{T}=-p \mathbb{1}+2 \mu \mathbf{E}$
这里的1是单位阵。

所以无非就是乘以了几个系数。

$\mathbf{T}=-p \mathbb{1}+2 \mu \mathbf{E}=\\ \begin{pmatrix} 2\mu \frac{\partial u}{\partial x} -p & \mu ( \frac{\partial v}{\partial x }+\frac{\partial u}{\partial y }) & \mu ( \frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}) \\ \mu ( \frac{\partial u}{\partial y}+ \frac{\partial v}{\partial x}) & 2\mu \frac{\partial v}{\partial y}-p & \mu ( \frac{\partial w}{\partial y}+\frac{\partial v}{\partial z})\\ \mu ( \frac{\partial u}{\partial z}+ \frac{\partial w}{\partial x}) & \mu ( \frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}) & 2\mu \frac{\partial w}{\partial z}-p\\ \end{pmatrix}$