数电快速入门（二）（复合逻辑运算和逻辑代数的基本定律的介绍）

回顾：这本系列（一）中，我们讲到了BCD码和三个最基本的逻辑运算。

1.4.2 复合逻辑运算

1：‘与非’逻辑

一般定义：是‘与’逻辑和‘非’逻辑的结合，两者顺序是先‘与’后‘非’（在逻辑函数表达式中可以体现）。

‘与非’逻辑函数式为（A、B为条件）：

‘与非’逻辑的真值表：

A	B
0	0	1
0	1	1
1	0	1
1	1	0

 ‘与非’逻辑的逻辑功能概括：

有0出1，全1出0(从真值表中可以看出A和B无论哪个是0，其F=1；只有当A和B都等于1时，F=0)

2：‘异或’逻辑

‘异或’逻辑函数式为（A、B为条件）：

‘异或’逻辑的真值表：

A	B
0	0	0
0	1	1
1	0	1
1	1	0

  ‘异或’逻辑的逻辑功能概括：

相异出1，相同出0（从真值表中可以看出当A和B两者不同时，F=1；反之F=0）

3：‘同或’逻辑

‘同或’逻辑函数式为（A、B为条件）：

‘同或’逻辑的真值表：

A	B
0	0	1
0	1	0
1	0	0
1	1	1

‘同或’逻辑的逻辑功能概括：

相异出0，相同出1（从真值表中可以看出当A和B两者不同时，F=0；反之F=1）

部分逻辑门电路符号如下图所示：

 注：同或门的符号就是把异或门中的‘=1’改成‘=’就行。

1.5 逻辑代数的基本定律（重要）

注：以下的*均为点乘！！！！

且下文所说的相与和相或分别是相点乘和相加，这可以从前面系列（一）中的与和或中的逻辑函数表达式可以看出。

1:0-1律（A表示条件）

A*0=0（这里表示，无论A=1还是0，当A和0相与时，结果都是0）；

A+1=1（这里表示，无论A=1还是0，当A和1相或时，结果都是1）

2：自等律（A表示条件）

A*1=A（这里表示，无论A=1还是0，当A和1相与时，结果都是1）；

A+0=A（这里表示，无论A=1还是0，当A和0相或时，结果都是A本身）

3：重叠律（A表示条件）

A*A=A（这里表示，无论A=1还是0，当A与A相与时，结果都是A本身）

A+A=A（这里表示，无论A=1还是0，当A和A相或时，结果都是A本身）

4：互补律（A表示条件）

（这里表示，无论A=1还是0，当A与A非相与时，结果都是0）

（这里表示，无论A=1还是0，当A与A非相或时，结果都是1）

5：交换律、结合律、分配率

因为与普通代数计算格式相同，这里不过多赘述。

6：反演律（重要）（A、B为条件）

（这里表示，无论A和B等于1还是0，当A与B相或非时，结果是A非与B非）

（这里表示，无论A和B等于1还是0，当A与B相与非时，结果是A非或B非）

7：还原律（A为条件）

1.6 逻辑函数的标准形式

1：最小项

定义：最小项是一种特殊的乘积项（是一种‘与’项，例如：等只有乘积项，没有相加项）

特点：

（1）n变量的逻辑函数的最小项，一定包含n个因子（例如，有ABC三个变量的逻辑函数，每一个最小项都会存在这三种逻辑变量）

（2）在各个最小项中，每个变量以原变量或者反变量的形式作为因子仅出现一次（在ABC三个变量的逻辑函数中，A、B、C这三个原变量或者、、这三个反变量在一个最小项中只能出现一次，如：ABC、这些是正确的最小项）

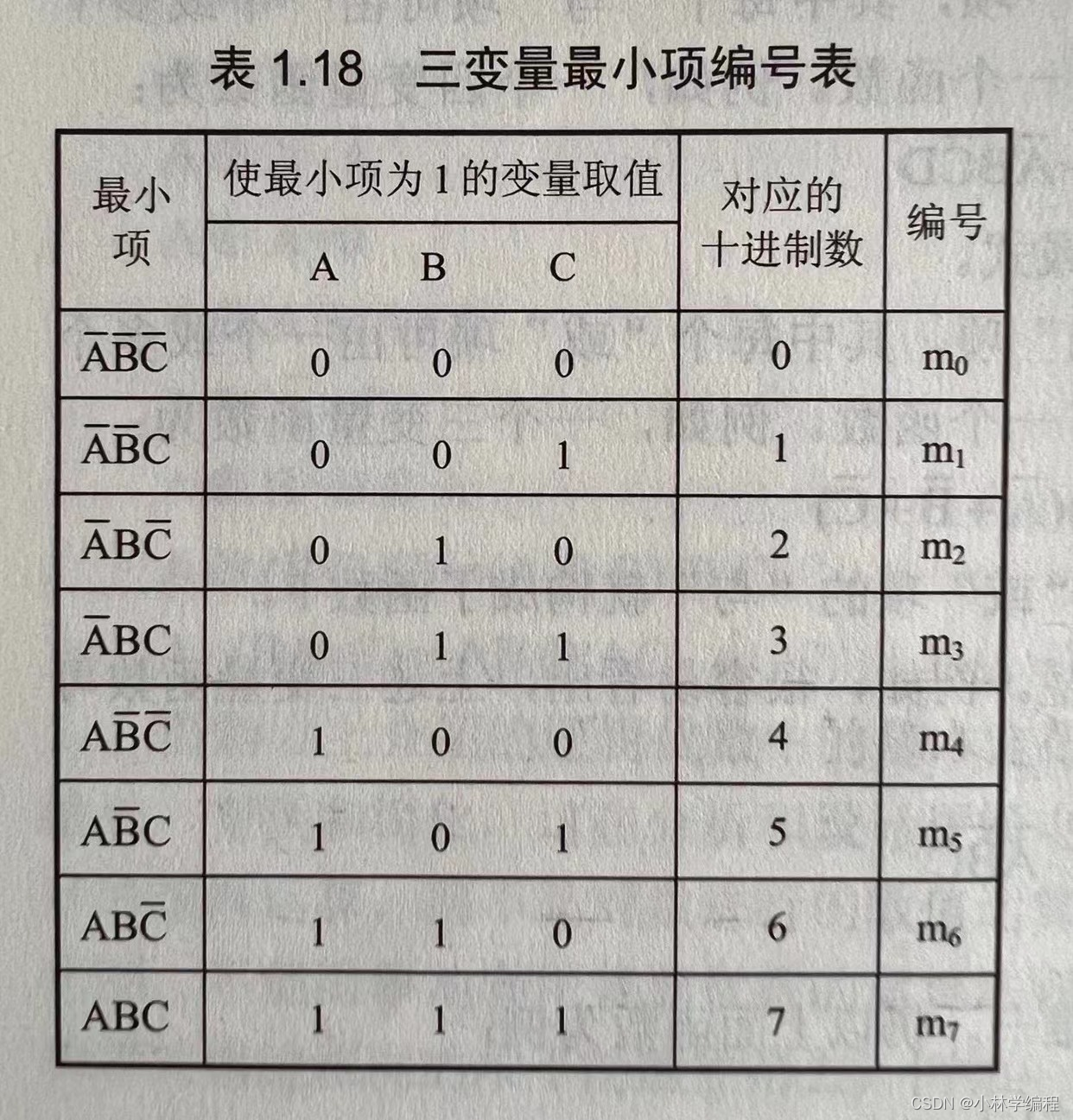
为了方便书写，对最小项进行编号,m表示最小项，i是代号，例如的代号为101（如果是原变量则表示为1，反变量表示为0），则i=5（用二进制来计算）

如下图所示：

 若两个最小项中一个带原变量另一个带该原变量的反变量，则该变量可以被消去，例如：。

2：标准与或式

标准与或式的逻辑函数是积之和形式（与或式），而且其中每一个乘积项（与项）都是最小项。

比如,为每个最小项，就是一种标准与或式。