当前位置:网站首页>【刷题篇】二叉树的右视图
【刷题篇】二叉树的右视图
2022-08-03 21:33:00 【m0_60631323】
一、题目
OJ链接
请根据二叉树的前序遍历,中序遍历恢复二叉树,并打印出二叉树的右视图
示例: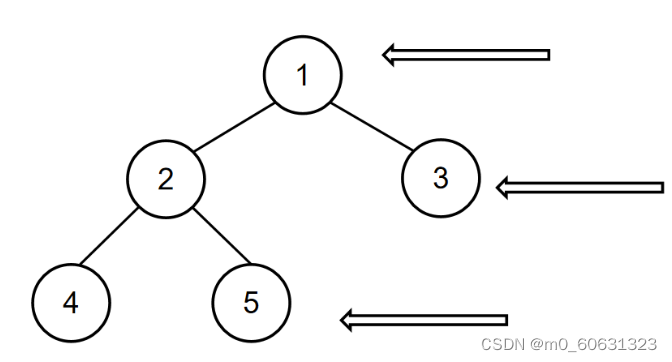
对应的输出为[1,3,5]。
二、题解
解决本题主要 分两个步骤:
- 根据前序和中序构建出二叉树
- 对二叉树进行层次遍历,找到每一层的最右侧的节点
构建二叉树:
参考链接: 二叉树相关OJ题
中序遍历找出最每一层最右侧的节点:
层序遍历的过程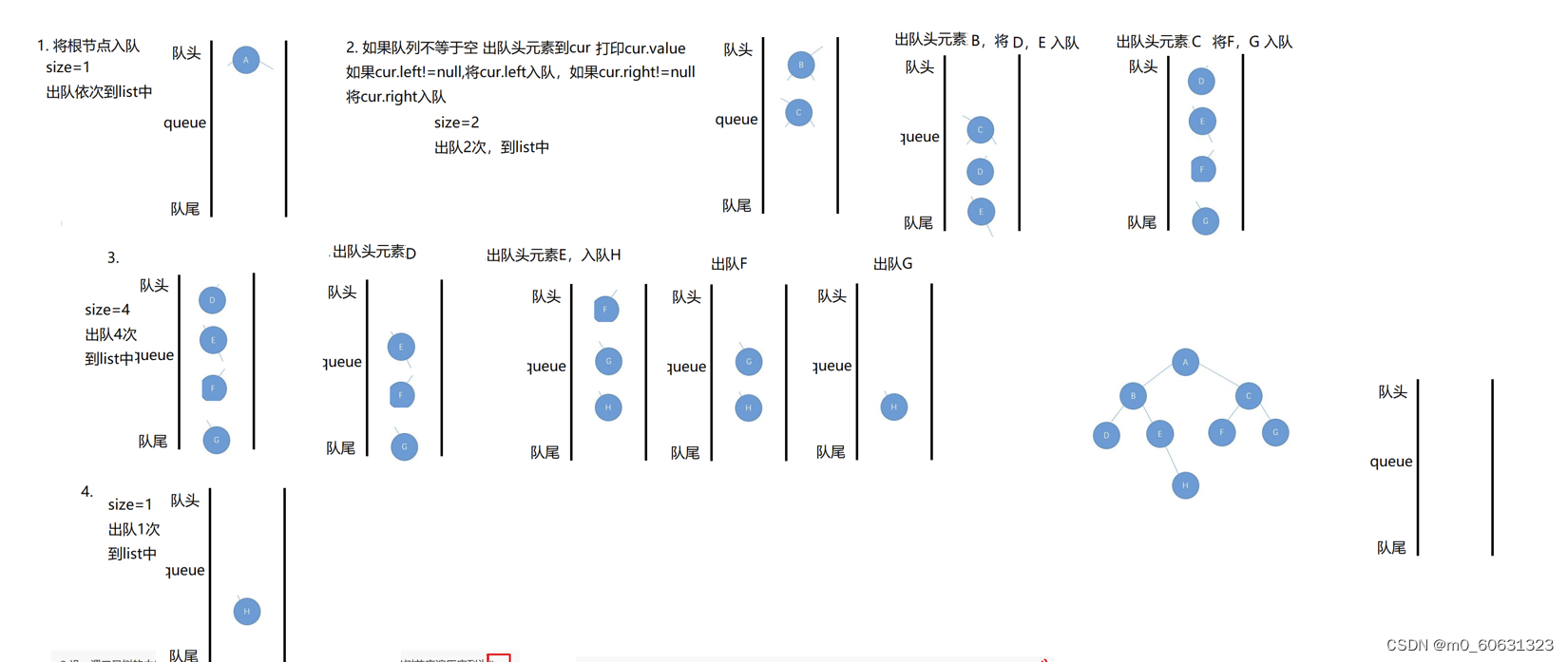
变量size记录的是当前遍历到的层的节点数,我们在入队的时候的顺序是:从左到右依次将当前层的节点加入到队列中,所以在出队的时候,当前层的最右侧的节点一定是该层所有节点中最后一个出队列的
故我们可根据这一特点,增设一个判断条件,但size为0时,此时上一次出的元素就是当前层的最右侧的元素
源码:
public class Solution {
/** * 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可 * 求二叉树的右视图 * @param xianxu int整型一维数组 先序遍历 * @param zhongxu int整型一维数组 中序遍历 * @return int整型一维数组 */
int preIndex=0;
HashMap<Integer,Integer> map=new HashMap<>();
public void RootIndex(int[] inorder){
for (int i = 0; i < inorder.length; i++) {
map.put(inorder[i],i);
}
}
public ArrayList<Integer> rightSideView(TreeNode root) {
ArrayList<Integer> res = new ArrayList<Integer>();
Queue<TreeNode> q = new LinkedList<TreeNode>();
q.offer(root);
while(!q.isEmpty()){
//队列中的大小即是这一层的节点树
int size = q.size();
while(size-- != 0){
TreeNode temp = q.poll();
if(temp.left != null)
q.offer(temp.left);
if(temp.right != null)
q.offer(temp.right);
//最右元素
if(size == 0)
res.add(temp.val);
}
}
return res;
}
public int[] solve (int[] xianxu, int[] zhongxu) {
TreeNode root=buildTree(xianxu,zhongxu);
ArrayList<Integer> tmp=rightSideView(root);
int[] arr=new int[tmp.size()];
for(int i=0;i<tmp.size();i++){
arr[i]=tmp.get(i);
}
return arr;
}
public TreeNode buildTree(int[] xianxu,int[] zhongxu ){
RootIndex(zhongxu);
return buildTreeChild(xianxu,zhongxu,0,zhongxu.length-1);
}
public TreeNode buildTreeChild(int[] xianxu,int[] zhongxu,int inbegin,int inend){
if(inbegin>inend){
return null;
}
TreeNode root=new TreeNode(xianxu[preIndex]);
int ri=map.get(xianxu[preIndex]);
preIndex++;
root.left=buildTreeChild(xianxu,zhongxu,inbegin,ri-1);
root.right=buildTreeChild(xianxu,zhongxu,ri+1,inend);
return root;
}
}
边栏推荐
- C. Array Elimination-- Codeforces Round #751 (Div. 2)
- Diazo Biotin-PEG3-DBCO|重氮化合物修饰生物素-三聚乙二醇-二苯并环辛炔
- 《富爸爸,穷爸爸》思维导图和学习笔记
- 图神经网络怎么入门?一文带你了解图神经网络入门路径-GNN入门
- 测试2年6.5K,每天“911”,我的心酸经历只有我自己知道···
- 【使用 Pytorch 实现入门级的人工神经网络】
- 关于GPIO你真的懂了吗?这篇文章都给你整理好了
- idea2021配置svn报错Cannot run program “svn“ (in directory “xxx“):CreateProcess error=2,系统找不到指定的文件
- 安全基础8 ---XSS
- 6. XML
猜你喜欢
![[kali-vulnerability scanning] (2.1) Nessus lifts IP restrictions, scans quickly without results, and plugins are deleted (middle)](/img/93/0b78b6a930380aeecfbbb156df7498.png)
[kali-vulnerability scanning] (2.1) Nessus lifts IP restrictions, scans quickly without results, and plugins are deleted (middle)
XSS online shooting range---prompt
tidyverse based on data.table?
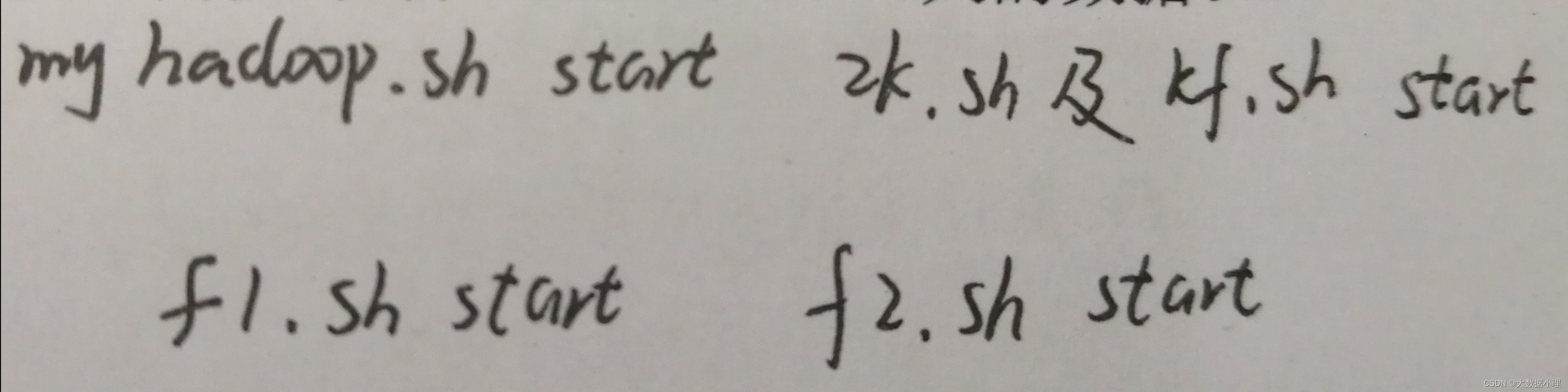
E-commerce data warehouse ODS layer-----log data loading

安全基础8 ---XSS
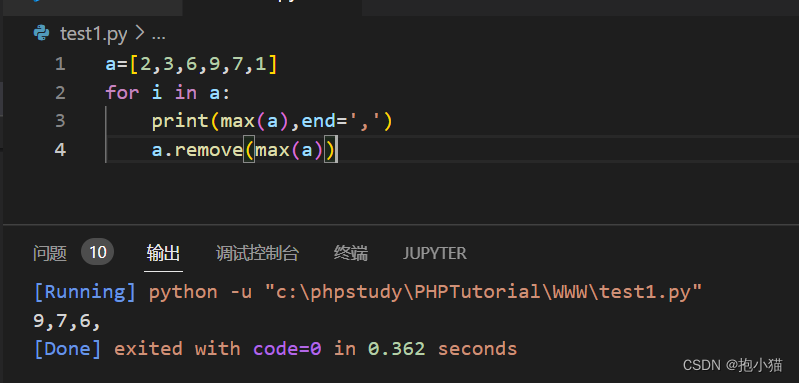
XSS练习---一次循环和两次循环问题
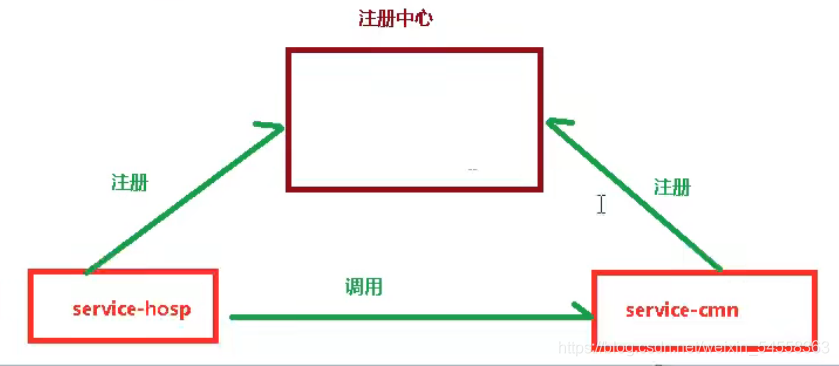
尚医通项目总结

XSS测试

距LiveVideoStackCon 2022 上海站开幕还有3天!
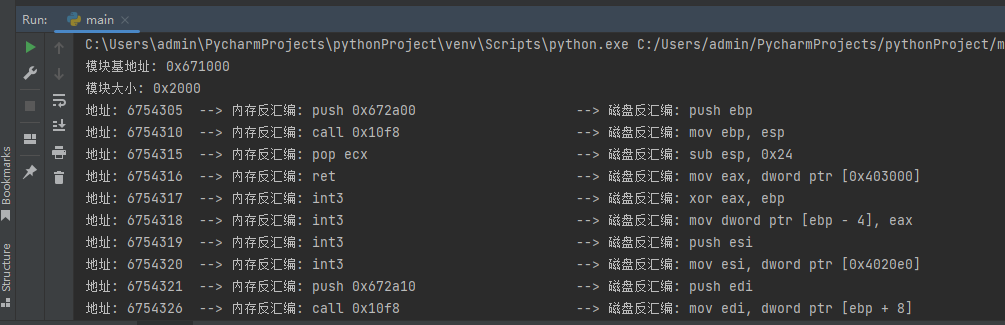
LyScript 实现应用层钩子扫描器
随机推荐
从开发到软件测试:除了扎实的测试基础,还有哪些必须掌握 ?
函数,递归以及dom简单操作
关于GPIO你真的懂了吗?这篇文章都给你整理好了
Orcad Capture Cadence 新建原理图多部分smybol和Homogeneous、Heterogeneous类型介绍教程
【kali-漏洞扫描】(2.1)Nessus下载安装(上)
小朋友学C语言(3):整数、浮点数、字符
IO线程进程->线程同步互斥机制->day6
4. 模块化编程
『百日百题 · 基础篇』备战面试,坚持刷题 第四话——循环语句!
A. Color the Picture- Codeforces Round #810 (Div. 1)
2022年全国职业院校技能大赛网络安全 B模块 任务十windows操作系统渗透测试 国赛原题
6. XML
肝完 Alibaba 这份面试通关宝典,我成功拿下今年第 15 个 Offer
nxp官方uboot移植到野火开发板PRO(修改LCD部分和网络部分)
XSS practice - cycle and two cycle problem at a time
CAS:1260586-88-6_Biotin-C5-Azide_Biotin-C5-Azide
2021年数据泄露成本报告解读
nxp官方uboot移植到野火开发板PRO(无任何代码逻辑的修改)
376. Wiggle Subsequence
深度学习怎么入门?零基础快速入门深度学习