当前位置:网站首页>[combinatorics] generating function (summation property)
[combinatorics] generating function (summation property)
2022-07-03 17:46:00 【Programmer community】
List of articles
- One 、 Summation property of generating function 1 ( Sum forward )
- Two 、 Summation property of generating function 2 ( Backward summation )
Reference blog :
- 【 Combinatorial mathematics 】 Generating function Brief introduction ( Generating function definition | Newton's binomial coefficient | Common generating functions | Related to constants | Related to binomial coefficient | Related to polynomial coefficients )
- 【 Combinatorial mathematics 】 Generating function ( Linear properties | Product properties )
- 【 Combinatorial mathematics 】 Generating function ( Shift property )
One 、 Summation property of generating function 1 ( Sum forward )
Summation property of generating function 1 :
b
n
=
∑
i
=
0
n
a
i
b_n = \sum\limits_{i=0}^{n}a_i
bn=i=0∑nai , be
B
(
x
)
=
A
(
x
)
1
−
x
B(x) = \cfrac{A(x)}{1-x}
B(x)=1−xA(x)
The sequence
a
n
a_n
an The generating function of is
A
(
x
)
A(x)
A(x) , The sequence
b
n
b_n
bn The generating function of is
B
(
x
)
B(x)
B(x) ,
The sequence
a
n
=
{
a
0
,
a
1
,
a
2
,
⋯
}
a_n = \{ a_0 , a_1, a_2 , \cdots \}
an={ a0,a1,a2,⋯} , The sequence
b
n
=
{
b
0
,
b
1
,
b
2
,
⋯
}
b_n = \{ b_0 , b_1, b_2 , \cdots \}
bn={ b0,b1,b2,⋯} ;
The sequence
a
n
a_n
an The generating function of
A
(
x
)
=
a
0
+
a
1
x
+
a
2
x
2
+
⋯
A(x) = a_0 + a_1x + a_2x^2 + \cdots
A(x)=a0+a1x+a2x2+⋯
The sequence
b
n
b_n
bn The generating function of
B
(
x
)
=
b
0
+
b
1
x
+
b
2
x
2
+
⋯
B(x) = b_0 + b_1x + b_2x^2 + \cdots
B(x)=b0+b1x+b2x2+⋯
b
n
b_n
bn The second in a series
n
n
n term , be equal to
a
n
a_n
an The first in a sequence
n
n
n Sum of items ;
deduction
b
n
b_n
bn Items of sequence :
b
0
=
a
0
b_0 = a_0
b0=a0
b
1
=
a
0
+
a
1
b_1 = a_0 + a_1
b1=a0+a1
b
2
=
a
0
+
a
1
+
a
2
b_2 = a_0 + a_1 + a_2
b2=a0+a1+a2
⋮
\vdots
⋮
b
n
=
a
0
+
a
1
+
a
2
+
⋯
+
a
n
b_n = a_0 + a_1 + a_2 + \cdots + a_n
bn=a0+a1+a2+⋯+an
Derive the terms of the generating function :
B
(
x
)
B(x)
B(x) Medium
x
0
x^0
x0 term ( Constant term ) :
b
0
=
a
0
b_0 \ \ \ = a_0
b0 =a0
B
(
x
)
B(x)
B(x) Medium
x
1
x^1
x1 term ( Constant term ) :
b
1
x
=
(
a
0
+
a
1
)
x
b_1x \ = (a_0 + a_1)x
b1x =(a0+a1)x
B
(
x
)
B(x)
B(x) Medium
x
2
x^2
x2 term ( Constant term ) :
b
2
x
2
=
(
a
0
+
a
1
+
a
2
)
x
2
b_2x^2 = (a_0 + a_1 + a_2)x^2
b2x2=(a0+a1+a2)x2
⋮
\vdots
⋮
B
(
x
)
B(x)
B(x) Medium
x
n
x^n
xn term ( Constant term ) :
b
n
x
n
=
(
a
0
+
a
1
+
a
2
+
⋯
+
a
n
)
x
n
b_nx^n = (a_0 + a_1 + a_2 + \cdots + a_n)x^n
bnxn=(a0+a1+a2+⋯+an)xn
Put the above
B
(
x
)
B(x)
B(x) Add the items in : The strategy of addition is vertical addition , As shown in the figure below :

The first
1
1
1 Column addition :
a
0
+
a
0
x
+
a
0
x
2
+
⋯
+
a
0
x
n
=
a
0
1
1
−
x
a_0 + a_0 x + a_0x^2 + \cdots + a_0x^n = a_0\cfrac{1}{1-x}
a0+a0x+a0x2+⋯+a0xn=a01−x1
The first
2
2
2 Column addition :
a
1
x
+
a
1
x
2
+
⋯
+
a
1
x
n
=
a
1
x
1
1
−
x
a_1 x + a_1x^2 + \cdots + a_1x^n = a_1x\cfrac{1}{1-x}
a1x+a1x2+⋯+a1xn=a1x1−x1
⋮
\vdots
⋮
The first
n
n
n Column addition :
a
n
x
n
=
a
n
x
n
1
1
−
x
a_nx^n = a_nx^n\cfrac{1}{1-x}
anxn=anxn1−x1
The resulting :
B
(
x
)
=
a
0
1
1
−
x
+
a
1
x
1
1
−
x
+
⋯
+
a
n
x
n
1
1
−
x
+
⋯
B(x) = a_0\cfrac{1}{1-x} + a_1x\cfrac{1}{1-x} + \cdots + a_nx^n\cfrac{1}{1-x} + \cdots
B(x)=a01−x1+a1x1−x1+⋯+anxn1−x1+⋯
Will be one of the
1
1
−
x
\cfrac{1}{1-x}
1−x1 extracted , You can get :
B
(
x
)
=
1
1
−
x
(
a
0
+
a
1
x
+
+
⋯
+
a
n
x
n
+
⋯
)
B(x) = \cfrac{1}{1-x} ( a_0 + a_1x + + \cdots + a_nx^n + \cdots )
B(x)=1−x1(a0+a1x++⋯+anxn+⋯)
B
(
x
)
=
1
1
−
x
A
(
x
)
B(x) = \cfrac{1}{1-x} A(x)
B(x)=1−x1A(x)
Two 、 Summation property of generating function 2 ( Backward summation )
Summation property of generating function 2 :
b
n
=
∑
i
=
n
∞
a
i
b_n = \sum\limits_{i=n}^{\infty}a_i
bn=i=n∑∞ai , also
A
(
1
)
=
∑
i
=
n
∞
a
i
A(1) =\sum\limits_{i=n}^{\infty}a_i
A(1)=i=n∑∞ai convergence , be
B
(
x
)
=
A
(
1
)
−
x
A
(
x
)
1
−
x
B(x) = \cfrac{A(1) - xA(x)}{1-x}
B(x)=1−xA(1)−xA(x)
边栏推荐
- SQL injection database operation foundation
- Research on Swift
- Leetcode540: a single element in an ordered array
- [mathematical logic] equivalent calculus and reasoning calculus of predicate logic (individual word | predicate | quantifier | predicate logic formula | two basic formulas | proposition symbolization
- What is the difference between cloud server and cloud virtual machine
- PHP processing - watermark images (text, etc.)
- 1164 Good in C
- 国内如何购买Google Colab会员
- AcWing 3438. Number system conversion
- VM11289 WAService. js:2 Do not have __ e handler in component:
猜你喜欢

PS screen printing brush 131, many illustrators have followed suit
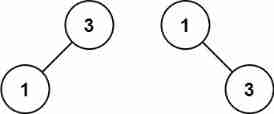
Leetcode 108 converts an ordered array into a binary search tree -- recursive method
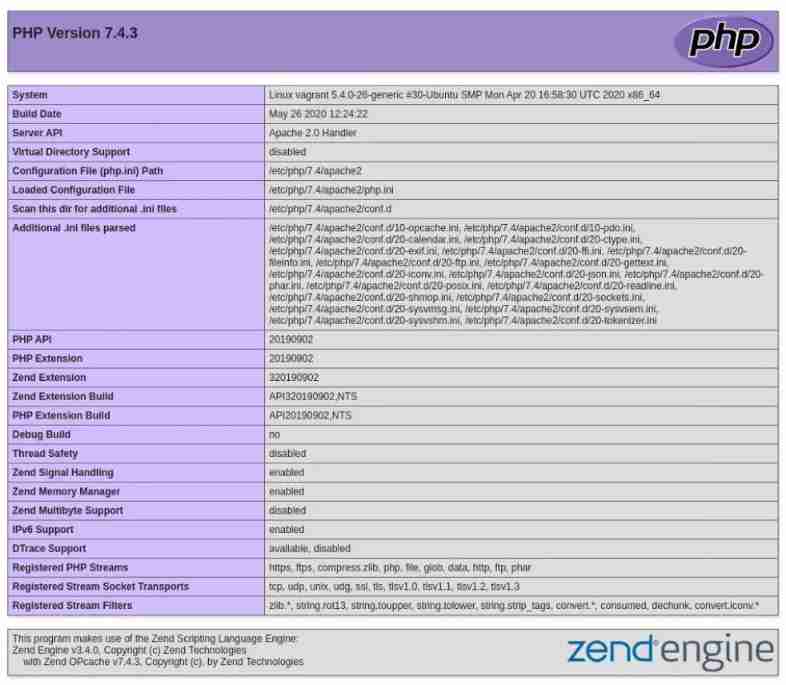
How to install PHP on Ubuntu 20.04

面试官:值为 nil 为什么不等于 nil ?
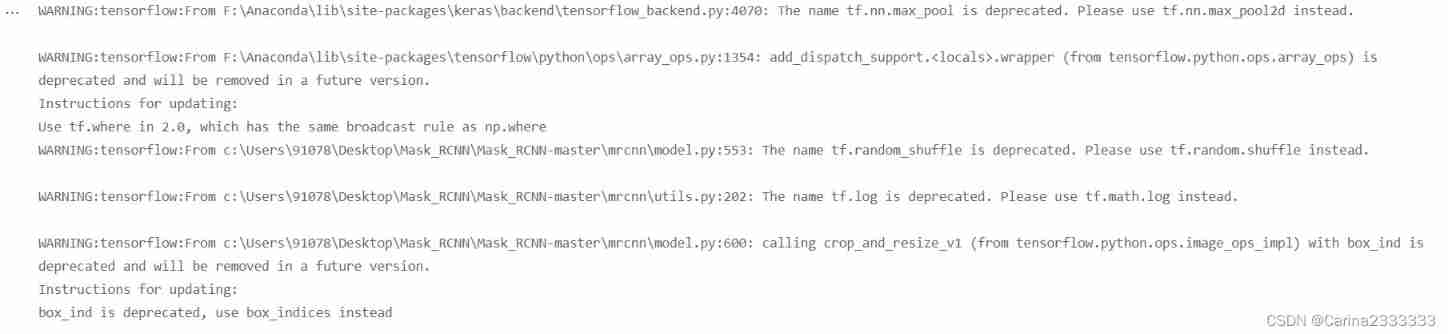
How to train mask r-cnn model with your own data

Is AI too slow to design pictures and draw illustrations? 3 sets of practical brushes to save you

Automata and automatic line of non-standard design

【RT-Thread】nxp rt10xx 设备驱动框架之--Audio搭建和使用
![Luogu: p2685 [tjoi2012] Bridge](/img/f5/f77027288a211ae466781b09ce650f.jpg)
Luogu: p2685 [tjoi2012] Bridge

Implementation of Tetris in C language
随机推荐
自动渗透测试工具核心功能简述
ArrayList分析3 : 删除元素
Kubernetes resource object introduction and common commands (4)
vs2013已阻止安装程序,需安装IE10
Electronic Science and technology 20th autumn "Microcomputer Principle and application" online assignment 2 [standard answer]
Global and Chinese health care OEM and ODM market status survey and investment planning recommendations report 2022-2028
Assignment examination questions of advanced English (III) for the course examination of Fujian Normal University in February 2022
Implementation of Tetris in C language
UE4 official charging resources, with a total price of several thousand
聊聊支付流程的设计与实现逻辑
互聯網醫院HIS管理平臺源碼,在線問診,預約掛號 智慧醫院小程序源碼
Hongmeng fourth training
Detailed explanation of common network attacks
ArrayList analysis 3: delete elements
Research Report on market demand and investment planning for the development of China's office chair industry, 2022-2028
Y is always discrete and can't understand, how to solve it? Answer: read it several times
Kotlin的協程:上下文
What is the difference between cloud server and cloud virtual machine
Deops入门
Play with fancy special effects. This AE super kit is for you