Segment tree,,

Problems solved by line segment tree

Suppose you give an array , The length is 1000, requirement 1~200 All numbers in the range increase uniformly 6;7 ~ 375 All numbers on the range are updated to 4; Inquire about 3 ~ 999 The cumulative sum of all numbers in the range .

therefore , The problem solved by the segment tree is ：

1. The unity on the interval increases add
2. Unified update on interval update
3. Accumulation and unified query on interval query

Violent solution

Violent solutions can only be traversed , The time complexity is undoubtedly O(N)

A special case

Most of the time , You don't need to use all the structures in the line segment tree in a problem , That is, it doesn't have to be used at the same time add、update、query, It's more difficult , Because to make sure add and update When used alone, they should be independent of each other , Don't fight

Segment trees also have non recursive versions , But the non recursive version is too difficult , And recursive version can solve all problems , Generally, you don't have to worry about the explosion of the stack when using the recursive version , Because the depth will not be particularly large .

Create a tree like structure

In the line tree , Array subscripts are generally from 1 Start counting .

Any node i The parent of is i / 2,
Any node i My left child is 2 * i, The right child is 2 * i + 1
Because the subscript is from 1 Start counting , It's kind of like a pile .

When the length of an array is an even number

When the array length is an odd number

How long does the requested array need to be

The length of the array is 2 To the power of , Space saving , Just prepare 2N An array of lengths ;

The length of the array is 2 To the power of +1 When , The most wasted space , But you just need to prepare 4N Just an array of length .

Why? ？ Because the number of nodes at the bottom of the binary tree be equal to Add the number of nodes of all layers from the bottom to the top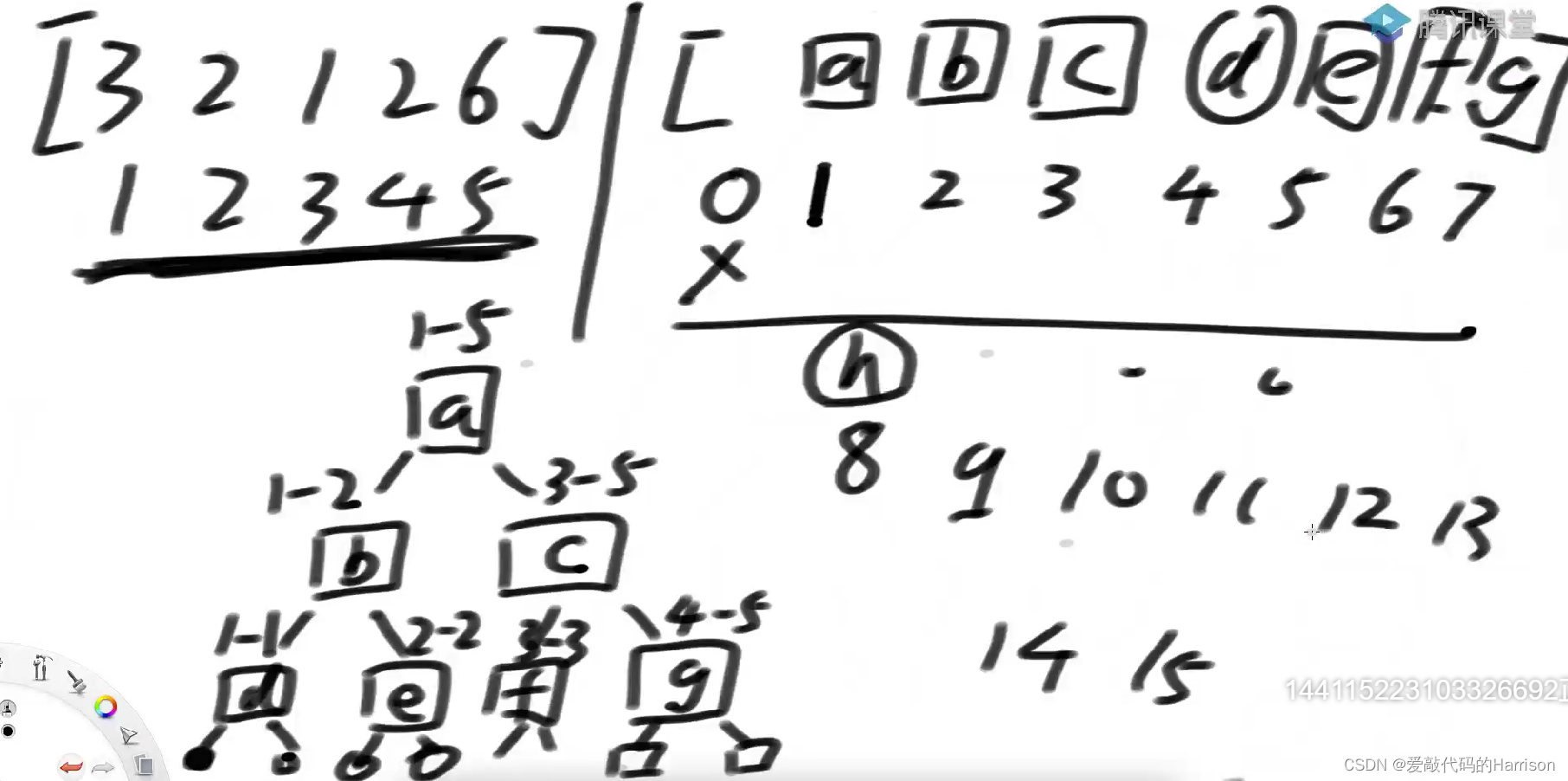

Time complexity of segment tree

O(logN)

Realize the three operations of the line segment tree on the imaginary physical structure

add operation

The original array , Prepare a cumulative sum array and an array of lazy information
In the array 1 ~ 4 Add 3

1 ~ 2 Each value in the range is added 4

How to get the sum of the accumulation of any node

The cumulative sum of the left child plus the cumulative sum of the right child

private void pushUp(int rt){
    
            sum[rt]=sum[rt<<1]+sum[rt<<1|1];
        }

Building a binary tree （ I imagined a tree like structure ）

//  In the initialization phase , The first sum Fill in the array 
        //  stay arr[l~r] In terms of scope , Go to build,1~N
        // rt： The range is sum Subscript in !!!
        //  Range and subscript are decoupled , In other words, the first two parameters are not associated with the third parameter 
        public void build(int l,int r,int rt){
    
            if(l==r){
    
                sum[rt]=arr[l];
                return ;
            }
            int mid=(l+r)>>1;
            build(l,mid,rt<<1);
            build(mid+1,r,rt<<1|1);
            pushUp(rt);
        }

Lazy update

The time complexity of line segment tree is O(logN) The key embodiment of , After a task comes down , Stick to a left border and go down once , Get stuck on a right border and go down once .

When a new task comes , First check whether the current range has been lazy , If there is , First send the lazy information to the next layer , Then deal with new tasks （ But what is implemented in the code is to accumulate the new task with the information that has been lazy before , That is to say, the previous lazy messages will not be sent first ）

When can I use a segment tree

You can get a message on the left , You can get some information on the right , The information of the parent node can be divided into the left and right information in O(1) Processed in time , And there is no need to investigate the bottom situation , This kind of interval query , Interval update , Interval addition problem , You can use the line tree .

package com.harrison.class21;

/** * @author Harrison * @create 2022-03-31-22:40 * @motto  looking for him for thousand times in the crowd , Suddenly look back , The man was in the dim light . */
public class Code01_SegmentTree {
    
    public static class SegmentTree {
    
        // arr[]  For the original sequence information from 0 Start , But in arr It's from the inside 1 At the beginning 
        // sum[]  Simulated line segment tree maintains intervals and 
        // lazy[]  Cumulative and lazy markers 
        // change[]  Updated value 
        // update[]  Update lazy tag 
        private int MAXN;
        private int[] arr;
        private int[] sum;
        private int[] lazy;
        private int[] change;
        private boolean[] update;// true： Indicates that the information on the location is valid , Otherwise it will not work 

        public SegmentTree(int[] origin) {
    
            MAXN = origin.length + 1;
            arr = new int[MAXN]; //arr[0] no need , from 1 Start using 
            for (int i = 1; i < MAXN; i++) {
    
                arr[i] = origin[i - 1];
            }
            sum = new int[MAXN << 2]; //  To support the concept of brain tonic , The accumulation and information of a certain range 
            lazy = new int[MAXN << 2]; //  To support the concept of brain tonic , There is no cumulative task passed down in a certain range 
            change = new int[MAXN << 2]; //  To support the concept of brain tonic , A task with no update operation in a certain range 
            update = new boolean[MAXN << 2]; //  To support the concept of brain tonic , A scope update task , What did the update become 
        }

        private void pushUp(int rt) {
    
            sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
        }

        //  Previous , All laziness increases , And lazy update , From the parent range , Send it to the left and right sub ranges 
        //  What is the distribution strategy 
        // ln The number of nodes on the left side of the tree represents ,rn Represents the number of nodes in the right subtree 
        //  This method is to distribute the previous lazy information 
        public void pushDown(int rt, int ln, int rn) {
    
            //  Be sure to check whether there is update, Then check whether there is cumulative sum 
            if (update[rt]) {
    //  If the parent node has an update 
                //  Both left and right children are changed to true
                update[rt << 1] = true;
                update[rt << 1 | 1] = true;
                // change  The left and right children are changed to the information of the parent node 
                change[rt << 1] = change[rt];
                change[rt << 1 | 1] = change[rt];
                //  The lazy information left by the left and right children is invalid 
                lazy[rt << 1] = 0;
                lazy[rt << 1 | 1] = 0;
                //  The accumulation and information of left and right children are also covered 
                sum[rt << 1] = change[rt] * ln;
                sum[rt << 1 | 1] = change[rt] * rn;
                update[rt] = false;
            }
            if (lazy[rt] != 0) {
    
                lazy[rt << 1] += lazy[rt];
                sum[rt << 1] += lazy[rt] * ln;
                lazy[rt << 1 | 1] += lazy[rt];
                sum[rt << 1 | 1] += lazy[rt] * rn;
                lazy[rt] = 0;
            }
        }


        //  In the initialization phase , The first sum Fill in the array 
        //  stay arr[l~r] In terms of scope , Go to build,1~N
        // rt： The range is sum Subscript in !!!
        //  Range and subscript are decoupled , In other words, the first two parameters are not associated with the third parameter 
        public void build(int l, int r, int rt) {
    
            if (l == r) {
    
                sum[rt] = arr[l];
                return;
            }
            int mid = (l + r) >> 1;
            build(l, mid, rt << 1);
            build(mid + 1, r, rt << 1 | 1);
            pushUp(rt);
        }

        // L~R ->  The scope of the mission ,  All values become C
        // l,r ->  The scope of expression 
        // rt ->  Where to find it l,r Information on scope 
        public void update(int L, int R, int C, int l, int r, int rt) {
    
            //  The scope of the mission completely covers , The scope of the current expression 
            if (L <= l && r <= R) {
    
                update[rt] = true;
                change[rt] = C;
                sum[rt] = C * (r - l + 1);
                lazy[rt] = 0;
                return;
            }
            //  The current task does not include l...r All encompassing , We should send the current task down 
            //  Why is midpoint required ？ Because there are several numbers on the left and right 
            int mid = (l + r) >> 1;// l...mid (rt<<1) mid+1...r (rt<<1|1)
            //  All the lazy tasks saved before distribution 
            pushDown(rt, mid - l + 1, r - mid);
            //  Whether the left child needs to receive a task 
            if (L <= mid) {
    
                update(L, R, C, l, mid, rt << 1);
            }
            //  Does the right child need a task 
            if (R > mid) {
    
                update(L, R, C, mid + 1, r, rt << 1 | 1);
            }
            //  After the children finish the task , Update my sum Information 
            pushUp(rt);
        }

        // L~R ->  The scope of the mission , All the values add up to C
        // l,r ->  The scope of expression 
        // rt ->  Where to find it l,r Information on scope 
        public void add(int L, int R, int C, int l, int r, int rt) {
    
            //  The scope of the mission completely covers , The scope of the current expression 
            if (L <= l && r <= R) {
    
                sum[rt] += C * (r - l + 1);
                lazy[rt] += C;
                return;//  If you are lazy, don't send it , The key to excellent time complexity 
            }
            //  The current task does not include l...r All encompassing , We should send the current task down 
            //  Why is midpoint required ？ Because there are several numbers on the left and right 
            int mid = (l + r) >> 1;// l...mid (rt<<1) mid+1...r (rt<<1|1)
            //  All the lazy tasks saved before distribution 
            pushDown(rt, mid - l + 1, r - mid);
            //  Whether the left child needs to receive a task 
            if (L <= mid) {
    
                add(L, R, C, l, mid, rt << 1);
            }
            //  Does the right child need a task 
            if (R > mid) {
    
                add(L, R, C, mid + 1, r, rt << 1 | 1);
            }
            //  After the children finish the task , Update my sum Information 
            pushUp(rt);
        }

        // 1~6  How much is the cumulative sum ？ 1~8 rt
        public long query(int L, int R, int l, int r, int rt) {
    
            if (L <= l && r <= R) {
    
                return sum[rt];
            }
            int mid = (l + r) >> 1;
            pushDown(rt, mid - l + 1, r - mid);
            long ans = 0;
            if (L <= mid) {
    
                ans += query(L, R, l, mid, rt << 1);
            }
            if (R > mid) {
    
                ans += query(L, R, mid + 1, r, rt << 1 | 1);
            }
            return ans;
        }
    }

    public static class Right {
    
        public int[] arr;

        public Right(int[] origin) {
    
            arr = new int[origin.length + 1];
            for (int i = 0; i < origin.length; i++) {
    
                arr[i + 1] = origin[i];
            }
        }

        public void update(int L, int R, int C) {
    
            for (int i = L; i <= R; i++) {
    
                arr[i] = C;
            }
        }

        public void add(int L, int R, int C) {
    
            for (int i = L; i <= R; i++) {
    
                arr[i] += C;
            }
        }

        public long query(int L, int R) {
    
            long ans = 0;
            for (int i = L; i <= R; i++) {
    
                ans += arr[i];
            }
            return ans;
        }

    }

    public static int[] genarateRandomArray(int len, int max) {
    
        int size = (int) (Math.random() * len) + 1;
        int[] origin = new int[size];
        for (int i = 0; i < size; i++) {
    
            origin[i] = (int) (Math.random() * max) - (int) (Math.random() * max);
        }
        return origin;
    }

    public static boolean test() {
    
        int len = 100;
        int max = 1000;
        int testTimes = 5000;
        int addOrUpdateTimes = 1000;
        int queryTimes = 500;
        for (int i = 0; i < testTimes; i++) {
    
            int[] origin = genarateRandomArray(len, max);
            SegmentTree seg = new SegmentTree(origin);
            int S = 1;
            int N = origin.length;
            int root = 1;
            seg.build(S, N, root);
            Right rig = new Right(origin);
            for (int j = 0; j < addOrUpdateTimes; j++) {
    
                int num1 = (int) (Math.random() * N) + 1;
                int num2 = (int) (Math.random() * N) + 1;
                int L = Math.min(num1, num2);
                int R = Math.max(num1, num2);
                int C = (int) (Math.random() * max) - (int) (Math.random() * max);
                if (Math.random() < 0.5) {
    
                    seg.add(L, R, C, S, N, root);
                    rig.add(L, R, C);
                } else {
    
                    seg.update(L, R, C, S, N, root);
                    rig.update(L, R, C);
                }
            }
            for (int k = 0; k < queryTimes; k++) {
    
                int num1 = (int) (Math.random() * N) + 1;
                int num2 = (int) (Math.random() * N) + 1;
                int L = Math.min(num1, num2);
                int R = Math.max(num1, num2);
                long ans1 = seg.query(L, R, S, N, root);
                long ans2 = rig.query(L, R);
                if (ans1 != ans2) {
    
                    return false;
                }
            }
        }
        return true;
    }

    public static void main(String[] args) {
    
        int[] origin = {
    2, 1, 1, 2, 3, 4, 5};
        SegmentTree seg = new SegmentTree(origin);
        int S = 1; //  The starting position of the whole section , The rules are from 1 Start , Not from 0 Start  ->  Fix 
        int N = origin.length; //  The end position of the whole interval , Regulations can arrive N, No N-1 ->  Fix 
        int root = 1; //  The position of the head node of the whole tree , The rule is 1, No 0 ->  Fix 
        int L = 2; //  The starting position of the operation section  ->  variable 
        int R = 5; //  The end position of the operation section  ->  variable 
        int C = 4; //  The number to be added or updated  ->  variable 
        //  Interval generation , Must be in [S,N] On the whole range build
        seg.build(S, N, root);
        //  Interval modification , You can change L、R and C Value , Other values cannot be changed 
        seg.add(L, R, C, S, N, root);
        //  Interval update , You can change L、R and C Value , Other values cannot be changed 
        seg.update(L, R, C, S, N, root);
        //  Interval query , You can change L and R Value , Other values cannot be changed 
        long sum = seg.query(L, R, S, N, root);
        System.out.println(sum);

        System.out.println(" Logarithm test starts ...");
        System.out.println(" test result  : " + (test() ? " adopt " : " Not through "));

    }
}