固体火箭发动机三维装药逆向内弹道计算

什么是逆向内弹道计算？

通常的内弹道计算是已知燃面面积随烧去肉厚的变化曲线($A_{\mathrm{b}}-w$)之后再计算燃烧室压力随时间变化的曲线($p_{\mathrm{c}}-t$)。而逆向内弹道计算即是已知$p_{\mathrm{c}}-t$后计算$A_{\mathrm{b}}-w$。逆向内弹道计算对装药设计有重要指导作用

计算公式

平衡状态下，燃烧室的压力计算方法为
$$p_{\mathrm{c}}={\left(a{c}^{\ast }{\rho }_{\mathrm{p}}\frac{A_{\mathrm{b}}}{A_{\mathrm{t}}}\right)}^{\frac{1}{1-n}}$$
可以解得
$$A_{\mathrm{b}}=A_t\frac{{p_{\mathrm{c}}}^{1-n}}{a{c}^{\ast }{\rho }_{\mathrm{p}}}$$
燃烧肉厚可以通过积分得到
$$w=\underset{0}{\overset{t}{\int }}a{p}_{\mathrm{c}}{\left(\tau \right)}^n\mathrm{d}\tau$$

无量纲化

无量纲燃面面积为
$${A_{\mathrm{b}}}^{+}C=\frac{A_{\mathrm{b}}}{\pi R^2}\frac{\pi R^2}{A_t}=\frac{{p_{\mathrm{c}}}^{1-n}}{a{c}^{\ast }{\rho }_{\mathrm{p}}}$$
无量纲燃烧肉厚为
$$w^{+}=\frac{w}{R}=\frac{\underset{0}{\overset{t}{\int }}a{p}_{\mathrm{c}}{\left(\tau \right)}^n\mathrm{d}\tau }{R}$$
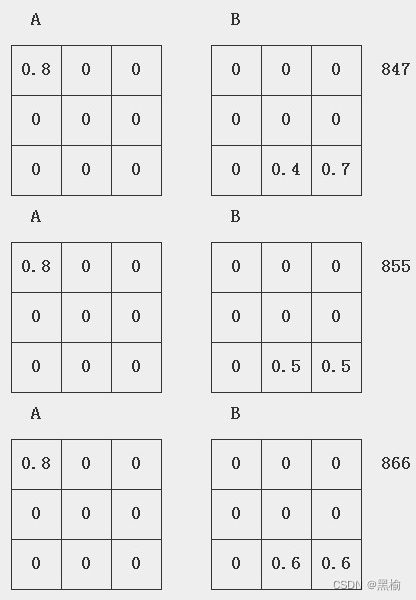
对于任意两个几何相似的装药，将拥有相同的${A_{\mathrm{b}}}^{+}-w^{+}$曲线