神经网络迭代次数的一个近似关系

(A，B)---m*n*k---(1,0)(0,1)

移位距离和假设

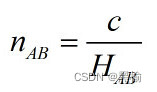
用神经网络分类A和B，把参与分类的A和B中的数字看作是组成A和B的粒子，分类的过程就是让A和B中的粒子互相交换位置，寻找最短移位路径的过程。而熵H与最短移位距离和成正比，迭代次数n和熵H成反比。

对二值化图片移位规则汇总

每个粒子移位一次，位置重合不移位，0不动，单次移位距离恒为1.

按照移位距离和假设，二值化图片的移位元素单次移动的距离恒为1.而1也恰好是该移位元素的数值。所以这是否意味着对于更一般的图片，单次移位的距离就是元素数值本身？

这次就实验验证这一猜测，

用神经网络分类844，835，836，固定收敛误差取迭代次数平均值，每个收敛误差统计199次，得到迭代次数如下

	844	835	836
δ	迭代次数n	迭代次数n	迭代次数n
5.00E-04	35833.36	35043.31	33397.4
4.00E-04	43599.63	42545.46	40815.2
3.00E-04	56517.97	55280.16	53150.44
2.00E-04	80381.21	79393.91	75799.5
1.00E-04	151755.1	150807.4	142995.6

为验证是否存在数值上的加和关系做第二组实验

分类8134，8125，8126比较两组数值

 如果假设是对的则8134，可以理解为0.1+0.3=0.4，则8134=844.同样8125可以理解为0.1+0.2=0.3，则8125化为835.同样8126可化为836.比较这三组数是否有这样的近似关系

	8134	8125	8126
δ	迭代次数n	迭代次数n	迭代次数n
5.00E-04	37066.05	36145.16	33883.76
4.00E-04	45113.94	43319.59	41075.22
3.00E-04	58249.69	56453.31	53234.41
2.00E-04	84504.05	81537.82	77773.45
1.00E-04	157462.3	153052.5	144980.9
	844	835	836
δ	迭代次数n	迭代次数n	迭代次数n
5.00E-04	35833.36	35043.31	33397.4
4.00E-04	43599.63	42545.46	40815.2
3.00E-04	56517.97	55280.16	53150.44
2.00E-04	80381.21	79393.91	75799.5
1.00E-04	151755.1	150807.4	142995.6

通过数据比较，这几组数据之间确实很接近

做第三组实验

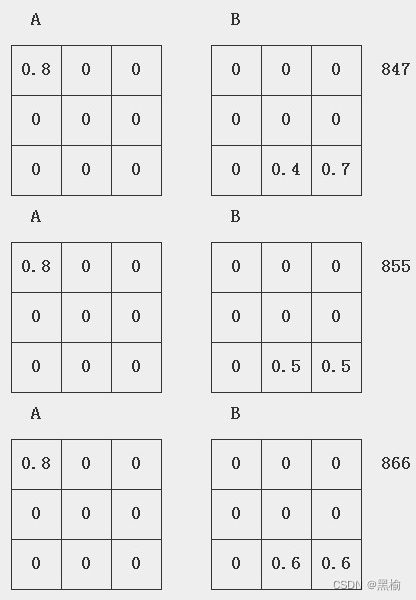
分类847，855，866，

对照实验

分类8227，8235，8246.同样8227可以理解为0.2+0.2=0.4，变为847.8235由0.2+0.3=0.5，化为855.而8246由0.2+0.4=0.6，化为866.比较两组的迭代次数

	8227	8235	8246
δ	迭代次数n	迭代次数n	迭代次数n
5.00E-04	32227.51	34556.86	32508.18
4.00E-04	39270.1	42118.01	39387.94
3.00E-04	50701.36	54289.11	51212.08
2.00E-04	73393.27	78316.52	73658.53
1.00E-04	139882	146499.2	140009.1
	847	855	866
δ	迭代次数n	迭代次数n	迭代次数n
5.00E-04	31618.62	33055.99	31281.7
4.00E-04	38436.06	39901.37	38625.74
3.00E-04	50189.28	51460.66	49455.25
2.00E-04	71974.27	74893.88	71792.71
1.00E-04	136718.7	142850.2	134001.6

除了8246和866这两组差别较大，另外两组相差很小。

将两组数据放在一起比较

	8134	8125	8126	8235	8227	8246
δ	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n
5.00E-04	37066.05	36145.16	33883.76	34556.86	32227.51	32508.18
4.00E-04	45113.94	43319.59	41075.22	42118.01	39270.1	39387.94
3.00E-04	58249.69	56453.31	53234.41	54289.11	50701.36	51212.08
2.00E-04	84504.05	81537.82	77773.45	78316.52	73393.27	73658.53
1.00E-04	157462.3	153052.5	144980.9	146499.2	139882	140009.1
	844	835	836	855	847	866
δ	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n
5.00E-04	35833.36	35043.31	33397.4	33055.99	31618.62	31281.7
4.00E-04	43599.63	42545.46	40815.2	39901.37	38436.06	38625.74
3.00E-04	56517.97	55280.16	53150.44	51460.66	50189.28	49455.25
2.00E-04	80381.21	79393.91	75799.5	74893.88	71974.27	71792.71
1.00E-04	151755.1	150807.4	142995.6	142850.2	136718.7	134001.6

画成图

1.00E-04	151755.1	150807.4	142995.6	142850.2	136718.7	134001.6
1.00E-04	157462.3	153052.5	144980.9	146499.2	139882	140009.1

这次实验用神经网络分类0.8和3x与0.8和2y，并且让x1+x2+x3=y1+y2。迭代次数分别是n3x和n2y。实验表明n3x和n2y之间可能存在n3x=a*n2y (a>1）这样的近似关系。