【Day6-7 文献精读】A unifying Bayesian framework accounting for spatiotemporal interferences with a ...

阅读文献：

Chen, Y., et al. (2021). "A unifying Bayesian framework accounting for spatiotemporal interferences with a deceleration tendency." vision research 187: 66-74.

文献链接：A unifying Bayesian framework accounting for spatiotemporal interferences with a deceleration tendency - ScienceDirect

本文为Day1文献的后续研究，两篇应结合阅读。

文章目录

• 摘要
• 一、前言
• 二、实验一
• 三、实验二
• 四、总结

---

摘要

1、本研究将Kappa效应的经典模型与贝叶斯框架结合，提出一个新的对数版经典模型；

2、Kappa效应增速减缓的趋势受韦伯定律的影响（而非慢速度模型中认为的空间不确定性）；

3、为时空干扰的机制提供了新的见解。

---

一、前言

1、Kappa效应：一种时空干扰效应，两刺激出现的时间间隔随二者的距离增加而增加，且呈现增速减缓的趋势。

2、解释Kappa效应的2种理论模型：

（1）经典模型（classical model）：将Kappa效应归结于恒定速度。观察者认为不连续出现的刺激是以恒定速度移动的，知觉到的时间间隔是实际时间和期望时间的加权平均（见Day1文献的前言），且与刺激间距离呈线性正向关系；

（2）慢速度模型（slowness model）：将Kappa效应归结于慢速度。模型运用了贝叶斯法则并基于“慢速度先验”假设，来源于物体运动的统计结构，即物体倾向于以慢速度在背景中运动。刺激呈现位置的不确定性是造成Kappa效应增速减缓趋势的原因。

3、在Day1的文献中发现：

（1）在恰当定义情况下，经典模型可以表述为贝叶斯模型的形式；

（2）在拟合数据时两种模型都能复制被试反应，但慢速度模型能更好预测行为；

（3）慢速度模型的3个缺点：1）复杂；2）空间不确定性（spatial uncertainty，Day1文献中为spatial variances）为估算值且假定不变；3）对新的样本时间估计时应用受限。

（4）Kappa效应是慢速度导致，增速减缓趋势受空间不确定性调节，但此假设并未进行验证。

4、韦伯（-费希纳）定律显示了一种典型的减速趋势，即主观感觉与刺激强度的对数成正比。因而本文假设Kappa效应中的增速减缓趋势由韦伯（-费希纳）定律驱动。

5、本文根据一个运用了韦伯（-费希纳）定律、能用于对量级（如距离等）进行估计的贝叶斯框架（A unifying Bayesian framework），与经典模型整合提出了个对数版logarithmic version的经典模型LCM：

（1）LCM：物理时间和期望时间被对数化转化为内部时间，估计的内部时间是物理时间和期望时间的加权平均；

（2）经典模型CM：估计时间是物理时间和期望时间的加权平均。

对于两篇文献中涉及到的几种跟时间有关的概念，各自有不同的表述，以下作对照梳理：

英文	中文
internal time=measured time=perceived time	内部时间=测量时间=感觉时间
estimated time(CM)≈estimated internal time(LCM) =perceptual time	估计时间=知觉时间
sample time=actual time=physical time	样本时间=实际时间=物理时间

---

二、实验一

1、实验目的：验证估计时间是否受空间变异性影响（从而造成Kappa效应增速减缓）。

2、实验设计：

20名被试参与3（两圆水平距离，0°/4°/8°）×3（两圆垂直距离，0°/4°/8°）×7（比较时距时长，即蓝方块呈现时长0.2s-0.8s）被试内实验设计。屏幕上将间隔0.5s（样本时距）相继呈现两圆，分别位于屏幕左面及右面，其水平和垂直距离各有3个水平，因此有9种位置组合；在两圆呈现之前或之后呈现蓝色方块（7种时长），被试需比较样本时距和比较时距哪个更长。流程与结果如下图：

3、从Fig 1的C-E可得：

（1）对于水平距离：三个模型均预测估计时间随水平距离增大而增大；

（2）对于垂直距离：

        1）class model和LCM：估计时间与水平距离无关；

        2）slowness model：垂直距离越大离心率越大→位置（空间）不确定性越大→对物理距离低估→知觉到更短的时距，因而考虑了空间变异性的慢速度模型预测估计时间随垂直距离增大而减小。

在此我有两个疑问：

1、在慢速度模型中，为什么离心率和空间不确定性只针对两圆间的垂直距离？在水平距离和垂直距离增大时对估计时间的影响作用相反？

猜想：离心率是基于二者的相对位置提出的（参考Fig 1的B），水平距离上的变化不会改变二者位于同一水平线上的情况，而垂直距离增加会导致二者连线与水平线出现夹角，因而导致离心率变化？（我的想法还是太表层太不专业了...）

文中解释：偏心率空间不确定性的增加被认为是由于视网膜-皮层成像精度的降低(Klein & Levi, 1987;Levi & Klein, 1990)，以及视网膜马赛克空间不规则性的增加引起的(Wilson, 1991)，因而认为垂直位移增加空间不确定性是合理的。

2、本实验采用的比较时距任务，估计时间是怎么得到的呢？（模型计算？）

4、数据处理：

对每种处理的数据用累积高斯函数进行拟合，主观相等点the point of subjective equality (PSE)和标准差使用最佳拟合函数the best-ftting function进行计算，Fig 2中A-C为一个典型被试在9种处理条件（3水平3垂直）下的结果；对所有被试的PSE和SD（均值）分别做两因素重复测量方差分析，因素为水平、垂直距离，得D-F：

5、结果和讨论

（1）PSE：

        1）从Fig 2的A-C，被试的心理测量曲线都随水平距离增大而右移，从Fig 2的D，PSE随水平距离增大时增大，而垂直距离增大时保持不变；

        2）对PSE的方差分析结果显示：

        ① 水平距离主效应显著，0°时PSE显著小于4°和8°，4°时PSE显著小于8°，与典型Kappa效应一致；

        ② 垂直距离、水平距离与垂直距离交互作用不显著，这与慢速度模型预测估计时间将随垂直距离增大而减小的观点不一致。

        ③ 对垂直距离的主效应进一步做统计效力分析，显示垂直距离对估计时间的效应非常微弱。

        综合结果显示，垂直距离对估计时间无影响，即空间变异性不是影响Kappa效应的原因。

此部分将PSE与估计时间进行等同，原因：PSE意味着被试认为比较时距与标准（样本）时距相同，比较时距就等同于被试对样本时间的估计时间。

（2）SD：

        1）对SD的方差分析结果显示：

        ① 水平距离、垂直距离和二者交互作用不显著；

        ② 平均SD随水平距离增加呈增加趋势，统计效应力分析显示，当样本量增加到合适水平，水平距离对SD的主效应可以变得显著。

（3）PSE与SD的相关关系：

计算皮尔逊相关系数，显示二者呈显著正向相关，与标量变异性scalar variability一致（内部时间的标准差随其平均值线性增加）。

---

三、实验二

1、实验目的：验证Kappa效应增速减缓是否受韦伯-费希纳定律影响。

2、实验设计：

10名被试参与2（样本时距，0.5 or 1 s）×6（样本间隔距离，1°, 2°, 4°, 8°, 16°, or 32°）×2（比较刺激时距类型，阶梯增加or减少）被试内实验设计。样本刺激的两个小圆相继在屏幕左右侧呈现，时距为0.5或1秒，水平距离有6种，垂直距离不变；比较刺激在样本刺激之前或之后呈现，其两圆的空间距离不变，比较时距呈阶梯增加（以标准时距0.4倍为起点，步长0.1秒增加）或阶梯减少（以标准时距1.6倍为起点，步长0.1秒），要求被试对样本时距和比较时距进行判断任务，并根据交错自适应阶梯法对比较调整，如增加过程中若判断任务正确则一直按步长增加直到判断错误，下一次在此时比较时距的基础上按步长递减继续判断。

3、模型拟合数据

（1）本实验使的因变量仍为被试判断的主观相等点PSE和标准差SD。对每个处理和每个参与者的数据通过累积高斯函数拟合得到PSE，见下图：

（2）经典模型和LCM的拟合被试时间判断任务的三个阶段：

        1）对于经典模型（Fig 3的B）

        ① Measurement：当外界呈现的刺激信息ts1（样本时间sample time）进入到大脑中时，伴随着加工信息的噪音，在脑里面形成一个感觉记忆表征（测量时间measured time）tm1；

        ② Estimation：根据贝叶斯定理，由先前经验（prior，先验）和感觉记忆表tm1（likelihood，似然性）整合得到一个后验时间（posterior，后验），即知觉到的时间（估计时间estimated time）te1；

        ③ Decision：将te1与通过相同过程基于比较时距得到的te2进行比较，通过信号检测论进行决策判断，得到p(比较时距te2＞样本时距te1)的累加概率分布，其计算公式为：

        

       其中，在第i个试次，被试认为比较时距小于样本时距，ri=-1，反之ri=+1； d'为时间判断任务的表现，根据标准信号检测论计算，公式及推导过程见附录（此部分还看不太懂，还需进一步学习）；Ф为累积标准正态分布函数。

        2）对于LCM（Fig 3的C）：假定刺激信息刚进入大脑时为对数正态分布tm1，需先进行对数转化为sm1形成感觉记忆表征，随后的过程与经典模型相同。

        3）在Day1文献中经典模型拟合被试复制时间任务的第三阶段为时间复制，而本实验为时间判断，两部分可对照起来理解。

参考：

科学网—空间信息如何影响时间知觉？贝叶斯模型告诉您答案 - 陈有国的博文

（3）假设试次间的反应是独立的，则所有n个试次反应的联合条件概率为：

其中，经典模型的3个参数θ分别为： ω, v0, wm；LCM的4个参数θ分别为：ωs, σsm,v0, t0。

（4）The Akaike information criterion (AIC)：用于计算模型的拟合情况，其值约小越好

θ为经典模型CM和LCM模型用最大似然化法估计的最佳拟合参数，k为参数个数。

4、结果与讨论

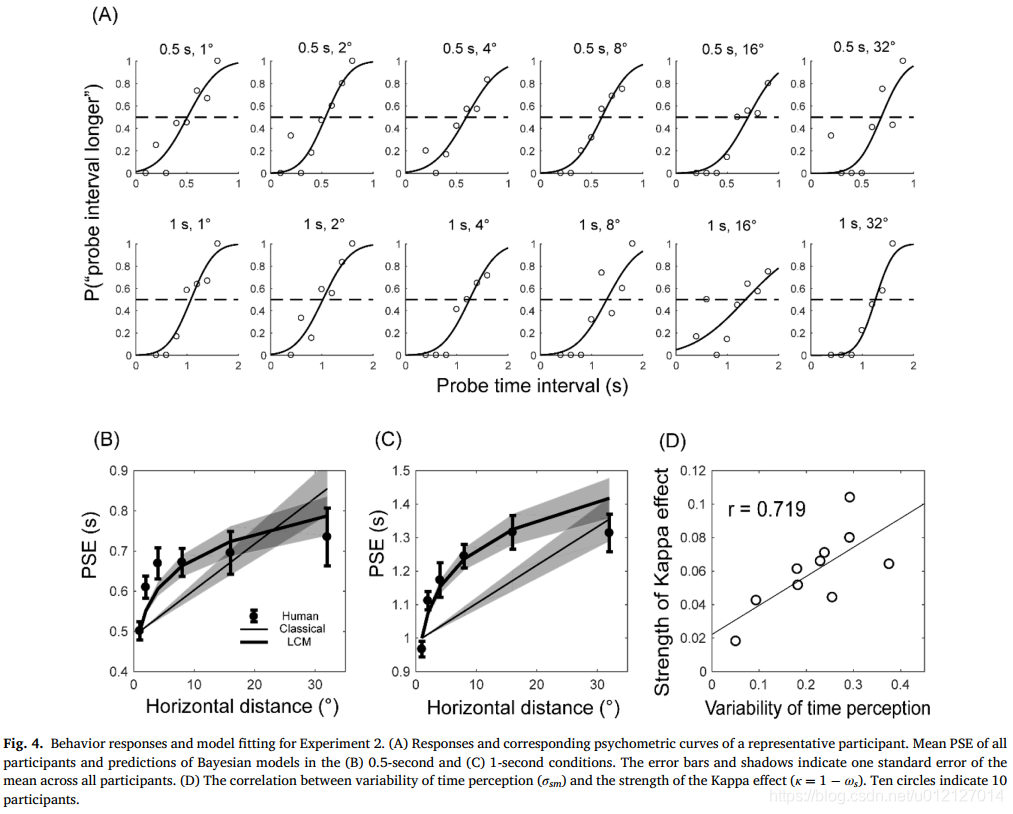
（1）从图Fig 4的A，在12种处理（2时距×6水平距离）下对一典型被试的PSE进行估计，当水平距离增加，被试心理测量曲线右移；

（2）从图Fig 4的B和C，被试的PSE（估计时间）在0.5s和1s时距条件下都出现增速减缓趋势，LCM（PSE是两圆间距离的幂函数）比经典模型（PSE是两圆间距离的线性函数）更好地拟合被试数据；

（3）基于LCM对Kappa效应的个体差异进行探讨，定义一个关于Kappa效应强度的指标κ，κ越大代表随着两圆间距离l增加，估计时间增加越快，其公式为：

其中， σsm为时间知觉的变异性。

从Fig 4的D，Kappa效应强度κ与时间知觉的变异性σsm存在显著正相关。

（4）模型拟合情况AIC：

AIC difference (Δ)=AICcm-AIClcm∈[5.943, 24.0999]

参照经验标准(0 ≤ Δ ≤ 2 =substantial; 4 ≤ Δ ≤ 7 = considerably less; Δ > 10 = essentially none;)

对于所有被试，LCM在模型拟合方面优于经典模型。

---

四、总结

1、实验一证明Kappa效应中增速减缓趋势不受刺激空间不确定性驱动，此结果与通过触觉研究中的慢速度模型不符，原因可能是感觉通道不同。视觉的空间敏锐度高于触觉，更不易受期望的干扰，因而慢速度模型不适用于解释视觉的Kappa效应。

2、实验二证明对数版的经典模型LCM比拟合数据能力优于经典模型，LCM能预测Kappa效应增速减缓的趋势，认为时间的感觉记忆表征（内部时间）由样本时间对数转化而来，符合韦伯-费希纳定律。本研究提出Kappa效应的增速减缓趋势受韦伯-费希纳定律驱动。

3、本研究采用了时间比较任务，而非Day1文献的时间复制任务，能避免被试在复制时间时产生的误差，更适用于对Kappa效应的研究。

4、经典模型和LCM都是基于恒定速度，通过计算两模型得到的恒定速度都接近于人的绝对速度阈限，显示恒定速度是慢速度，与Day1文献结果一致。

5、本研究提出了一个衡量个体产生Kappa效应强度的指标κ，发现其与时间知觉变异性呈显著正相关，即个体的时间知觉越精确，其时间知觉变异性越低，则产生的Kappa效应越低。此结果与贝叶斯理论一致，其认为随着任务的不确定性增加，人类对先验知识的依赖也会增加。