当前位置:网站首页>deep learning statistical arbitrage
deep learning statistical arbitrage
2022-06-27 10:54:00 【SyncStudy】
deep learning statistical arbitrage
- empirial
- stanford
- Jorge guijarro
- markus
Motivation
- Pair trading
- GM and Ford
- Assumption
- prices are on average similar
- Exploit temporal price different between similiar seests
Three components of statisical arbitarge
- contrict protolio
- trading signal
Foundational problem
Research question
- arbitrage portolios
- arbitarge signals
Contributions
- Novel conceptual framework
- Unified framework
- To compare different statistical arbitrage methods
- Portolio generation
- signal extraction
- allocation decision
- Study each component and compare with conventional models
Novel methods
- statistical factor
- Convolution neural network
Empirical
- substantially outperforms
- sharpe ratios
Parametric models
- PCA
- cOINTEGRATION
- STOCHASTIC CONTROL
- SIMPLE PAIRS TRADING
- INTRACTABLE PARAMETRIC MODELS WITH ml
Model
R n , t = β n , t − 1 T F t + ε R_{n,t}=\beta^T_{n,t-1}F_t+\varepsilon Rn,t=βn,t−1TFt+ε
x : = ε t L : = ( ε n , t − L ) x:=\varepsilon_t^L:=(\varepsilon_{n,t-L}) x:=εtL:=(εn,t−L)
w t − 1 ε = w ε ( θ ( ε t − 1 L ) ) w_{t-1}^\varepsilon=w^\varepsilon(\theta(\varepsilon_{t-1}^L)) wt−1ε=wε(θ(εt−1L))
w t − 1 R = w_{t-1}^R=\frac{}{} wt−1R=
d X t = κ ( μ − X t ) dX_t = \kappa(\mu-X_t) dXt=κ(μ−Xt)
θ i = ∑ j = 1 L W j f i l t e r X j \theta_i=\sum_{j=1}^{L}W_j^{filter}X_j θi=j=1∑LWjfilterXj
W W^{} W
θ C N N + T r a n s ( X ) \theta^{CNN+Trans}(X) θCNN+Trans(X)
y I ( 0 ) = ∑ m = 1 D s i z e W m l o c a l X y_I^{(0)}=\sum_{m=1}^{D_{size}}W_m^{local}X yI(0)=m=1∑DsizeWmlocalX
h i = ∑ I = 1 L α i , I x I ~ h_i=\sum_{I=1}^{L}\alpha_i,I\widetilde{x_I} hi=I=1∑Lαi,IxI
F a m a − F r e n c h F a c t o r Fama-French Factor Fama−FrenchFactor
C N N + T r a n s f o r m CNN+Transform CNN+Transform
α , t α , R 2 \alpha, t_\alpha,R^2 α,tα,R2
t μ t_\mu tμ
w t − 1 = w t − 1 w_{t-1}=\frac{w_{t-1}^{}}{} wt−1=wt−1
L = 60 L=60 L=60
F F N FFN FFN
< 1 % <1\% <1%
T t r a i n = 4 T_{train}=4 Ttrain=4
f a s t − r e v e r s a l fast-reversal fast−reversal
- fast reversal
- early momemtum
- low frequency downturn
- low frequency momentum
- smooth trends or local curvature
- most recent 14 days get more attention for trading decision
- more complex than simple reversal patterns
c o s t ( w t − 1 R , w t − 2 R ) = 0.0005 ∣ ∣ w t − 1 cost(w_{t-1}^R, w_{t-2}^R)=0.0005||w_{t-1} cost(wt−1R,wt−2R)=0.0005∣∣wt−1
B = 7 B=7 B=7
S R = 1 SR=1 SR=1
a r b i t r a g e arbitrage arbitrage
m e a n mean mean
Δ P = P 2 − P 1 \Delta P=P_2-P_1 ΔP=P2−P1
V = ∑ V=\sum V=∑
V = ∣ β 0 + β 1 Δ P ∣ V=|\beta_0+\beta_1\Delta P| V=∣β0+β1ΔP∣
β 0 = c ( μ A − μ B ) \beta_0=c(\mu_A-\mu_B) β0=c(μA−μB)
β 1 = f ( r i s k ) \beta_1=f(risk) β1=f(risk)
E ( V ) = E [ ∣ β 0 + β 1 σ P Z ∣ ] E(V)=E[|\beta_0+\beta_{1\sigma P}Z|] E(V)=E[∣β0+β1σPZ∣]
Z Z Z
N ( 0 , 1 ) N(0,1) N(0,1)
E ( V ) = c o n s t a n t E(V)=constant E(V)=constant
1 1 + ϕ ( h ∣ β 0 ∣ β 1 ) \frac{1}{1+\phi (\frac{h|\beta_0|}{\beta_1})} 1+ϕ(β1h∣β0∣)1
K > S T K>S_T K>ST
K ≤ S τ K \le S_\tau K≤Sτ
K − S τ K-S_\tau K−Sτ
K > S 0 , k = S 0 K>S_0, k=S_0 K>S0,k=S0
m o n e y n e s s = l o g ( K S 0 ) σ τ moneyness=\frac{log(\frac{K}{S_0})}{\sigma \sqrt{\tau}} moneyness=στlog(S0K)
l o n g d a t e d = l a r g e τ long dated = large \tau longdated=largeτ
M o n e y n e s s = l o g ( K S 0 ) σ τ Moneyness = \frac{log(\frac{K}{S_0})}{\sigma\sqrt{\tau}} Moneyness=στlog(S0K)
S P X SPX SPX
3 b i l l i o n 3 billion 3billion
R V t o p t i o n = ∑ i ( r i , t o p t i o n ) 2 RV_t^{option}=\sum_i (r_{i,t}^{option})^2 RVtoption=i∑(ri,toption)2
realized variance
R V t o p t i o n = ∑ i ( r i , t o p t i o n ) 2 RV_t^{option}=\sum_i(r_{i,t}^{option})^2 RVtoption=i∑(ri,toption)2
边栏推荐
- deep learning statistical arbitrage
- C any() and aii() methods
- leetcode待做题目
- Oracle trigger stored procedure writes at the same time
- “全班29人24人成功读研”冲上热搜!剩下的5个人去哪了?
- Record in detail the implementation of yolact instance segmentation ncnn
- 闭包的常见问题
- 使用Karmada实现Helm应用的跨集群部署【云原生开源】
- torchvision. models._ utils. Intermediatelayergetter tutorial
- 数据库之元数据
猜你喜欢
![LeetCode 522 最长特殊序列II[枚举 双指针] HERODING的LeetCode之路](/img/b1/80a51b403dfb0611b87ef9aa3215af.png)
LeetCode 522 最长特殊序列II[枚举 双指针] HERODING的LeetCode之路

Mail system (based on SMTP protocol and POP3 protocol -c language implementation)

21:第三章:开发通行证服务:4:进一步完善【发送短信,接口】;(在【发送短信,接口】中,调用阿里云短信服务和redis服务;一种设计思想:BaseController;)

记一次 .NET 某物管后台服务 卡死分析

【TcaplusDB知识库】Tmonitor单机安装指引介绍(一)

在外企远程办公是什么体验? | 社区征文

学习笔记之——数据集的生成

Leetcode 729. 我的日程安排表 I(牛逼,已解决)
![leetcode:522. Longest special sequence II [greed + subsequence judgment]](/img/43/9b17e9cb5fee9d14c2986a2141889d.png)
leetcode:522. Longest special sequence II [greed + subsequence judgment]
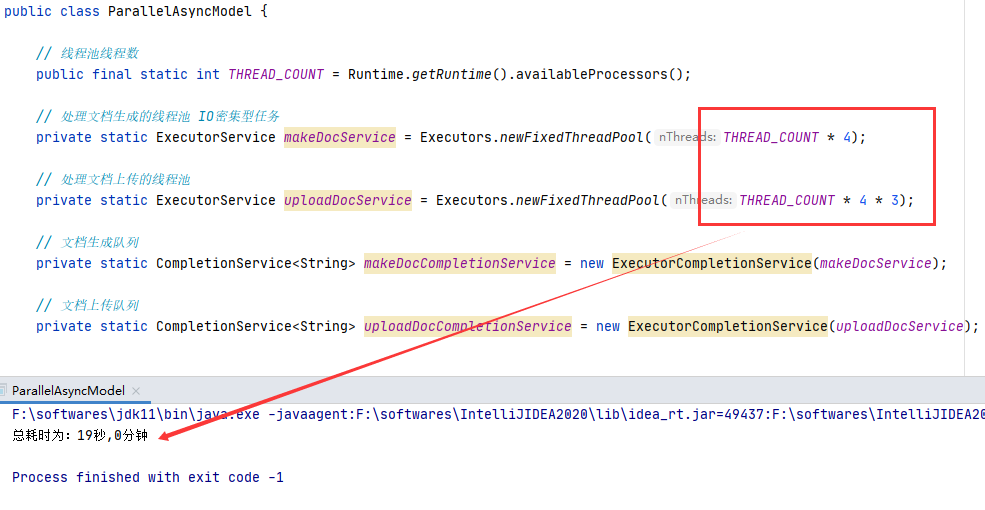
Future & CompletionService
随机推荐
Queue, two-way queue, and its application
iMeta:高颜值绘图网站imageGP+视频教程合集,已被引360次(220625更新)
Leetcode 522 longest special sequence ii[enumeration double pointer] leetcode path of heroding
Dimitt's law
[methodot topic] what kind of low code platform is more suitable for developers?
ECMAScript 6(es6)
[tcapulusdb knowledge base] tcapulusdb tmonitor module architecture introduction
File name setting causes an error to be written to writelines: oserror: [errno 22] invalid argument
go-zero微服务实战系列(七、请求量这么高该如何优化)
LeetCode 522 最长特殊序列II[枚举 双指针] HERODING的LeetCode之路
Brother sucks 590000 fans with his unique "quantum speed reading" skill: look at the street view for 0.1 seconds, and "snap" can be accurately found on the world map
闭包的常见问题
使用Karmada实现Helm应用的跨集群部署【云原生开源】
实验笔记之——CARMEN (.log .clf)文件转换为rosbag
Mail system (based on SMTP protocol and POP3 protocol -c language implementation)
R language plot visualization: plot to visualize the two-dimensional histogram contour map, add numerical labels on the contour lines, customize the label font color, and set the mouse hover display e
Evolution of software system architecture
[tcapulusdb knowledge base] Introduction to tmonitor stand-alone installation guidelines (I)
Privacy computing fat offline prediction
Error im002 when Oracle connects to MySQL