Xctf attack and defense world crypto master advanced area olddriver

1. Enter the environment , Download the attachment

This question is still very difficult for me , After watching it for two days, I can finally understand some ！ The attachment gives a enc.txt file , I opened it and took a look ,n and c It's big , and e Smaller and fixed , Conjecture and rsa of , After watching wp Just know is Low encryption index broadcast attack

Check out related blogs , What is a low encryption index broadcast attack ？

• Encryption index e A very small
• A clear text uses different modules n, The same encryption index e Encrypt multiple times
• You can get each encrypted ciphertext and the corresponding module n、 Encryption index e
• It can be obtained according to the Chinese surplus theorem m^e, Finally get the plaintext

2. Problem analysis

1. Their thinking
   Refer to the link of the boss https://www.cnblogs.com/lingxuer/p/15018183.html

• Observe the attachment , Found to have e,n,c Three parameter names , Consider that this topic will involve RSA
• Observe the attachment , be-all e Are the same value , And the value is not very large
• This topic may be written in clear text m Through multiple public keys (n,e) Encrypt and get multiple ciphertexts n
• Consider using low encryption index broadcast attack to obtain plaintext
• By judgment , All the ciphertext n Homocoprime , Use the Chinese Remainder Theorem to solve
• Turn the obtained value on e Power , The obtained value is converted to 16 Hexadecimal pass base16 Transform to get flag

2. What is the Chinese remainder theorem ？

• Reference link Introduction to Chinese remainder theorem
• Baidu Encyclopedia about the calculation of remainder theorem Sun Tzu's Theorem

The core of this problem is the result of solving the remainder theorem , Decrypt with the result , Then first imitate and write a code of remainder theorem ：

import gmpy2


def crt(b, m):
    #  Judge whether they are mutually prime 
    for i in range(len(m) - 1):
        for j in range(i + 1, len(m)):
            #  perhaps math.gcd() It's fine too 
            if gmpy2.gcd(m[i], m[j]) != 1:
                print(' There are non coprime numbers in modulus ！')
                return -1

    #  Product calculation 
    M = 1
    for i in range(len(m)):
        M *= m[i]

    Mm = []
    #  Mod  M/m[i]
    for i in range(len(m)):
        Mm.append(M // m[i])

    #  seek Mm[i] Multiplicative inverse element of 
    Mm_ = []
    for i in range(len(m)):
        t, a, _ = gmpy2.gcdext(Mm[i], m[i])
        Mm_.append(int(a % m[i]))

    #  Sum of 
    y = 0
    for i in range(len(m)):
        y += (Mm[i] * Mm_[i] * b[i])
    y = y % M
    return y
   
r = crt(b = [2, 3, 2], m = [3, 5, 7])

3. utilize n and c Solve with the remainder theorem function
   The code is as follows ：

from Crypto.Util.number import long_to_bytes


cip_keys = [
    {
    
        "c": 7366067574741171461722065133242916080495505913663250330082747465383676893970411476550748394841437418105312353971095003424322679616940371123028982189502042,
        "e": 10,
        "n": 25162507052339714421839688873734596177751124036723831003300959761137811490715205742941738406548150240861779301784133652165908227917415483137585388986274803},
    {
    
        "c": 21962825323300469151795920289886886562790942771546858500842179806566435767103803978885148772139305484319688249368999503784441507383476095946258011317951461,
        "e": 10,
        "n": 23976859589904419798320812097681858652325473791891232710431997202897819580634937070900625213218095330766877190212418023297341732808839488308551126409983193},
    {
    
        "c": 6569689420274066957835983390583585286570087619048110141187700584193792695235405077811544355169290382357149374107076406086154103351897890793598997687053983,
        "e": 10,
        "n": 18503782836858540043974558035601654610948915505645219820150251062305120148745545906567548650191832090823482852604346478335353784501076761922605361848703623},
    {
    
        "c": 4508246168044513518452493882713536390636741541551805821790338973797615971271867248584379813114125478195284692695928668946553625483179633266057122967547052,
        "e": 10,
        "n": 23383087478545512218713157932934746110721706819077423418060220083657713428503582801909807142802647367994289775015595100541168367083097506193809451365010723},
    {
    
        "c": 22966105670291282335588843018244161552764486373117942865966904076191122337435542553276743938817686729554714315494818922753880198945897222422137268427611672,
        "e": 10,
        "n": 31775649089861428671057909076144152870796722528112580479442073365053916012507273433028451755436987054722496057749731758475958301164082755003195632005308493},
    {
    
        "c": 17963313063405045742968136916219838352135561785389534381262979264585397896844470879023686508540355160998533122970239261072020689217153126649390825646712087,
        "e": 10,
        "n": 22246342022943432820696190444155665289928378653841172632283227888174495402248633061010615572642126584591103750338919213945646074833823905521643025879053949},
    {
    
        "c": 1652417534709029450380570653973705320986117679597563873022683140800507482560482948310131540948227797045505390333146191586749269249548168247316404074014639,
        "e": 10,
        "n": 25395461142670631268156106136028325744393358436617528677967249347353524924655001151849544022201772500033280822372661344352607434738696051779095736547813043},
    {
    
        "c": 15585771734488351039456631394040497759568679429510619219766191780807675361741859290490732451112648776648126779759368428205194684721516497026290981786239352,
        "e": 10,
        "n": 32056508892744184901289413287728039891303832311548608141088227876326753674154124775132776928481935378184756756785107540781632570295330486738268173167809047},
    {
    
        "c": 8965123421637694050044216844523379163347478029124815032832813225050732558524239660648746284884140746788823681886010577342254841014594570067467905682359797,
        "e": 10,
        "n": 52849766269541827474228189428820648574162539595985395992261649809907435742263020551050064268890333392877173572811691599841253150460219986817964461970736553},
    {
    
        "c": 13560945756543023008529388108446940847137853038437095244573035888531288577370829065666320069397898394848484847030321018915638381833935580958342719988978247,
        "e": 10,
        "n": 30415984800307578932946399987559088968355638354344823359397204419191241802721772499486615661699080998502439901585573950889047918537906687840725005496238621}
]

cips = []
keys = []

for cip_key in cip_keys:
    cips.append(cip_key['c'])
    keys.append(cip_key['n'])

r = crt(cips, keys)

res, _ = gmpy2.iroot(r, 10)
print(res)

print(long_to_bytes(res).decode())

Get the final result ：flag{wo0_th3_tr4in_i5_leav1ng_g3t_on_it}

4. Review again RSA The process
   
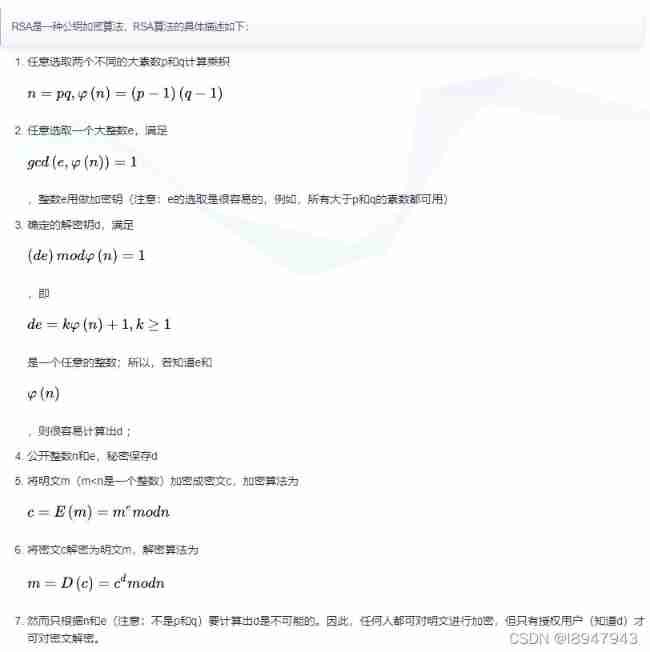
   knowledge has no limit , Damn it ！！！