Quick sorting (quick sorting) (implemented in C language)

Welcome to my 【 data structure 】 special column

• I am a Brant_zero, A student C/C++ Of college students .
• ️ My blog home page ​​​​​​Brant_zero The home page of
• Welcome your attention , Your attention is the biggest driving force of my creation

Preface

         The learning content of this blog is quick sorting , Quicksort has many different versions and optimizations , Our goal this time is to understand these versions , I don't say much nonsense , We began to .

        Length is longer than the , It is recommended to browse with the directory .

Catalog

One 、 Quick introduction and ideas

Two 、hoare edition

2.1 Single trip

2.2 Multiple processes

2.3 Implementation of multiple trips

3、 ... and 、 Excavation method

Four 、 Front and back pointer method

5、 ... and 、 Fast platoon optimization

5.1 The best of three key

5.2 Inter community transformation

6、 ... and 、 Quick sort to non recursive version

---

One 、 Quick introduction and ideas

Quick sort is C.R.A.Hoare On 1962 A partition exchange sort proposed in . It uses a divide and conquer strategy , It's often called divide and conquer .

The basic idea ：

• 1． Take a number from the sequence as the reference number first .
• 2． Partition process , Put all the larger numbers to the right of it , Less than or equal to its number all put it to the left .
• 3． Repeat the second step for the left and right sections , Until there is only one number in each interval .

---

Two 、hoare edition

2.1 Single trip

hoare Version is the quickest and most original version , Let's take a look at the following GIF Let's take a look at the exchange process of a single trip .

Single trip ：

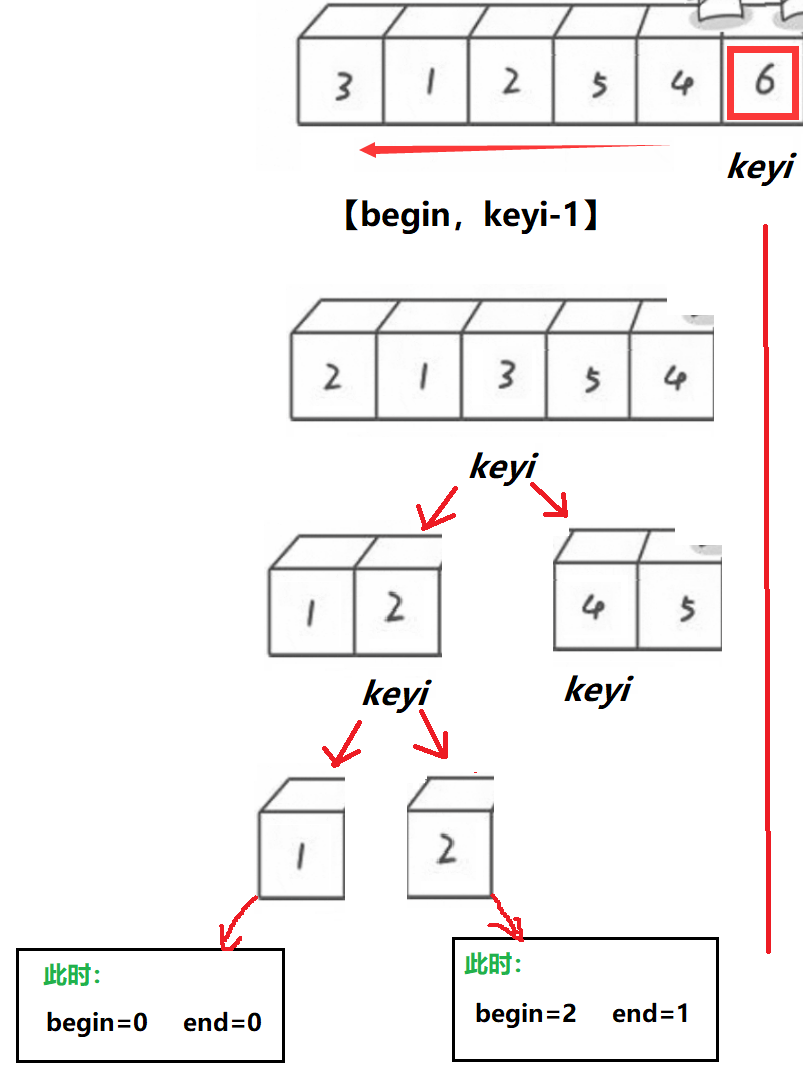
1.   First record keyi Location , then left and right Start at both ends of the array and go to the middle .
2. right First Start moving in the middle , If right The value at is less than keyi Place the value of the , Then stop waiting left go .
3. left Taking action , When left You can find keyi At a small value ,left and right Exchange the values at .
4. When two positions meet , Compare the value of the encounter position with keyi Exchange the values at , And set the meeting position as new keyi.

Let's take a look at the following code , Then analyze the errors that are easy to occur .

    // Single trip ：
	// First keyi Record begin Data at 
	int keyi = begin;
	int left = begin;
	int right = end;
	// The two pointers begin to move towards the middle 
	while (left < right)
	{
		//right Act first , Be sure to find   Greater than  keyi The value of the location 
		while(left < right && a[right] >= a[keyi])
		{
			right--;
		}
		//left action , Be sure to find   Less than  keyi The value of the location 
		while (left < right && a[left] <= a[keyi])
		{
			left++;
		}
		// Reach the specified location , swapping 
		swap(&a[left], &a[right]);
	}
	// After the above steps , Two subscripts will converge in one place 
	// Then exchange the values of these two positions 
	swap(&a[right], &a[keyi]);
	keyi = right;
	//[begin,keyi-1],keyi,[keyi+1],end

It's easy to get wrong ：

1. If keyi The leftmost data recorded , Then let right The pointer acts first , Because of this We must ensure that the place where we meet is better than keyi The value at is smaller . The meeting place is R Where to stop , The good news is right The value ratio of keiy Small place , The worst case scenario is right Go to the keyi The location of , At this time, the exchange is bad and has no effect .
2. When finding value ,left or right Place the value of the A certain than keyi Situated Small ( Big ), It's no good , If the following situations occur, there will be an endless cycle .
3. stay left and right Judge when looking for the value in the middle left<right, If you don't control ,left or right It's easy to get out of the array .

2.2 Multiple processes

After the single trip above , We will find that ,keyi All on the left are less than a[keyi] Of , All on the right are greater than a[keyi] Of .

Then we keep repeating the sequence of this single trip , You can sort the entire array , This is typically a Recursive divide and conquer Thought .

The basic idea ：

1. take keyi Divided into two sides , Recursion separately , Similar to the preorder traversal of binary tree .
2. Divided into [begin,keyi-1],  keyi,   [keyi+1,end].
3. Recursion end condition ： When begin == end  Or is it Array error (begin>end) when , Is the end condition .

2.3 Implementation of multiple trips

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	// The realization of one trip 
	int left = begin;
	int right = end;
	int keyi = left;
	while (left < right)
	{
		// Start moving on the right     Must add equal , Because quick sort is looking for a value that must be smaller than it 
		while (left < right && a[keyi] <= a[right])
		{
			right--;
		}
		// Start moving on the left 
		while (left < right &&   a[left] <= a[keyi])
		{
			left++;
		}
		swap(&a[left], &a[right]);

	}
	swap(&(a[keyi]), &(a[right]));
	keyi = right;
	//[begin,keyi-1] keyi [keyi+1,end]
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi+1, end);
}

Effect test ：

---

3、 ... and 、 Excavation method

Presumably, there are still people who are right hoare In the version , Why is the left set to keyi You have to go first on the right. You can't understand , Someone here has come up with a new version of fast platoon , Although the algorithm is the same , But it is more conducive to understanding .

secondly , These two methods have different results in a single trip , This leads to different results for fast single trip scheduling on some topics , So let's understand the algorithm idea of this digging method .

Let's take a look at the following animation ：

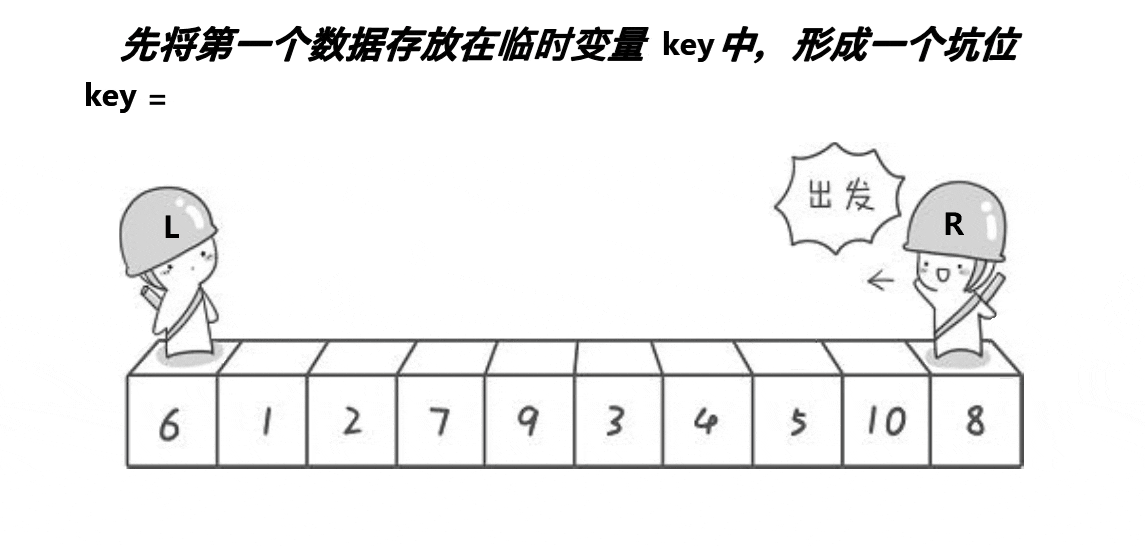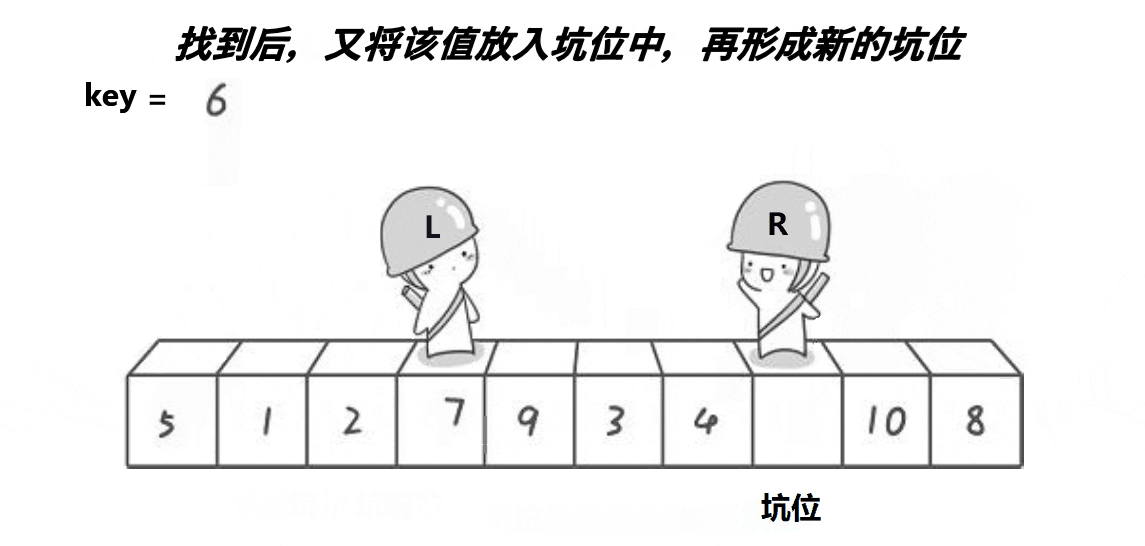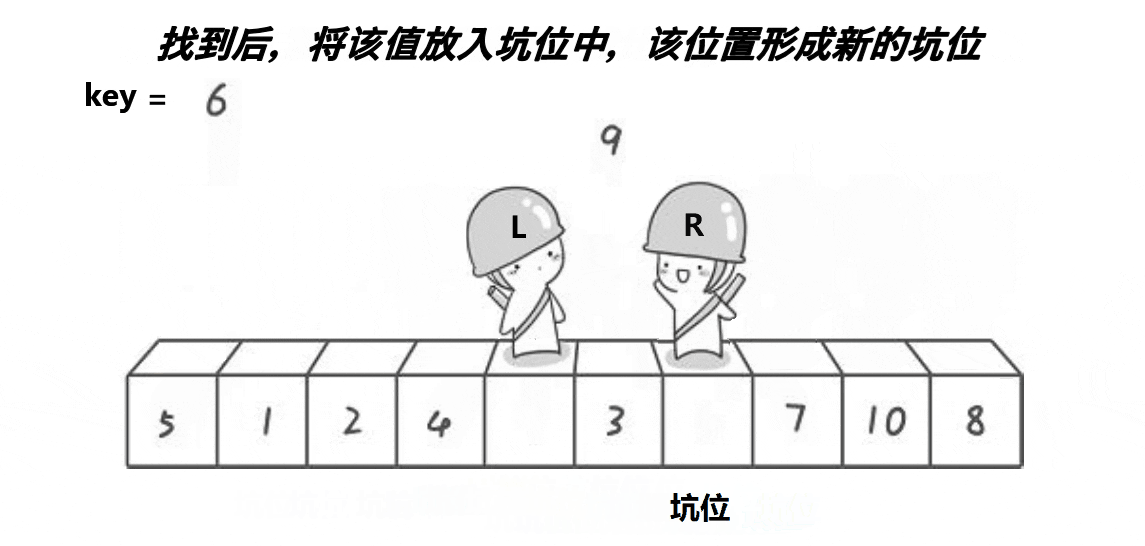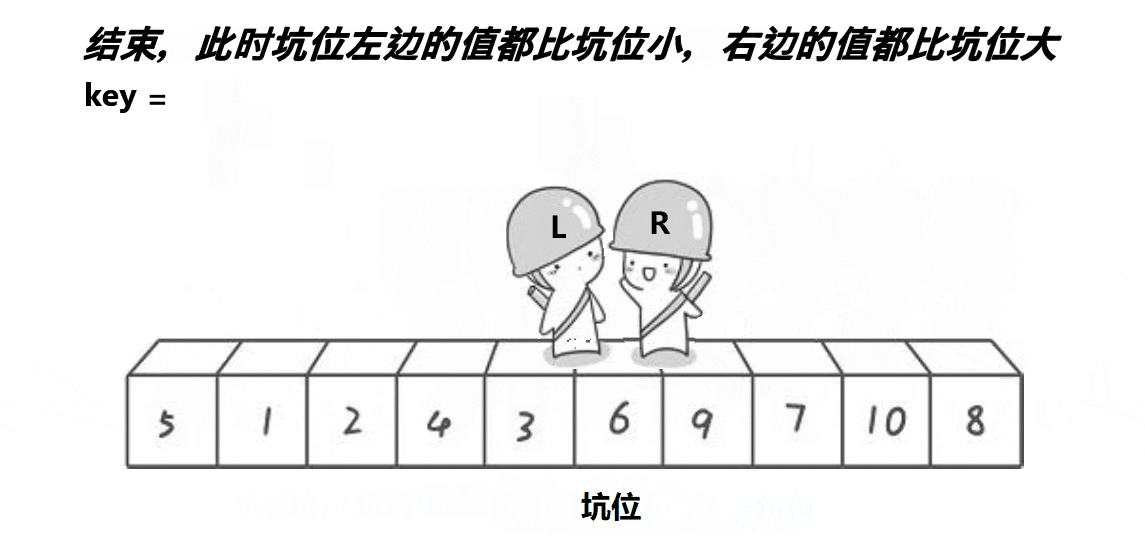
Algorithm ideas ：

1. take begin Place the value at key in , Put it in the pit (pit), then right Start looking for value to fill the hole .
2. right Find the ratio key Put the value into the pit after the small value , Then put here Set it as a new pit .
3. left Also action began to find value to fill the hole , Find the ratio key Large values put it into the pit , Set it as a new pit .
4. When left And right When we met , take key Put it into the pit in .
5. Then proceed [begin,piti-1],  piti,   [piti+1,end] Recursive divide and conquer of .

Because of the hoare Implementation of version , So I won't repeat it here , The above algorithm idea has clearly described the process .

// Quick line up    Excavation method 
void QuickSort_dig(int* a, int begin, int end)
{
	if (begin >= end)
		return;
	// The realization of one trip 
	int key = a[begin];
	int piti = begin;
	int left = begin;
	int right = end;
		while (left < right)
		{
			while (left < right && a[right] >= key)
			{
				right--;
			}
			a[piti] = a[right];
			piti = right;
			while (left < right && a[left] <= key)
			{
				left++;
			}
			a[piti] = a[left];
			piti = left;
		}
		// Mend a hole 
		a[piti] = key;
	//[begin, piti - 1] piti [piti + 1, end]
	QuickSort_dig(a, begin, piti - 1);
	QuickSort_dig(a, piti + 1, end);
}

  Effect test ：

---

Four 、 Front and back pointer method

The front and back pointer method is compared with hoare And excavation , Both the algorithm idea and the implementation process have been greatly improved , It is also a mainstream way of writing , Here, let's take a look at the process of a single trip .

Algorithm ideas ：

1. cur be located begin+1 The location of ,prev be located begin Location ,keyi Store first begin Place the value of the .
2. cur Keep moving forward +1, until cur >= end Stop the cycle when .
3. If cur The value at is less than key Place the value of the , also prev+1 != cur, Then with prev Exchange the values at .
4. When the loop ends , take prev The value at is the same as keyi The values of are exchanged , And set it as new keyi Location .

Code implementation ：

void QuickSort_Pointer(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	// The data range is large and 10, quicksort 
    int prev = begin;
	int cur = begin + 1;
	int keyi = begin;
	// Right after the middle of three numbers keyi The value of the position is exchanged 
	int mid = GetMid(a, begin, end);
	swap(&a[mid], &a[keyi]);
	while (cur <= end)
	{
		//cur Go straight ahead , If you encounter less than and prev++ It's not equal to cur The exchange ,
		// Because if prev+1 == cur  Then you will exchange with yourself 
		if (a[cur] < a[keyi] && ((++prev) != cur))
		{
			swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	swap(&a[prev], &a[keyi]);
	keyi = prev;
	// Start recursion 
	QuickSort_Pointer(a, begin, keyi - 1);
	QuickSort_Pointer(a, keyi + 1, end);
}

Be careful ：

1. In the process of traversal ,cur Is constantly moving forward , It's just cur The value at is less than keyi At the value of , Just need to exchange and judge .
2. stay cur The value at position is less than keyi At the value of , To judge prev++ Is it equal to cur, If it is equal to , Then you will exchange with yourself . If equal , No exchange .

5、 ... and 、 Fast platoon optimization

5.1 The best of three key

After implementing quick sorting , We found that ,keyi The location of , It is a major factor affecting the efficiency of quick sorting . Therefore, someone has adopted the method of taking three numbers to solve the problem of choosing keyi Inappropriate questions .

Take the three Numbers

That is to know the beginning and end of this set of disordered sequence , We just need to be first , in , Of the last three data , Select a data in the middle as the benchmark (keyi), quicksort , It can further improve the efficiency of quick sorting .

// Take the three Numbers 
int GetMid(int *a,int begin, int end)
{
	int mid = (begin + end) / 2;
	if (a[begin] > a[end])
	{
		if (a[end] > a[mid])
			return end;
		else if (a[mid] > a[begin])
			return begin;
		else
			return mid;
	}
	else
	{
		if (a[end] < a[mid])
			return end;
		else if (a[end] < a[begin])
			return begin;
		else
			return mid;
	}
}

  such , The subscript of the intermediate value is returned , Then we change this position to a new one keyi, That's all right. .

5.2 Inter community transformation

Because quick sort is recursive , When recursive to the last few layers , At this time, the values in the array are actually close to order , Moreover, recursion of this interval will greatly occupy the stack ( Where the function stack frame is opened ) Space ,

Next , We optimize it , If the amount of interval data is less than 10, We won't do recursive quick sort , Instead, use insert sort .

Let's take a look at the fast platoon after using inter cell transformation optimization and triple data extraction optimization .

void QuickSort_Pointer(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	// The data range is large and 10, quicksort 
	if (end - begin > 10)
	{
		int prev = begin;
		int cur = begin + 1;
		int keyi = begin;
		// Right after the middle of three numbers keyi The value of the position is exchanged 
		int mid = GetMid(a, begin, end);
		swap(&a[mid], &a[keyi]);
		while (cur <= end)
		{
			if (a[cur] < a[keyi] && ((++prev) != cur))
			{
				swap(&a[cur], &a[prev]);
			}
			cur++;
		}
		swap(&a[prev], &a[keyi]);
		keyi = prev;
		// Start recursion 
		QuickSort_Pointer(a, begin, keyi - 1);
		QuickSort_Pointer(a, keyi + 1, end);
	}
	else
	{
		// Left and right closed 
		InsertSort(a, end - begin + 1);
		InsertSort(a + begin, end - begin + 1);
	}

}

Be careful ：

1. Insert two parameters after sorting , One is the starting address of the data set , The second is the amount of data .
2. When using insert sort , We need to pass in the actual address of the data set to be sorted , namely a+begin, If the incoming is a, That sort is always array a Before n Intervals .
3. The number of data passed in by insert sort , So we're going to end-begin add 1 Then it is transferred . Quick sort end、begin They're all closed intervals ( That is, array subscript ).

6、 ... and 、 Quick sort to non recursive version

Because the function stack frame is on the stack ( Stack on non data structure ) It's opened up on the Internet , Therefore, stack overflow is easy to occur , To solve this problem , In addition to the above two optimizations , You can also change the quick sort to a non recursive version , In this way, the development of space is on the heap , There is much more space on the heap than on the stack .

In order to achieve a non recursive version of quicksort , We need to use the stack we implemented before , To simulate non recursive .

Realize the idea ：

1. Be sure to enter the stack first on the left and then on the right .
2. Take the element at the top of the stack twice , Then sort in a single pass .
3. Divided into [left , keyi - 1] keyi [ keyi +  1 , right ] Right 、 Stack left .
4. loop 2、3 Step until the stack is empty .

int PartSort(int * a, int begin, int end)
{
	int prev = begin;
	int cur = begin + 1;
	int keyi = begin;
	int mid = GetMid(a, begin, end);
	swap(&a[mid], &a[keyi]);
	while (cur <= end)
	{
		if (a[cur] < a[keyi] && ((++prev) != cur))
		{
			swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	swap(&a[prev], &a[keyi]);
	return prev;
}
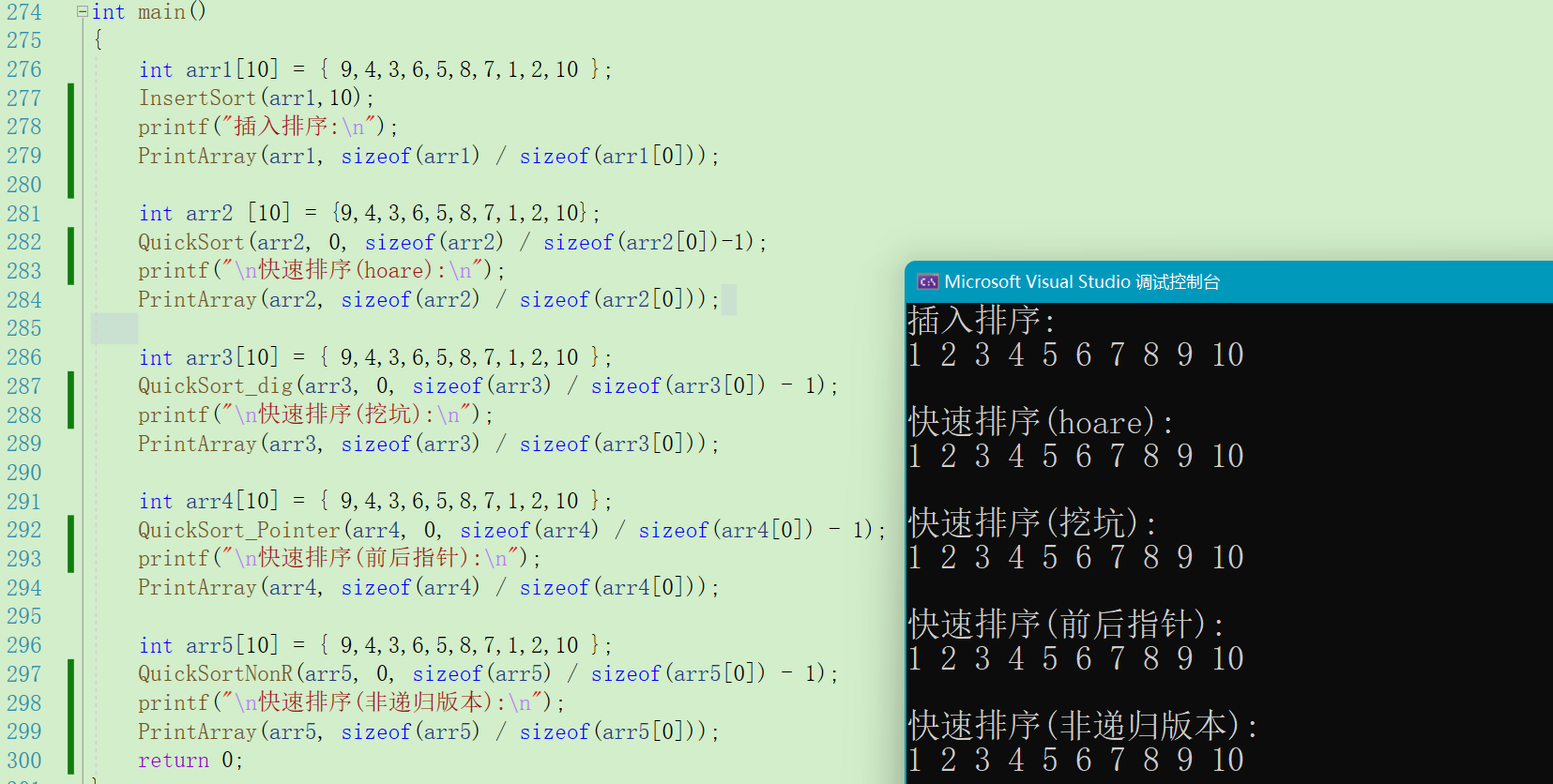
void QuickSortNonR(int* a, int begin, int end)
{
	ST st;
	StackInit(&st);
	// First on the right   Reentry left 
	StackPush(&st, end);
	StackPush(&st, begin);
	while (!StackEmpty(&st))
	{
		// Out of the stack   It is left first and then right 
		int left = StackTop(&st);
		StackPop(&st);
		int right = StackTop(&st);
		StackPop(&st);
		int keyi = PartSort(a, left, right);
		//[left, keyi - 1] keyi[keyi + 1, right];
		// The interval in the stack    Will be sorted and divided in a single run 

		if (keyi + 1 < right)// It shows that there are at least two data 
		{
			// Go right then left 
			// To ensure that when taken out   The order is the same 
			StackPush(&st, right);
			StackPush(&st, keyi + 1);
		}
		// If it is less than , Explain that there are at least two more elements   To be sorted 
		if (left < keyi - 1)
		{
			// Go right then left 
			StackPush(&st, keyi - 1);
			StackPush(&st, left);
		}
	}
	StackDestory(&st);
}

Effect demonstration ：

---

summary

This article introduces hoare Law 、 Excavation method 、 Front and back pointer method , And two optimization methods of fast scheduling and non recursive version , It's still very difficult , Check the dynamic diagram when you realize , Then try to write an order by yourself , Then combine the content of the blog to understand the idea of fast recursion . The content of this article is relatively hard core , It's hard to understand just by looking , Especially contact hoare Version and non recursive version , I hope you can cooperate in debugging 、 Draw a picture to realize .

well , This blog is over , The next blog will update the relevant content of merging and sorting , I hope you will continue to pay attention , If you can, point a free like or follow , Your feedback is my biggest motivation to update .