Another way of understanding the essence of Hamming code

---

Preface

It has been a long time since we learned computer composition , The forgotten Savior is coming , I read Haiming code in the process of Review , At that time, I knew a little about Haiming code , Review again, although you can solve problems , But I can't understand its principle ： Why can we correct , Why can we detect errors , After thinking for a long time, I got nothing , In a trance, I thought of a way of understanding , So it was recorded , I won't go into details about Haiming code .

One 、 The distance between string and binary string

In this article, we only discuss the distance of strings with the same length . The distance between strings with the same length refers to modifying characters at least times and trying to make two strings equal , for example “ABC“ and ”ABD“ A distance of 1,”ABCD“ and ”ABBB“ A distance of 2. Similarly, when the characters are only ‘0’ and ‘1’ when , You can define the distance between binary strings , Such as
1000 and 1001 The distance to 1,1111 and 0000 The distance to 4, The distance here is not a numerical difference

Two 、 Hamming code is just a series of processed data

Hamming code contains original data , But we always ignore that Hamming code itself is also a kind of data , Hamming code and source code have many to one mapping relationship .

Two 、 analysis

Distance of binary string and undirected graph

Briefly analyze the distance of a set of binary strings , Set the length to K Binary string of , Let's know that the distance between them is 1 The binary string of is K individual , for example 000 There are three strings with a distance of one ：100、010,001. The maximum distance between two binary strings is K, For example, 0000 The biggest distance is 1111.

Since there is a distance , I have to think of pictures , As you can imagine , A binary string is a dot , A distance of 1 The strings of are directly connected ： such as 3 The graph of the graph corresponding to the bit binary string ：

（ No, cad Use window Draw a picture , Although only the topology of the graph does not specify the definite style , But I still paint it as a cube ）
At this time, we can say that a jump is to move from a point on the graph to another nearby point , such as :
001---->101;
For ordinary odd or even parity check , Have an error detection ability , If we also want to implement in this graph or cube , Then the distance from the effective point is 1 All points of are invalid points , Such points can be found casually 4 individual ：001,010,100,111, These four points can be used to represent the effective value , Any bit error can be detected ,（ This is the last code of odd number validation ）, Map... Separately 1,2,3,4, Of course, if you like , It can be mapped to any four different values

At this time, we think about coding with one bit error correction ability , Suppose that an error free binary string is called the center point , A wrong point is that the distance between the center points is 1 The point of , Call it effective , Then the effective point and the center point represent the same data , So presumably , The central point is always surrounded by the effective point , The distance between the two centers is at least 3. Find the distance in this cube is 2 Two points of , You can know that these are the two farthest endpoints , for example {000,111},{001,110} etc. , We know {001} and {111}, It's three Hamming codes without total validation code , When there is an error, you can still know the correct value .

Read here , I believe you have roughly understood this idea , Coding with error correction capability , Completely correct coding is like a lighthouse ,, When moving not too far away （ Move a bit ）, Can still walk back to the right lighthouse , If you go too far （ That is, there are twoorthree bit errors ） Go to the light of other lighthouses , At this time, no mistakes can be found , For codes with error detection capability , Error codes are like black areas without light , It is impossible to find the right lighthouse （ The value of the original ）, But I can know that something wrong happened .

If the length of the binary string is K, I hope to encode a code so that it can correct one digit , Then there are K Effective points ,K+1 Points represent a value , Altogether 2^ K A little bit , Then it can store at most n= 2^K/（1+k） Data , When K=3,n=2;K=7,n=2 ^5, That's exactly what it is. 3 Bit and 7 The data size that bit Hamming code can store , about K!= 2 ^i-1（i=1,2,3,4） Value , Presumably a little wasteful . There are invalid points , Invalid points = All points - Center point - Effective points .
Although mathematics is not good, it is impossible to deduce how many central points there are , But it can be inferred through Hamming code , The data bits of Hamming code have
$$K-\lfloor {\log }_{2}K\rfloor -1$$
Then the central point is
$$2^{K-\lfloor {\log }_{2}K\rfloor -1}$$
The effective points are
$$K\ast 2^{K-\lfloor {\log }_{2}K\rfloor -1}$$
Invalid points are
$$2^K-2^{K-\lfloor {\log }_{2}K\rfloor -1}-K\ast 2^{K-\lfloor {\log }_{2}K\rfloor -1}$$
When K=2^i-1（i=1,2,3,…） Time invalid point ：
$$2^{2^i-1}-2^{2^i-1-\lfloor {\log }_2{2}^i-1\rfloor -1}-(2^i-1)\ast 2^{2^i-1-\lfloor {\log }_2{2}^i-1\rfloor -1}$$
$$2^{2^i-1}-2^{2^i-i-1}-(2^i-1)\ast 2^{2^i-i-1}$$
$$2^{2^i-1}-2^{2^i-i-1}-(2^i\ast 2^{2^i-i-1}+\ast 2^{2^i-i-1})$$
$$0$$
So Dangdang K=2^i-1（i=1,2,3,…） Time efficiency is the highest, and there is no invalid point , Although it is deduced from Hamming code , But it can be believed that if a big man can calculate the number of central points from the figure, it should also be the same .

In this way, other error correction and detection codes are also similar , If you want two correction , It is necessary to find a distance of 5 The point of . because K At least for 5 There can be two points , We can 00000 representative 0, take 11111 representative 1, Then this coding two bit error can still be corrected , Of course, there are many points like this , such as 11110,00001, It doesn't matter what value it maps to , Data can be stored as long as there are multiple states .

3、 ... and , The successor of binary string graph

Bit length of binary string K,K=1 Diagram of time binary string （ Don't mark the value ）
K=2

K=3
K=4.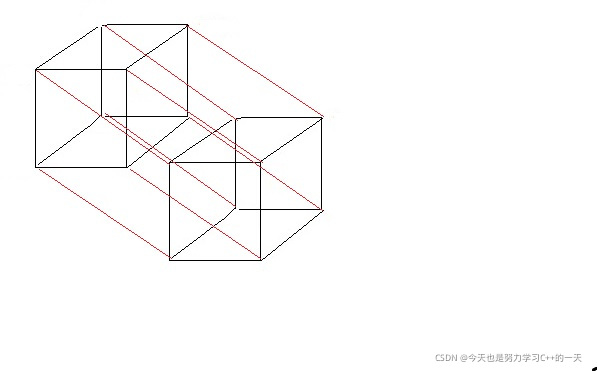
It can be seen that , about K+1 The figure of bit is K The graph of bits is copied and the copied points are connected , Because binary string x1,x2,x3…1 and x1,x2,x3…0（xi=0 or 1,i=1,2,3…） The distance is always 1. about K=4, We cannot find three pairwise distances greater than or equal to 3 The point of , therefore 4 Bit Hamming code can only store 1 A data ,

If you put K As a dimension , Maybe it can simulate a beautiful model , Or lay all the points on a sphere , As you can imagine , Because every point has K The adjacent point of , The distribution of these points is uniform and symmetrical , to want to 1 Bit error correction , Find a point on the ball with a distance of more than or equal to two 3 The center of , to want to 1 Bit error correction , You two check the error , Find a point on the ball with a distance of more than or equal to two 4 The point of , The distance from each center point is 2 The point of is invalid , If it works CG Make animation to find some 、 Error detection 、 The process of error correction , And center point 、 Effective point 、 Invalid dots are made into different colors , Then we can more intuitively understand the deep principle of Hamming code , I hope interested and capable bosses can make it .
（ Level co., LTD. , Please point out the mistake ）.