Machine learning 6-decision tree

One . Decision tree Overview

1.1 What is a decision tree

Decision tree input : Test set
Decision tree output : Classification rules ( Decision tree )

1.2 Overview of decision tree algorithm

Several common examples of decision trees

1. ID3 Decision tree
2. C4.5 Decision tree
3. CART classification （ Return to ） Trees

Maximum gain of variable information , Is the most important variable , Put it on the top
There are many values for variables , But it is limited in the training set , So it can be marked

Age	Separation point	Whether the information gain is maximum
12
18	15
19	18.5
22	20.5	yes
29	25.5
40	34.5
If 20.5 It's about , Maximum information gain , Then this is the best separation point

Two . Construction of a decision tree

2.1 Construction of a decision tree ： Divide and rule （divide and conquer）

Decision tree is a typical model with local and global similarity , That is, in any path , Any internal node forms a root node “ Sub decision tree ”. For such a model , Efficient 、 The feasible construction method is divide and conquer . Steps are as follows ：
Input ： Data sets $D=(x_1,y_1),(x_2,y_2),..,(x_m,y_m)$ And its characteristic space $A=a_1,a_2,\dots ,a_d$
function TreeGenerate(D,A)

1. Generate the nodes Node
2. If the dataset D All belong to a certain category C, Will 1 The nodes in the Node Divided into attributes C, return
3. If A For an empty set , perhaps D stay A The values on are exactly the same , be 1 The nodes in the Node Mark as leaf node , The category is D Most of the categories in , return
4. Select the optimal splitting node a,
   For each value $a^V$ in a:
   From the node Node Generate a branch , Make the data set 𝐷_𝑉 yes D stay a The value in is $a^V$ Subset
   if 𝐷_𝑉 It's an empty set , Then the branch is used as a leaf node , The category is D Most of the categories in , return ;else Generate branch TreeGenerate(𝐷_𝑉, A{a})
   End for

This is a typical recursive process , The return condition is ：

1. The current node contains samples of the same category
2. The current property is empty
3. All attribute values are the same
4. The sample set contained in the current node is empty

The output of the leaf node ：
The category with the largest proportion of leaf node output , That is, the category with the highest output probability . If it is transformed to output the corresponding probability of each category , It can be used to calculate the output probability in random forest .

Two questions ： How to select the optimal attribute ？ How to split nodes ？
The choice of optimal attributes

1. Information gain and information gain rate
2. gini index
   Split node
3. discrete , There are few types of values
4. discrete , There are many types of values
5. Continuous type

2.2 Information gain （Information Gain）

The information entropy that measures the purity of categories ：
Suppose the sample D pass the civil examinations k The proportion of class samples is $p_K$, be D The entropy of information is defined as
$$Entropy(D)=-\sum _k{p}_{k}lo{g}_2{p}_k$$
Entropy The smaller it is , The higher the purity

Information entropy ：entropy It represents the uncertainty of information In other words, the degree of chaos of the data , Take loans for example ,2 Person overdue ,2 People are the most chaotic when they are not overdue , The uncertainty is the highest , Information entropy is the maximum . The purity is the lowest .

Information gain ：
if D By attribute a Divide into $D={\bigcup }_v{D}_v,D_v\cap D_w=\varnothing$, Define the information gain as ：
$$Gain(D,a)=Entropy(D)-\sum _v\frac{|D_v|}{|D|}Entropy(D_v)$$

Now we have a data set D（ For example, loan information registration form ） And characteristics A（ For example, age ）, be A The information gain is D Entropy and characteristics of itself A Given the conditions D The difference of conditional entropy , namely ：
$$g(D,A)=H(D)-H(D|A)$$
Data sets D The entropy of is a constant . The larger the information gain , I mean conditional entropy The smaller it is ,A eliminate D The greater the credit for the uncertainty .

Therefore, features with large information gain shall be preferred , They have a stronger ability to classify . This generates a decision tree , be called ID3 Algorithm .

The role and characteristics of information gain ：

1. Measure the degree of change from disorder to order （ Commonly used in ID3 Decision tree ）
2. Select the attribute with the maximum information gain to split
3. No generalization ability , Have a preference for attributes with more values
   To control the influence of the number of attribute values , First define IV：
   $$IV(a)=-\sum _v\frac{|D_v|}{|D|}lo{g}_2\frac{|D_v|}{|D|}$$

2.3 Information gain rate

When a feature has multiple candidate values , Information gain tends to be too large , Cause error . This problem can be corrected by introducing information gain rate .
Information gain rate is information gain and data set D Entropy ratio of ：
$$GainRatio=\frac{Gain(D,a)}{IV(a)}$$

characteristic ：
It is easy to tend to attribute with few values
The attribute with the maximum gain rate can be selected for splitting
You can select an attribute set that is greater than the average gain rate , Then select the attribute with the lowest gain rate

2.4 gini index

Another measure of purity
$$Gini(D)=1-\sum _k{p}_k^2$$
Gini The smaller it is , The higher the purity
attribute a In the data set D The Gini index in is
$$Gini(D,a)=\sum _v\frac{|D_v|}{|D|}Gini(D_v)$$
Select the attribute with the minimum Gini index , namely $a_{\ast }=argminGini(D,a)$

2.5 Example

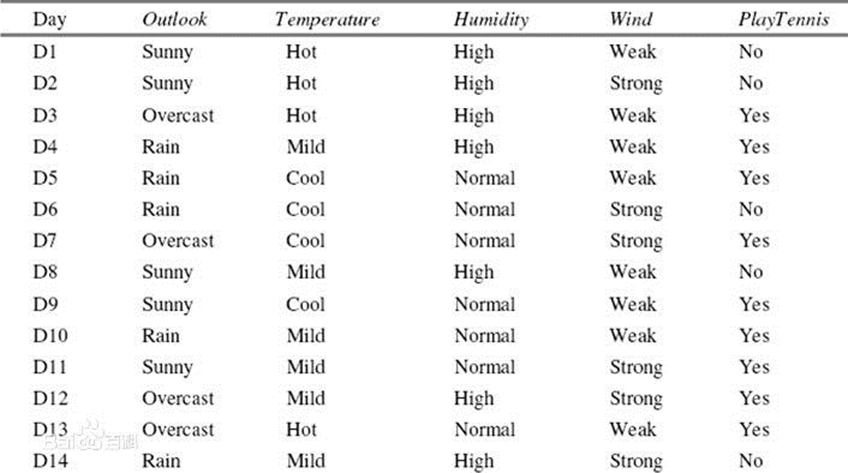
A simple example ： With variable outlook,temperature,humidity,wind Come on playtennis To classify .

about outlook, Its information gain rate is calculated as ：
（1） The calculation of the total entropy ：
P(PlayTennis=Yes) = 9/14, P(PlayTennis=No) = 5/14
Entropy = -9/14*log2(9/14) – 5/14*log2(5/14) =0.9403
（2） Put the dataset D according to Outlook division , The result is ：
D1: Outlook=Sunny Yes 5 Samples , among PlayTennis=Yes Yes 2 Samples ,PlayTennis=No Yes 3 Samples
Entropy1 = -2/5*log2(2/5)-3/5*log2(3/5) =0.9710
D2: Outlook=Overcast Yes 4 Samples , among PlayTennis=Yes Yes 4 Samples ,PlayTennis=No Yes 0 Samples
Entropy2 = -0/4*log2(0/4)-4/4*log2(4/4) =0 ( Definition 0*log2(0)=0)
D3: Outlook=Rain Yes 5 Samples , among PlayTennis=Yes Yes 3 Samples ,PlayTennis=No Yes 2 Samples
Entropy3 = -3/5*log2(3/5)-2/5*log2(2/5) = 0.9710
（3） Calculation IV： IV=-5/14*log2(5/14)-4/14*log2(4/14)-5/14*log2(5/14)= 1.5774
（4） Calculated information gain ：Gain = 0.9403-5/14* 0.9710-4/14*0-5/14* 0.9710= 0.2467
（5） Calculate the information gain rate ：Gain Ratio= 0.2467/ 1.5774= 0.1564

Calculation Outlook Of Gini：
（1） Calculation D1,D2 and D3 Of Gini：
Gini1 = 1-(2/5)^2-(3/5)2=0.4800,Gini2 = 1-(4/4)^2-(0/4)2=0
Gini3 = 1-(2/5)^2-(3/5)2=0.4800
（2） Calculate the total Gini:
Gini(D)=5/140.4800 + 4/140 + 5/15* 2=0.4800= 0.3086

2.6 Processing of continuous variables

Continuous variables are discretized by dichotomy , And then treat it as a discrete variable .

3、 ... and . Prevent fitting ： The art of pruning

There's a good chance , All attributes are split , Easy to create over fitting

Avoid overfitting , Need pruning (pruning). Two methods of pruning

1. pre-pruning
   In the process of decision tree generation , Each node is estimated before partition , If the current node partition can not improve the generalization performance of the decision tree , Then the partition is stopped and the current node is marked as a leaf node
2. After pruning
   First, a completed decision tree is generated from the training set , Then investigate the non leaf nodes from bottom to top , If the subtree corresponding to this node is replaced with leaf nodes, the generalization performance of the decision tree can be improved , Replace the subtree with a leaf node

** Generalization ability ：** The adaptability of the algorithm to fresh samples . You can use the set aside method , That is, select a part of the training set that does not participate in the construction of the decision tree , It is used to evaluate the test of a certain node partition or subtree merging .

Four . A combination method to improve the accuracy of classifiers

4.1 Overview of combination methods

Why combination method can improve classification accuracy

Advantages of combinatorial algorithms

4.2 Bagging algorithm

There's put back sampling :

Advantages of bagging algorithm :

4.3 promote (boosting) Algorithmic thought

Adaboost Algorithm :

Advantages and disadvantages of the lifting algorithm :

4.4 Random forests

Decision tree reinforcement algorithm : Random forests

4.4.1 The basic concept of random forest

Random forest is a kind of integrated model . It consists of several decision trees , The final judgment result is decided by simple voting based on the result of each decision tree .

4.4.2 Data set extraction

In the process of building a random forest model , The key step is to extract some samples from the original data set to form a new training set , And the sample size remains unchanged . The subsequent construction of each decision tree model is based on the corresponding sampling training set .
“ Random forests ” Medium “ Random ” The two characters are mainly reflected in 2 aspect ：

1. When extracting data from the overall training set , The sample is taken back .
2. After forming a new training set , And then extract some attributes from the attribute set without putting them back to develop the decision tree model

These random operations can enhance the generalization ability of the model , The problem of over fitting is effectively avoided . And other models （ For example, maximal gradient lifting tree ）.
stay 1 in , Every time a data set with the same sample size is generated by putting it back , There are about 1/3 The sample of is not selected , Reserved for “ Out of bag data ”
stay 2 in , Assuming the original m Attributes , In the 2 The general choice in this step is log_2⁡𝑚 Attribute for decision tree development .

4.4.3 Fusion of decision tree results

After getting several decision trees , Will fuse the results of the model . In random forests , The method of fusion is usually simple voting . hypothesis K The votes for each decision tree are 𝑡_1, 𝑡_2,…,𝑡_𝐾, 𝑡_𝑖∈{0,1}, The final classification result is

The output probability of random forest
At the same time, random forest also supports the output of results in the form of probability ：

Reference resources :

1. http://www.dataguru.cn/article-4063-1.html
2. https://zhuanlan.zhihu.com/p/76590801