不精确微分/不完全微分（Inexact differential/Imperfect differential）

---

不精确微分（inexact differential）或不完全微分（imperfect differential）是其积分取决于路径的微分。 它最常用于热力学中，表示热和功等路径相关量的变化，但在数学中更普遍地定义为一种微分形式。 相反，精确微分（exact differential/perfect differential，有时也称为 total differential/full differential，即全微分）的积分始终是路径无关的，因为积分的作用是反转微分算子（differential operator）。 因此，具有不精确微分的量不能表示为仅微分内变量（variables within the differential）的函数。 也就是说，它的值不能仅通过查看给定系统的初始状态和最终状态来推断。不精确微分主要用于涉及热和功的计算，因为它们是路径函数（path functions），而不是状态函数（state functions）。

1. 定义

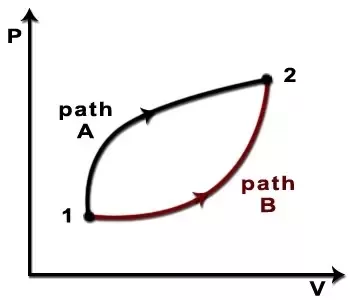
不精确微分 $\delta u$ 是在一些具有相同端点的两条路径上的积分不同的微分。具体来说，存在可积路径 ${\gamma }_1$，${\gamma }_2$：$[0,1]\to \mathbb{R}$ 使得 ${\gamma }_1(0)={\gamma }_2(0)$，${\gamma }_1(1)={\gamma }_2(1)$， 和

$${\int }_{{\gamma }_1}\delta u\ne {\int }_{{\gamma }_2}\delta u$$

在这种情况下，我们将积分分别表示为 $\Delta u{|}_{{\gamma }_1}$ 和 $\Delta u{|}_{{\gamma }_2}$ ，以明确我们正在考虑的量 $u$ 的变化的路径依赖性。

更一般地说，不精确微分 $\delta u$ 是一种微分形式，它不是精确微分，即对于所有函数 $f$，

$$\mathrm{d}f\ne \delta u$$

线积分的微积分基本定理（fundamental theorem of calculus for line integrals）需要路径独立性，以便用另一个函数的偏导数表示给定向量场的值，该函数是反导数的多元模拟。这是因为对于不精确的微分，不存在唯一的反导数表示，因为它们的变化在不同的路径上是不一致的。这种路径独立性的规定是对微积分基本定理的必要补充，因为在一维微积分中，函数定义的两点之间只有一条路径。

符号
热力学
使用符号 δ 代替微分符号 d，这一约定起源于 19 世纪德国数学家 Carl Gottfried Neumann 的著作，[2] 表明 Q（热）和 W（功）是路径相关的，而 U （内能）不是。

统计力学
在统计力学中，不精确的微分通常用通过微分算子 đ.[3] 的条形表示在 LaTeX 中，命令 “\rlap{\textrm{d}}{\bar{\phantom{w}}}” 是染料字符的近似值或简称为 “\dj”，它需要 T1 编码。

数学
在数学中，不精确微分通常只是更一般地称为微分形式，通常写为 {\displaystyle \omega }\omega 。 [4]

例子
总距离
当你从点 {\displaystyle A}A 沿着直线 {\displaystyle {\overline {AB}}}{\displaystyle {\overline {AB}}} 步行到点 {\displaystyle B}B）时（不改变方向) 你的净位移和总距离都等于所述线 {\displaystyle AB}{\displaystyle AB} 的长度。如果您随后返回点 {\displaystyle A}A（不改变方向），那么您的净位移为零，而您的总距离为 {\displaystyle 2AB}{\displaystyle 2AB}。这个例子抓住了一维不精确微分背后的基本思想。请注意，如果我们允许自己改变方向，那么我们可以在从 {\displaystyle A}A 到 {\displaystyle B}B 的任何时间点向前走一步，然后向后走一步，这样做会增加整体在保持净位移不变的情况下，覆盖到任意大的距离，因此有两步向前一步的说法。

用微分重新处理上述内容，并让 {\displaystyle {\overline {AB}}}{\displaystyle {\overline {AB}}} 沿着 {\displaystyle x}x 轴，净距离微分是 {\displaystyle \mathrm {d} f=\mathrm {d} x}{\displaystyle \mathrm {d} f=\mathrm {d} x}，与反导数 {\displaystyle x}x 的精确微分。另一方面，总距离微分是 {\displaystyle |\mathrm {d} x|}{\displaystyle |\mathrm {d} x|}，它没有反导数。采取的路径是 {\displaystyle \gamma :[0,1]\to {\overline {AB}}}{\displaystyle \gamma :[0,1]\to {\overline {AB}}}时间 {\displaystyle t\in (0,1)}{\displaystyle t\in (0,1)} 使得 {\displaystyle \gamma }\gamma 在 {\displaystyle t}t 之前严格增加，之后严格减少。那么 {\displaystyle \mathrm {d} x} \mathrm{d}x 在 {\displaystyle t}t 之前为正，之后为负，得到积分，

{\displaystyle \Delta f=\int _{\gamma }\mathrm {d} x=0}{\displaystyle \Delta f=\int {\gamma }\mathrm {d} x=0}
{\displaystyle \Delta g|{\gamma }=\int _{\gamma }|\mathrm {d} x|=\int _{A}^{B}\mathrm {d} x+\int _{B }^{A}(-\mathrm {d} x)=2\int {A}^{B}\mathrm {d} x=2AB}{\displaystyle \Delta g|{\gamma }=\int _{\gamma }|\mathrm {d} x|=\int _{A}^{B}\mathrm {d} x+\int _{B}^{A}(-\mathrm {d} x)= 2\int _{A}^{B}\mathrm {d} x=2AB}
正是我们之前从口头辩论中预期的结果。

热力学第一定律

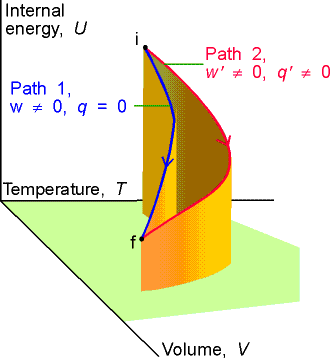
不精确的微分明显地出现在热力学第一定律中，

{\displaystyle \mathrm {d} U=\delta Q-\delta W}{\displaystyle \mathrm {d} U=\delta Q-\delta W}
其中 {\displaystyle U}U 是能量，{\displaystyle \delta Q}\delta Q 是热量的微分变化，{\displaystyle \delta W}\delta W 是功的微分变化。基于热力学系统的常数，我们能够以几种不同的方式参数化平均能量。例如，在卡诺循环（等熵）的第一阶段，一种气体被储层加热，使我们对该气体进行等温膨胀。在这个阶段，体积是恒定的，而一些不同的热量 {\displaystyle \delta Q=SdT}{\displaystyle \delta Q=SdT} 进入气体。在第二阶段，气体可以自由膨胀，输出一些不同的功 {\displaystyle \delta W=PdV}{\displaystyle \delta W=PdV}。第三阶段类似于第一阶段，除了热量通过与冷水库接触而损失，而第四循环类似于第二阶段，只是周围环境对系统做功以压缩气体。因为热和功的整体变化在循环的不同部分是不同的，所以热和功的净变化是非零的，表明差异 {\displaystyle \delta Q}\delta Q 和 {\displaystyle \delta W }\delta W 必须是不精确的微分。
内能 U 是一个状态函数，这意味着它的变化可以通过比较系统的两个不同状态（与其跃迁路径无关）来推断，因此我们可以用 U1 和 U2 来表示。由于我们可以通过提供热量 ΔQ = U2 - U1 或做功 ΔW = U2 - U1 从状态 U1 进入状态 U2，因此这种状态变化并不能唯一标识系统所做的功 W 量或传递的热量 Q，但只有内能变化ΔU。

热量和工作
火灾需要热量、燃料和氧化剂。克服燃烧的活化能势垒所需的能量以热量的形式传递到系统中，从而导致系统内部能量的变化。在一个过程中，引发火灾的能量输入可能包括功和热，例如当一个人摩擦火种（功）并经历摩擦（热）以引发火灾时。随后的燃烧是高度放热的，会释放热量。内能的整体变化并没有揭示能量传递的方式，只量化了净功和热量。系统内部能量的初始状态和最终状态之间的差异不能解释所发生的能量相互作用的程度。因此，内能是状态函数（即精确微分），而热量和功是路径函数（即不精确微分），因为积分必须考虑所采用的路径。

综合因素
有时可以通过积分因子将不精确的微分转换为精确的微分。热力学中最常见的例子是熵的定义：

{\displaystyle \mathrm {d} S={\frac {\delta Q_{\text{rev}}}{T}}}{\displaystyle \mathrm {d} S={\frac {\delta Q_{\text {rev}}}{T}}}
在这种情况下，δQ 是一个不精确的微分，因为它对系统状态的影响可以通过 δW 来补偿。然而，当除以绝对温度并且当交换发生在可逆条件下（因此是 rev 下标）时，它会产生一个精确的微分：熵 S 也是一个状态函数。
例子
考虑不精确的微分形式，

{\displaystyle \delta u=2y,\mathrm {d} x+x,\mathrm {d} y.}{\displaystyle \delta u=2y,\mathrm {d} x+x,\mathrm {d} 是的。}
考虑到点 (1,1)，这一定是不精确的。如果我们先增加 y 然后增加 x，那么这对应于首先对 y 进行积分，然后对 x 进行积分。对 y 积分首先贡献 {\textstyle \int {0}^{1}x,dy|{x=0}=0}{\textstyle \int _{0}^{1}x,dy| _{x=0}=0} 然后对 x 积分贡献 {\textstyle \int {0}^{1}2y,\mathrm {\mathrm {d} } x|{y=1}=2 }{\textstyle \int {0}^{1}2y,\mathrm {\mathrm {d} } x|{y=1}=2}。因此，沿着第一条路径，我们得到一个值 2。同样，沿着第二条路径，我们得到一个值 {\textstyle \int {0}^{1}2y,\mathrm {d} x|{y =0}+\int {0}^{1}x,\mathrm {d} y|{x=1}=1}{\textstyle \int {0}^{1}2y,\ mathrm {d} x|{y=0}+\int {0}^{1}x,\mathrm {d} y|{x=1}=1}。我们可以通过将 {\displaystyle \delta u}{\displaystyle \delta u} 乘以 x 使之成为精确微分，得到
{\displaystyle x,\delta u=2xy,\mathrm {d} x+x^{2},\mathrm {d} y=\mathrm {\mathrm {d} } (x^{2}y )}{\displaystyle x,\delta u=2xy,\mathrm {d} x+x^{2},\mathrm {d} y=\mathrm {\mathrm {d} } (x^{2 }y)}
.所以 {\displaystyle x,\delta u}{\displaystyle x,\delta u} 是一个精确的微分。

---

• 参考资料：

Inexact differential

不完全微分

Exact differential

Gradient theorem