当前位置：网站首页>Chapter 10 Clustering

Chapter 10 Clustering

2022-08-02 03:28:00 【Sang Zhiwei 0208】

1 Methods of similarity measurement and correlation

1.1 方法

闵可夫斯基Minkowski/欧式距离 $dist(X,Y)=(\sum _{i=1}^{n} |x_{i}-y_{i}|^{p})^{\frac{1}{p}}$

杰卡德相似系数（Jaccard） $J(A,B)=\frac{|A\bigcap B|}{|A\bigcup B|}$

余弦相似度 $cos(\theta )=\frac{a^{T}b}{|a|\cdot |b|}$

Pearson相似系数 $\rho _{XY}=\frac{cov(X,Y)}{\sigma _{X}\sigma _{Y}}=\frac{E[(X-\mu _{X})(Y-\mu _{Y})]}{\sigma _{X}\sigma _{Y}}=\frac{\sum _{i=1}^{n}(X_{i}-\mu _{X})(Y_{i}-\mu _{Y})}{\sqrt{\sum _{i=1}^{n}(X_{i}-\mu _{X})^{2}}\sqrt{\sum _{i=1}^{n}(Y_{i}-\mu _{Y})^{2}}}$

相对熵（K-L距离） $D(p||q)=\sum _{x}p(x)log\frac{p(x)}{q(x)}=E_{p(x)}\frac{p(x)}{q(x)}$

Hellinger距离 $D_{\alpha }(p||q)=\frac{2}{1-\alpha ^{2}}(1-\int p(x)^{\frac{1+\alpha }{2}}q(x)^{\frac{1-\alpha }{2}}dx)$

ps:假设 $(x_{1}-x_{2})$ 最大,则 $\underset{p\rightarrow \infty }{lim}[(x_{1}-x_{2})^{p}+(y_{1}-y_{2})^{p}+(z_{1}-z_{2})^{p}]^{\frac{1}{p}}=\underset{p\rightarrow \infty }{lim}[(x_{1}-x_{2})(1+(\frac{(y_{1}-y_{2})}{(x_{1}-x_{2})})^{p}+(\frac{(z_{1}-z_{2})}{(x_{1}-x_{2})})^{p}]^{\frac{1}{p}}=(x_{1}-x_{2})$

1.2 相互联系

Cosine similarity with PearsonThe relationship between the similarity coefficients：

n维向量x和y的夹角记做 $\theta$ ,根据余弦定理,其余弦值为： $cos(\theta )=\frac{x^{T}y}{|x|\cdot |y|}=\frac{\sum_{i=1}^{n}x_{i}y_{i}}{\sqrt{\sum_{i=1}^{n}x_{i}^{2}}\sqrt{\sum_{i=1}^{n}y_{i}^{2}}}$

The correlation coefficient of these two vectors is ：

$\rho _{XY}=\frac{cov(X,Y)}{\sigma _{X}\sigma _{Y}}=\frac{E[(X-\mu _{X})(Y-\mu _{X})]}{\sigma _{X}\sigma _{Y}}=\frac{\sum_{i=1}^{n}(x_{i}-\mu_{X} )(y_{i}-\mu _{Y})}{{\sqrt{\sum _{i=1}^{n}(X_{i}-\mu _{X})^{2}}\sqrt{\sum _{i=1}^{n}(Y_{i}-\mu _{Y})^{2}}} }$

相关系数就是将x,y坐标向量各自平移到原点后的夹角余弦.

2 K-meansClustering ideas and conditions of use

2.1 定义

聚类就是对大量未知标注的数据集,按数据的内在相似性将数据集划分为多个类别,使类别内的数据相似度较大而类别间的数据相似度较小.是一种无监督学习.

2.2 思路

基本思想：对于给定的类别数目k,首先给出初始划分,通过迭代改变样本和簇的隶属关系,使得每一次改进之后的划分方案都较前一次好.

2.3 使用条件

给定一个有N个对象的数据集,构造数据的k个簇, $k\leq n$ .满足下列条件：
（1）每一个簇至少包含一个对象

（2）每一个对象属于且仅属于一个簇

（3）将满足上述条件的k个簇称作一个合理划分

2.4 算法

k-Means将簇中所有点的均值作为新质心,But if the cluster contains outliers,will lead to a serious deviation from the mean.因此,In this case it is safer to use the median of all points in the cluster as the new centroid,This clustering method is called k-Mediods聚类.
The choice of the initial value is artificial.

2.5 k-means的公式化解释

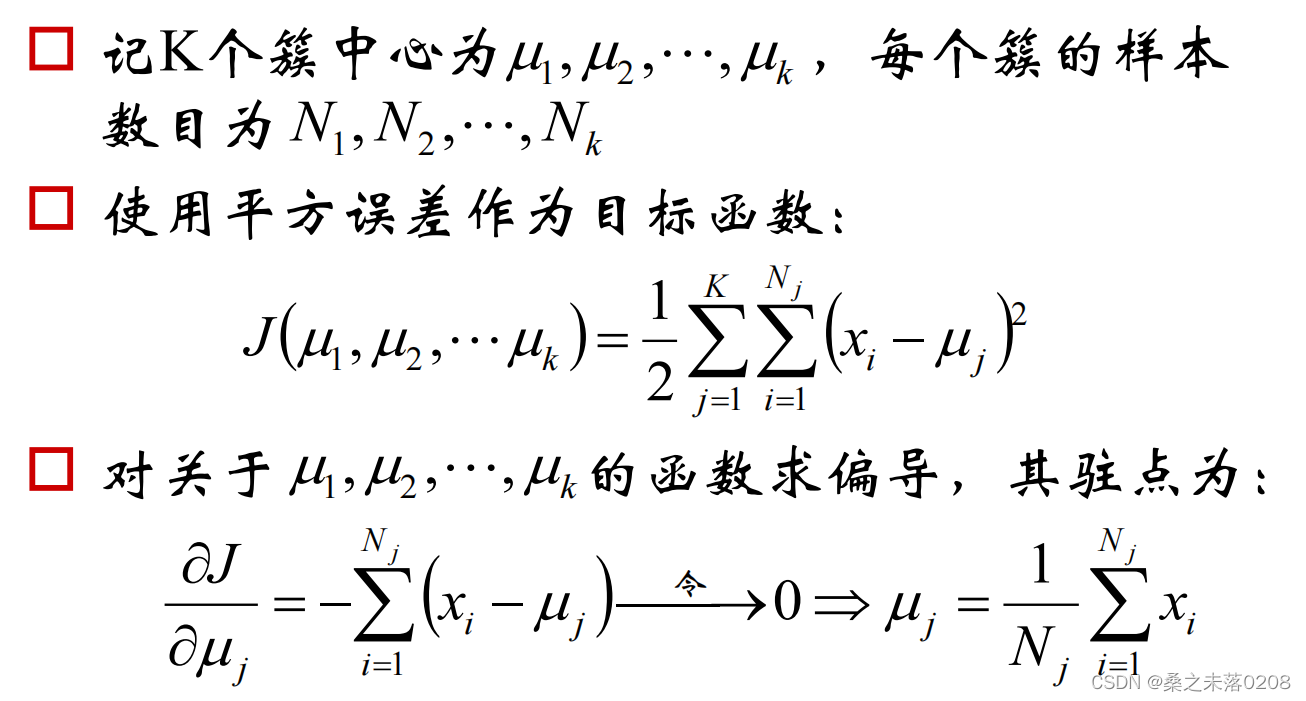
2.6 聚类的衡量指标

均一性：一个簇只包含一个类别的样本,则满足均一性.
完整性：同类别样本被归类到相同簇中,则满足完整性.
PS:Uniformity and completeness are the opposite,If the uniformity is good, the integrity is not very good;If the integrity is good, the uniformity is not very good.

2.7 k-meansSummary of clustering methods

优点：

是解决聚类问题的一种经典算法,简单、快速
对处理大数据集,该算法保持可伸缩性和高效率
当簇近似为高斯分布时,它的效果较好

缺点：

在簇的平均值可被定义的情况下才能使用,可能不适用于某些应用
必须事先给出k(要生成的簇的数目),而且对初值敏感,对于不同的初始值,可能会导致不同结果.
不适合于发现非凸形状的簇或者大小差别很大的簇
对躁声和孤立点数据敏感

可作为其他聚类方法的基础算法,如谱聚类

2.8 聚类模型

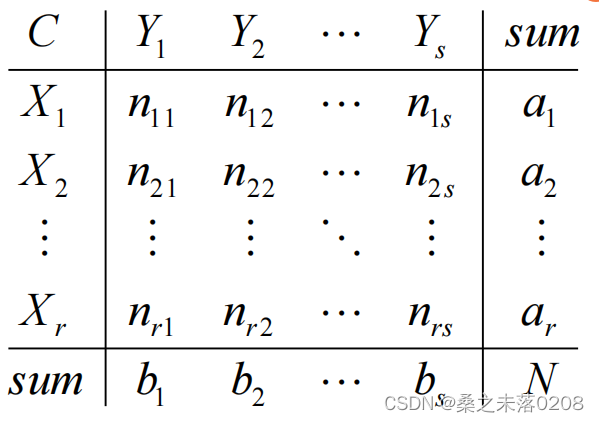
(1) ARI：

数据集S共有N个元素,两个聚类结果分别是： $X=\left \{ X_{1},X_{2},...,X_{r} \right \},Y=\left \{ Y_{1},Y_{2},...,Y_{s} \right \}$

X和Y的元素个数为： $a=\left \{ a_{1},a_{2},...,a_{r} \right \},b=\left \{ b_{1},b_{2},...,b_{s} \right \}$

记： $n_{ij}=|X_{i}\bigcap Y_{i}|$

则： $ARI=\frac{Index-EIndex}{MaxIndex-EIndex}=\frac{\sum_{i,j}C_{n_{ij}}^{2}-\frac{[\sum_{i}C_{b_{j}}^{2}\cdot \sum_{j}C_{b_{j}}^{2}]}{C_{n}^{2}}}{\frac{1}{2}\frac{[\sum_{i}C_{a_{i}}^{2}+\sum_{j}C_{b_{j}}^{2}]-[\sum_{i}C_{b_{j}}^{2}\cdot \sum_{j}C_{b_{j}}^{2}]}{C_{n}^{2}}}$

(2) AMI

The mutual information is obtained according to the information entropy/regularization information：

$MI(X,Y)=\sum_{i=1}^{r}\sum_{j=1}^{s}P(i,j)log\frac{p(i,j)}{P(i)P(j)}$

$NMI(X,Y)=\frac{MI(X,Y)}{\sqrt{H(X)H(Y)}}$

X服从超几何分布,The expectation of the mutual information sought is ：

$E(MI) = \sum_{x} ^{} P(X=x) MI(X,Y) = \sum_{x=max(1,a_{i}+b_{i}-N)}^{min(a_{i},b_{i})}[MI\cdot \frac{a_{i}!b_{j}!(N-a_{i})!(N-b_{j})!}{N!x!(a_{i}-x)!(b_{j}-x)!(N-a_{i}-b_{j}+x)!}]$

从而有： $AMI(X,Y)=\frac{MI(X,Y)-E[MI(X,Y)]}{max\left \{ H(X),H(Y) \right \}-E[MI(X,Y)]}$

2.9 轮廓系数

3 Ideas and methods of hierarchical clustering

3.1 思路

层次聚类方法对给定的数据集进行层次的分解,直到某种条件满足为止.

分两种：

（1）凝聚的层次聚类：AGNES算法——一种自底向上的策略.首先将每个对象作为一个簇,然后合并这些原子簇为越来越大的簇,直到某个终结条件被满足.

（2）分裂的层次聚类：DIANA算法——采用自顶向下的策略.首先将所有对象置于一个簇中,然后逐渐细分为越来越小的簇,直到达到了某个终结条件.

3.2 算法

4 密度聚类

4.1 介绍

指导思想——只要样本点的密度大于某阈值,则将该样本添加到最近的簇中.

优点——能克服基于距离的算法只能发现“类圆形”（凸）的聚类的缺点,可发现任意形状的聚类,且对噪声数据不敏感.But the computational complexity of computing the density unit is greater,需要建立空间索引来降低计算量.

4.2 密度聚类模型

DBSCAN算法

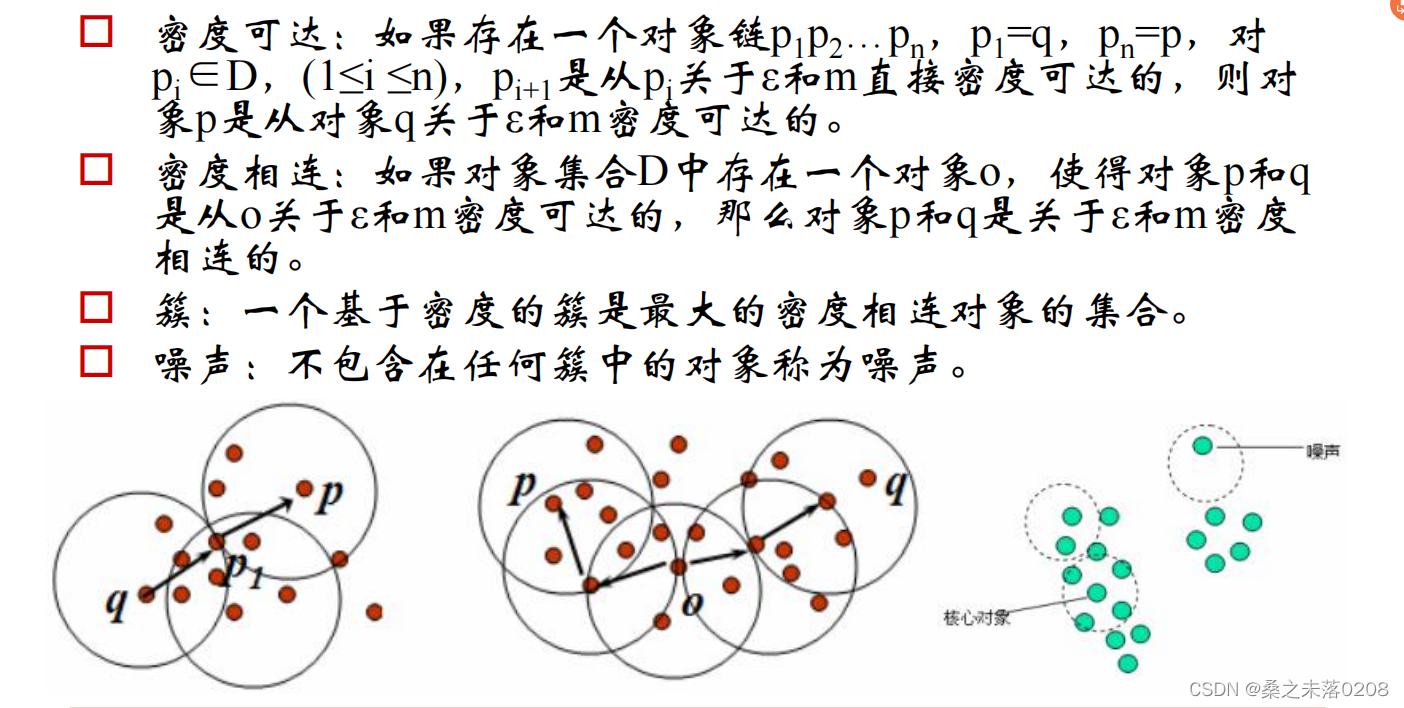
密度最大值聚类

5 Review eigenvalues

（1）实对称阵的特征值是实数

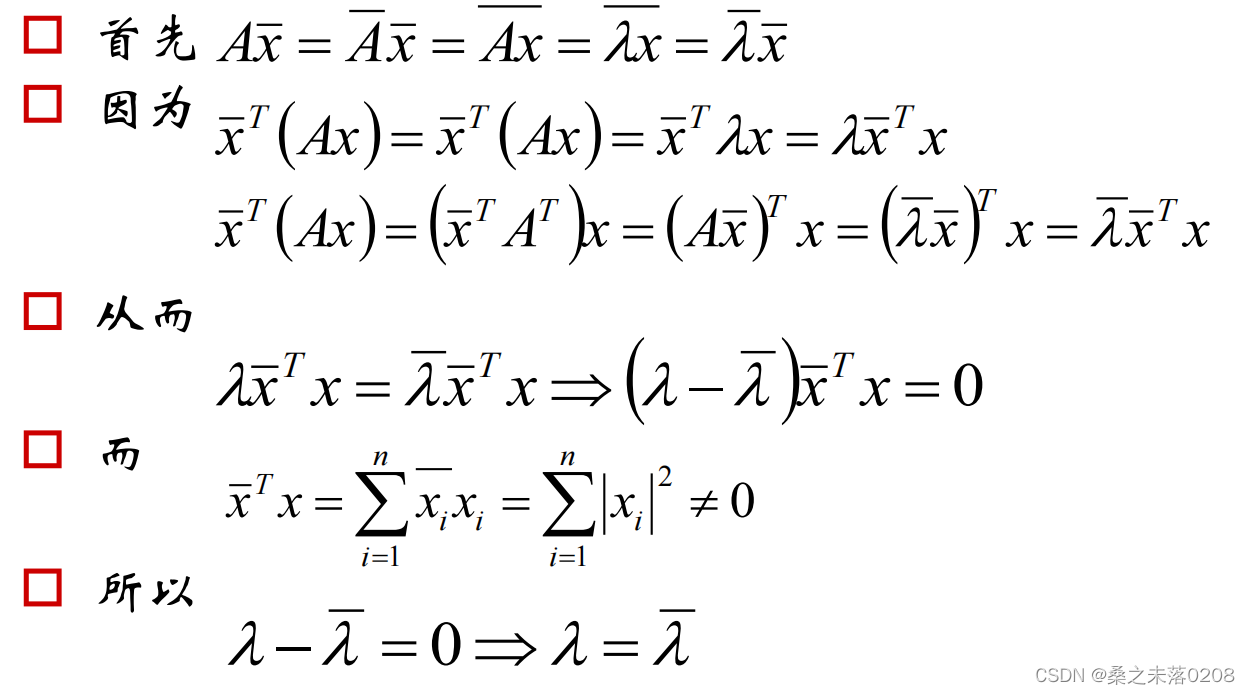
（2）实对称阵不同特征值的特征向量正交

6 谱和谱聚类

方阵作为线性算子,它的所有特征值的全体统称方阵的谱.

方阵的谱半径为最大的特征值
矩阵A的谱半径：（ $A^{T}A$ ）的最大特征值

谱聚类是一种基于图论的聚类方法,通过对样本数据的拉普拉斯矩阵的特征向量进行聚类,从而达到对样本数据聚类的目的.

The matrix formed by the samples $W=(w_{ij})$ , 取第iThe weights of the rows are added asdi,即第idegree of sample,组成矩阵D.求L前kThe eigenvectors corresponding to the small eigenvalues are formedu矩阵,对它做k均值,The final result of general clustering is obtained.