当前位置:网站首页>积分简明笔记-第一类曲线积分的类型
积分简明笔记-第一类曲线积分的类型
2022-07-30 07:55:00 【繁星依月】
第一类曲线积分的类型
一、第一类曲线积分的分类
01 平面第一类曲线积分
若 Γ A B ⊂ R 2 \Gamma_{AB}\subset\mathrm{R}^2 ΓAB⊂R2, P ( x , y ) ∈ Γ A B P(x,y)\in\Gamma_{AB} P(x,y)∈ΓAB,
∫ Γ A B f ( P ) d s = ∫ Γ A B f ( x , y ) d s \int_{\Gamma_{AB}}f(P)ds=\int_{\Gamma_{AB}}f(x,y)ds ∫ΓABf(P)ds=∫ΓABf(x,y)ds 称为平面第一类曲线积分。
02 空间第一类曲线积分
若 Γ A B ⊂ R 3 \Gamma_{AB}\subset\mathrm{R}^3 ΓAB⊂R3, P ( x , y , z ) ∈ Γ A B P(x,y,z)\in\Gamma_{AB} P(x,y,z)∈ΓAB,
∫ Γ A B f ( P ) d s = ∫ Γ A B f ( x , y , z ) d s \int_{\Gamma_{AB}}f(P)ds=\int_{\Gamma_{AB}}f(x,y,z)ds ∫ΓABf(P)ds=∫ΓABf(x,y,z)ds 称为空间第一类曲线积分。
第一类曲线积分可以求平面和空间的曲线弧长。
二、第一类曲线积分的计算
01 平面第一类曲线积分
(1) 一元函数型
形式: Γ A B : y = φ ( x ) , x ∈ [ a , b ] \Gamma_{AB}:y=\varphi(x),x\in[a,b] ΓAB:y=φ(x),x∈[a,b] (x=x) 特殊的参数方程
φ ’ ( x ) \varphi’(x) φ’(x) 连续(以后默认)
∫ Γ A B f ( x , y ) d s = ∫ a b f ( x , φ ( x ) ) 1 + φ ′ 2 ( x ) d x \int_{\Gamma_{AB}}f(x,y)ds=\int_{a}^{b}f(x,\varphi(x))\sqrt{1+\varphi'^2(x)}\ dx ∫ΓABf(x,y)ds=∫abf(x,φ(x))1+φ′2(x) dx
(2) 一元反函数型
形式: Γ A B : x = ψ ( y ) , y ∈ [ c , d ] , ψ ’ ( x ) \Gamma_{AB}:x=\psi(y)\ , \ y\in[c,d]\ , \ \psi’(x) ΓAB:x=ψ(y) , y∈[c,d] , ψ’(x) 连续 ( y = y y=y y=y ) 特殊的参数方程
∫ Γ A B f ( x , y ) d s = ∫ c d f ( ψ ( y ) , y ) 1 + ψ ′ 2 ( y ) d y \int_{\Gamma_{AB}}f(x,y)ds=\int_{c}^{d}f(\psi(y),y)\sqrt{1+\psi'^2(y)}\ dy ∫ΓABf(x,y)ds=∫cdf(ψ(y),y)1+ψ′2(y) dy
(3) 极坐标型
形式: Γ A B : r = r ( θ ) , θ ∈ [ α , β ] , r ′ ( θ ) \Gamma_{AB}:r=r(\theta)\ , \ \theta\in[\alpha,\beta]\ , \ r'(\theta) ΓAB:r=r(θ) , θ∈[α,β] , r′(θ) 连续
⇒ { x = r ( θ ) cos θ y = r ( θ ) sin θ θ ∈ [ α , β ] \Rightarrow\ \begin{cases}\ x=r(\theta)\cos\theta \\ \ y=r(\theta)\sin\theta\end{cases}\quad\theta\in[\alpha,\beta] ⇒ { x=r(θ)cosθ y=r(θ)sinθθ∈[α,β] , x ′ 2 ( θ ) + y ′ 2 ( θ ) = r 2 ( θ ) + r ′ 2 ( θ ) x'^2(\theta)+y'^2(\theta)=r^2(\theta)+r'^2(\theta) x′2(θ)+y′2(θ)=r2(θ)+r′2(θ),强行构造参数方程
∫ Γ A B f ( x , y ) d s = ∫ α β f ( r ( θ ) cos θ , r ( θ ) sin θ ) r 2 ( θ ) + r ′ 2 ( θ ) d θ \int_{\Gamma_{AB}}f(x,y)ds=\int_{\alpha}^{\beta}f(r(\theta)\cos\theta,r(\theta)\sin\theta)\sqrt{r^2(\theta)+r'^2(\theta)}\ d\theta ∫ΓABf(x,y)ds=∫αβf(r(θ)cosθ,r(θ)sinθ)r2(θ)+r′2(θ) dθ
(4) 反极坐标型
形式: Γ A B : θ = θ ( r ) , r ∈ [ a , b ] , θ ′ ( r ) \Gamma_{AB}:\theta=\theta(r)\ , \ r\in[a,b]\ , \ \theta'(r) ΓAB:θ=θ(r) , r∈[a,b] , θ′(r) 连续
⇒ { x = r cos θ ( r ) y = r sin θ ( r ) r ∈ [ a , b ] \Rightarrow\ \begin{cases}\ x=r\cos\theta(r) \\ \ y=r\sin\theta(r)\end{cases}\quad r\in[a,b] ⇒ { x=rcosθ(r) y=rsinθ(r)r∈[a,b]
不作统一形式的公式,具体题目具体分析。
好的思路:转化为 r = r ( θ ) r=r(\theta) r=r(θ) 或者关于x,y的方程。
02 空间第一类曲线积分
若 Γ A B : { x = x ( t ) y = y ( t ) z = z ( t ) t ∈ [ α , β ] \Gamma_{AB}:\ \begin{cases}\ x=x(t) \\ \ y=y(t) \\ \ z=z(t)\end{cases}\quad t\in[\alpha,\beta] ΓAB: ⎩⎨⎧ x=x(t) y=y(t) z=z(t)t∈[α,β],则有
∫ Γ A B f ( x , y , z ) d s = ∫ α β f ( x ( t ) , y ( t ) , z ( t ) ) x ′ 2 ( t ) + y ′ 2 ( t ) + z ′ 2 ( t ) d t \int_{\Gamma_{AB}}f(x,y,z)ds=\int_{\alpha}^{\beta}f(x(t),y(t),z(t))\sqrt{x'^2(t)+y'^2(t)+z'^2(t)}\ dt ∫ΓABf(x,y,z)ds=∫αβf(x(t),y(t),z(t))x′2(t)+y′2(t)+z′2(t) dt
重积分被积函数一般不能化简,因为它满足的是不等式,而曲线曲面积分经常可以化简,因为它满足的是等式。
边栏推荐
猜你喜欢

typescript7-typescript common types
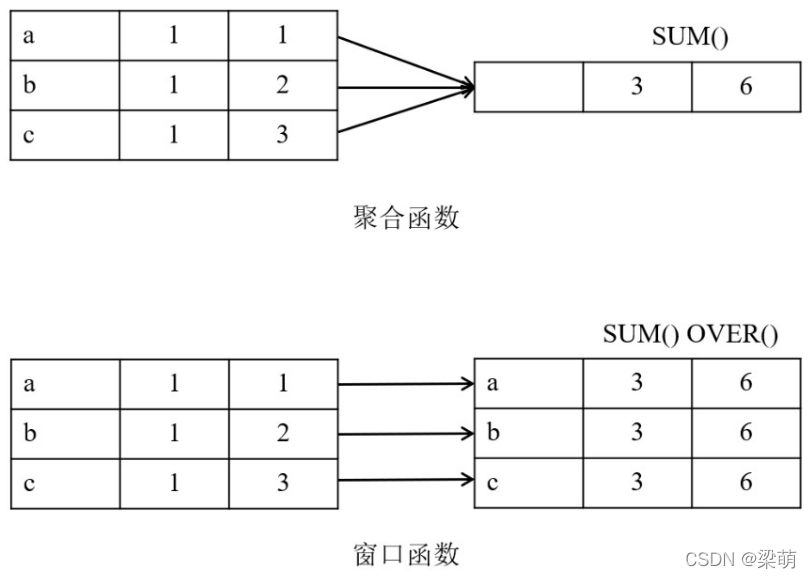
SQL窗口函数

Leetcode - 990: equations of satisfiability

阿里云国际版云服务器防火墙设置

typescript4 - installs a toolkit for compiling ts

Why does typescript2-typescript add type support to js

剖析SGI STL空间配置器(allocate内存分配函数)

hcip第八天
![[Mini Program Column] Summarize the development specifications of uniapp to develop small programs](/img/7b/110d324eba00652e4987bc623a5bc6.png)
[Mini Program Column] Summarize the development specifications of uniapp to develop small programs

leetcode经典问题——11.盛水最多的容器
随机推荐
SQL row-column conversion
Kubernetes 在科技革命中的演变
【无标题】
[Mini Program Column] Summarize the development specifications of uniapp to develop small programs
基于JSP实现校园二手交易平台
SQL的substring_index()用法——MySQL字符串截取
基于SSM实现个性化健康饮食推荐系统
hicp第六天
One article to understand twenty kinds of switching power supply topologies
风靡全球25年的重磅IP,新作沦为脚本乐园
input标签的tabindex属性 & a标签的tabindex属性
typescript6-简化运行ts的步骤
It is said that FPGA is high-end, what can it do?
【三子棋】——玩家VS电脑(C语言实现)
hcip实验
函数(1)
typescript6 - simplify the steps to run ts
EMC过不了?都是PCB工程师的锅?
基于SSM开发实现校园疫情防控管理系统
剑指offer 48:最长不重复子串