当前位置:网站首页>Storage of data in memory
Storage of data in memory
2022-07-07 09:06:00 【A big cat 1201】
author : A big cat 1201
special column :《C Language learning 》
Maxim : You just try to , Leave the rest to time !
List of articles
describe
We are using C When it comes to language , Some data will be used , There are many types of data , Every data is stored in memory , It's like every one of us has his own house , Data also has a place to live in memory , And there are their own storage methods , Let's first introduce the storage of some data .
data type
There are types of data , They can be divided into several categories .
1️⃣ The integer family
- char type :
We have always had the impression char Type is character type , This type of variable contains characters , for example ’a’,’ ‘,‘b’,‘i’,‘g’,’ ',‘c’,‘a’,‘t’. Including letters, spaces, etc , One character takes up one byte .
But the appearance of these characters in memory is not the original character , It is a ASCII Store by code value ,ASCII Code value from 0 To 127 Represent different characters , therefore char Type is also integer .
It is divided into :
char
unsigned char
signed char
char The type is quite special , stay C There is no stipulation in the language sign char Is it signed or not , Different compilers have different standards , Used by benmew VS2019 In the compiler char It's a symbolic type .
- short type :
unsigned short
signed short
short Types only have unsigned and signed types ,short Belonging to the signed type , Size is 2 Bytes .
- int type :
unsigned int
signed int
int Types only have unsigned and signed types ,int Belonging to the signed type , Size is 4 Bytes .
- long type :
unsigned long
signed long
long Types only have unsigned and signed types ,long Belonging to the signed type , Size is 4 perhaps 8 Bytes .
C Language standards ,long>=int Just go , So it's in 32 Bit platform is 4 Bytes , stay 64 Bit platform is 8 Byte size .
- long long type :
This type is C99 Standard only , Size is 8 Bytes , It's usually not used .
2️⃣ Floating point family
- float type :
It is called single precision floating-point data , Its accuracy is relatively low , The default output is six decimal places .
- double type :
It is called double precision floating-point data , Its precision is relatively high , The default output is also six decimal places . Later, Ben meow will explain why it has high accuracy .
As long as your data is decimal , You have to use one of these two .
3️⃣ Construction type
- An array type
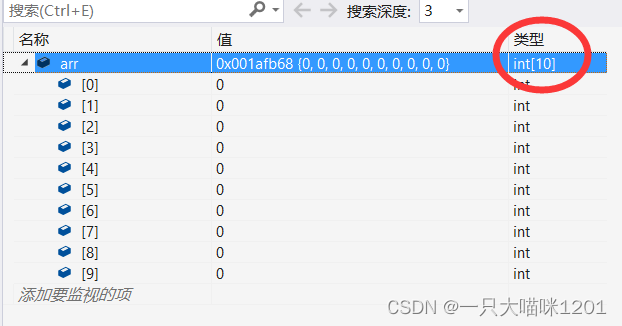
This one has 10 Array of elements , Its type is int[10], That is, remove the array name from the array , The rest is the type of the array , So array types are diverse , Different element types , Number of different elements , Array types vary , Its type is determined by the user , So it is a construction type .- Type of structure stuct
- Consortium type union
- Enumeration type enum
These are all construction types , They are of various types , Users can construct whatever type they want . The latter three types will be explained by special topics in the future .
4️⃣ Pointer types
- int *pi;
- char *pc;
- float* pf;
- void* pv;
The pointer will also be explained in detail later .
5️⃣ Empty type
void Indicates empty type ( No type )
Usually applied to the return type of a function 、 The parameters of the function 、 Pointer types .
Here, I will only introduce the storage of integer data and floating-point data in memory .
Storage of integer data
The first thing to know is , There are many ways to express a number , Yes
10 Hexadecimal said ( The most commonly used )
8 Hexadecimal said
16 Hexadecimal said
2 Hexadecimal said
…
A computer is made up of many circuit elements , The circuit state is generally represented by two stable and convertible States, high level or low level , So will 0 It is regarded as low level ,1 As high level .
therefore , The data stored in memory is 0 perhaps 1, That is to say 2 Hexadecimal way to store data .
and 2 Hexadecimal has three forms :
Original code
Inverse code
Complement code
Code up :
#include <stdio.h>
int main()
{
int a = 10;
int b = -10;
return 0;
}
These are the two integers we created , Namely 10 and -10.
Next, let's talk about their representation rules :
the reason being that int type , Size is 4 Bytes , So convert to 2 Base or by 32 individual 0 and 1 form .
Positive numbers 10
Original code :00000000000000000000000000001010
Inverse code :00000000000000000000000000001010
Complement code :00000000000000000000000000001010
The above is the original code of positive numbers , Inverse code , Complement code , It's all the same , highest 0 The representative symbol is , rest 31 Arrays are numeric bits .
negative -10
Original code :10000000000000000000000000001010
Inverse code :111111111111111111111111111111110101
Complement code :111111111111111111111111111111110110
The above is the original code of negative numbers , Inverse code , Complement code , They are different , Need to compute . Normal indicates the original code , The inverse code is the highest bit, that is, the symbol remains unchanged , Other bits are reversed , Complement is the inverse code plus 1.
So these 0 and 1 How is it stored in memory ?
For the sake of convenience , We write these two numbers as 16 The form of base , It's just that the form has changed , But their essence is still 2 Base number .
Positive numbers 10
Original code :00 00 00 0a
Inverse code :00 00 00 0a
Complement code :00 00 00 0a
take 10 Write it in hexadecimal according to the binary above .
negative -10
Original code :00 00 00 0a
Inverse code :ff ff ff f5
Complement code :ff ff ff f6
take -10 Write it in hexadecimal according to the binary above .
Next, let's debug , Observe what these two numbers look like in memory .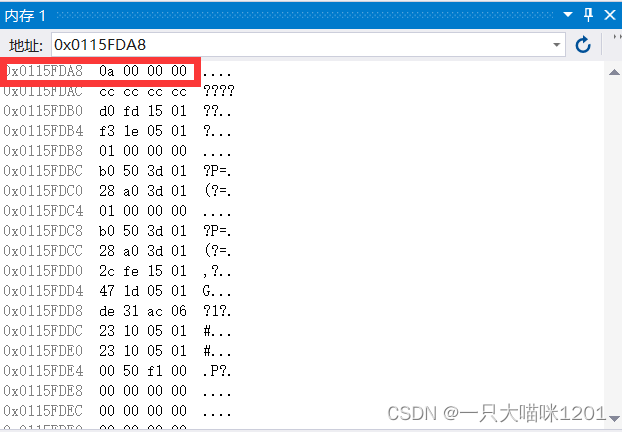
This is a a That's a positive number 10 What it looks like in memory , It is 0a 00 00 00, Compared with the above analysis 10 The original code of , Inverse code , The complement is the same , Size is 4 Bytes ( Ignore the problem that it is stored upside down ).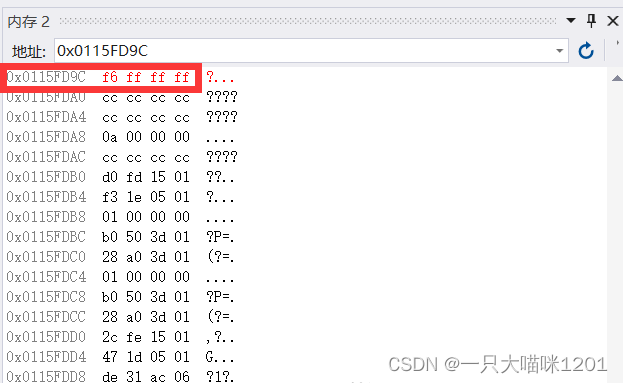
This is a b That's negative -10 What it looks like in memory , It is f6 ff ff ff, Compared with the above analysis -10 The complement of is the same , Size is 4 Bytes ( Ignore the problem that it is stored upside down ).
By observing positive numbers 10 And negative numbers -10 What it looks like in memory , We found that the appearance in memory is the complement of these two numbers .
So come to the conclusion , Integer data is stored in memory in the form of complement . The entire integer family mentioned above stores data in this way .
Is there such a question , Why is not the original code stored in the memory ? How easy to use the original code , Take it out and you can use it , If it is a negative number, there is no need to convert , This is really convenient for users , But the computer hardware will be more complex , There are several reasons for storing complement :
- Complement can unify the symbolic field and numerical field of data . That is, in the process of calculation, the symbol bit is also directly involved in the operation , There is no need to distinguish between sign bits and numeric bits .
- CPU Only adders . in other words ,CPU You can only add , You cannot use subtraction , When two numbers want to be reduced ,CPU Regard it as the complement of a positive number and the complement of a negative number to add , The essence is to subtract two numbers .
- The conversion logic of source code and complement code is the same , No need for additional hardware circuits . It has been said above that the original code is converted into complement , The logic of converting complement into original code is the same , Because the complement of the complement is the original code .
In debugging , Have you found a strange phenomenon ?
This is a positive number 10 Stored in memory ,10 The complement of is 00 00 00 0a, The framed part in the picture is 4 Byte size , That is to say 1 individual int type , Its address is int The address of the first byte in the type , therefore 10 This int The address and contents of the space occupied by the type are
0x0115FDA8 0a
0x0115FDA9 00
0x0115FDAA 00
0x0115FDAB 00
ah ?
We found that the data is placed upside down , Not according to 00 00 00 0a Put the order here 4 One of the addresses , This involves the next content , Large and small end storage .
Big ( Small ) End byte order storage mode
Let's first introduce its concept
Large endian storage : The low bit of data is stored in the high address of memory , And the high end of the data , Stored in a low address in memory .
Small end byte order storage : The low bit of data is stored in the low address of memory , And the high end of the data ,, Stored in a high address in memory .
And positive numbers 10 Expressed in hexadecimal 00 00 00 0a in , The lowest byte is 0a, The leftmost 00 Is the highest byte .
It's like this in the form of a graph , Obviously , This is a small end byte order storage mode . So we can see that the data in memory looks upside down .
Big ( Small ) End byte order storage mode , Byte order is the key , It is stored in bytes , So it's not just integers , Floating point types are also stored in this way , Also with 1 Bytes as a unit to store .
Since it's just a sequential way , You can also store them in different order , For example, according to 
Save the highest position first , Save the lowest bit , Save again high , Store in the order of the next lowest order , As long as you take it out in this storage order when you use it . But normal people will not put it like this , Only choose one of the big end or small end to store .
Whether to use big endian byte order storage or small endian byte order storage depends on the compiler , Used by benmew VS2019 The compiler uses a small end storage method , phase keil5 The big end byte order storage mode is adopted .
Some examples of integer storage ( Skipping )
Example 1:
#include <stdio.h>
int main()
{
char a = -128;
printf("%u\n", a);
return 0;
}
What is the output result of the above example ? Is your first reaction -128 Well ? If it is , congratulations , Drop the pit
Let's analyze .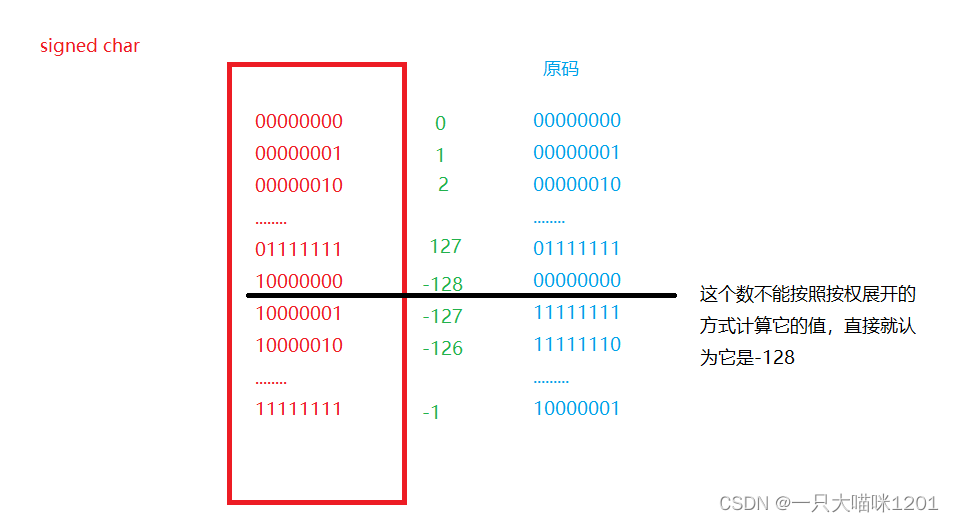
This is a char type , That is to say signed char The range of values that can be stored in the type , Size is -128 To 127.
First we give a The assignment is a int type -128, its
Original code :10000000000000000000000010000000
Inverse code :111111111111111111111111101111111
Complement code :111111111111111111111111110000000
Because I want to put this 4 Byte size int The complement of type data is placed in 1 Byte size char Type in the , So truncation happens , Truncate from position , therefore a In memory, it looks like
Complement code :10000000
The data type to be printed is %u, yes unsigned int Data of type , So in memory a Integer promotion will occur , Promotion is based on the sign bit , In memory at this time a The sign bit of is 1, So the result of promotion is
Complement code :11111111111111111111111110000000
Because it is unsigned int Type of , Unsigned integer , At this time, the highest bit does not represent the sign bit , It's a numeric bit , So at this time, so in the complement 0 and 1 Are all numeric bits , So the result is converted to decimal 4,294,967,168.

You can see , The running result is consistent with our analysis .
Example 2:
#include <stdio.h>
int main()
{
char a = 128;
printf("%u\n", a);
return 0;
}
What is the result of this ? yes 128 Do you ? Let's analyze .
int type 128 Of
Original code :00000000000000000000000010000000
Inverse code :00000000000000000000000010000000
Complement code :00000000000000000000000010000000
Because it's a positive number , So the original , Inverse code , The complement is the same .
Put it in char Type of a After truncation in variable
Complement code :10000000
Print is unsgined int type , After integer lifting
Complement code :11111111111111111111111110000000
The result of treating all as numerical bits is 4,294,967,168.
You can see , After truncation , Data and examples in memory 1 It's the same , So the final result is the same .
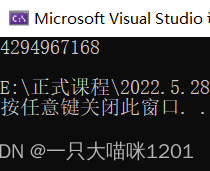
This is its result , Sure enough, with examples 1 The same as .
Example 3:
#include <stdio.h>
int main()
{
int i = -20;
unsigned int j = 10;
printf("%d\n", i + j);
return 0;
}
What is the output of this code ? Dare not say yes -10 了 , Pit Scared ? ha-ha , The result is -10.
Let's analyze
int type i = -20 Of
Original code :10000000000000000000000000010100
Inverse code :11111111111111111111111111101011
Complement code :11111111111111111111111111101100
unsigned int type j = 10 Of
Original code :00000000000000000000000000001010
Inverse code :00000000000000000000000000001010
Complement code :00000000000000000000000000001010
int The type and unsigned int Arithmetic conversion occurs when types are added ,int Type to bit unsigned int type , After the transformation ,int Type is i The highest bit in is no longer a sign bit , It's a numeric bit . After adding
Complement code :11111111111111111111111111110110
And the print is %d Some, that is int type , So you need to calculate the original complement in memory
Complement code :11111111111111111111111111110110
Inverse code :10000000000000000000000000001001
Original code :10000000000000000000000000001010
After converting to decimal, the result is -10.

We can see , The result is -10.
Example 4:
#include <stdio.h>
int main()
{
unsigned int i;
for (i = 9; i >= 0; i--)
{
printf("%u\n", i);
}
return 0;
}
What is the result of this code ? It's from 9 To 0 Do you ? Let's analyze
First of all, I will definitely print from 9 To 0, When i yes 0 When , its
Complement code :00000000000000000000000000000000
️
Except after the cycle 0 It will be reduced again 1, reduce 1 After
Complement code :11111111111111111111111111111111
️
because i The type is unsgined int type , There is no sign bit , The highest bit is also regarded as a numeric bit , So this minus 1 The result is not a negative number , It is 4,294,967,295 Such a large number . Reduce this number gradually and print it again and again , When it comes to 0 when , Re reduction 1 It becomes such a big number again , So it's an endless cycle .
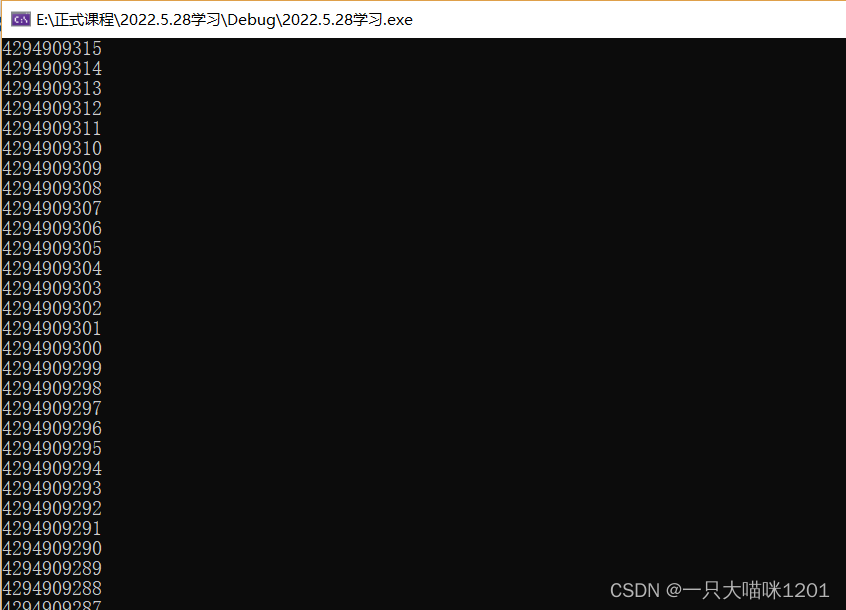
You can see , The number keeps decreasing .
Example 5:
int main()
{
char a[1000];
int i;
for (i = 0; i < 1000; i++)
{
a[i] = -1 - i;
}
printf("%d", strlen(a));
return 0;
}
What is the result of this code ?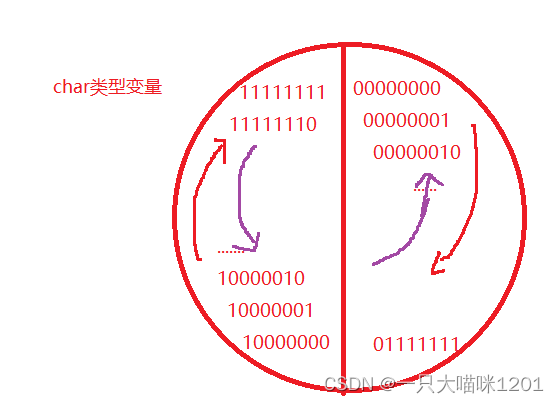
This disc imitates a char Variable of type , When you press the red arrow to rotate clockwise , It's from 0 Start adding 1, When added to 01111111 That is to say 127 When , add 1 It becomes 10000000 That is to say -128 了 , Gradually add 1 It becomes -1, add 1 And then it becomes 0. because char The type is numeric and the range is -128 To 127, No matter what, it won't go out of this range .
When the purple arrow rotates counterclockwise , That is to say, minus 1 when
from 11111111 That is to say -1 Begin to reduce 1, When it comes to 10000000 That is to say -128 When , Re reduction 1 It becomes 0111111 That is to say 127 了 , Continue to reduce 1 Will be reduced to 00000000 That is to say 0.
️
strlen() The function counts ‘\0’ Number of previous characters , and ’\0’ Of ASCII The code value is 0, So the numerical a The values in are expressed in ASCII The formal representation of code value is from -1 To -128, Again from 127 To 0, altogether 256 Characters , And because there is no statistics 0 That is to say ‘\0’, So there is 255 Characters , So the length of this string is 255.

The result is 255.
Example 6:
#include <stdio.h>
unsigned char i = 0;
int main()
{
for (i = 0; i <= 255; i++)
{
printf("hello world\n");
}
return 0;
}
What is the result of this code ?
Several examples are analyzed above , At a glance, my friends saw the answer
The answer is dead cycle printing
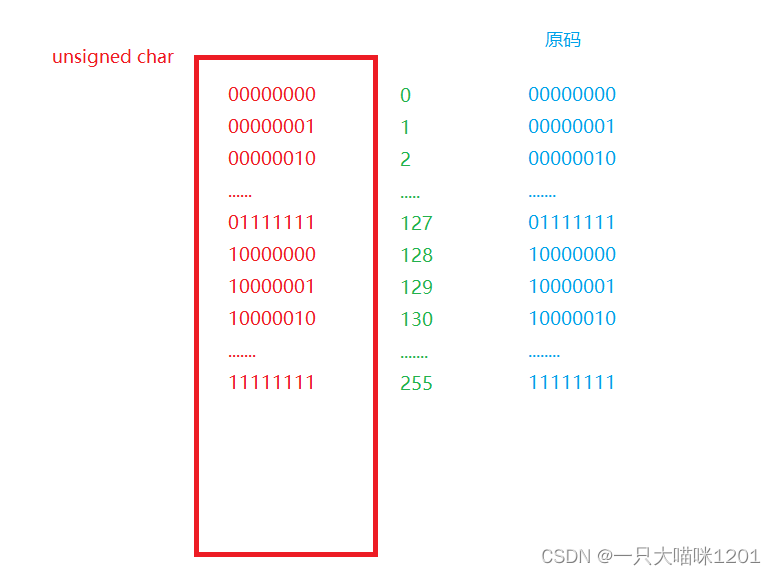
This is a unsigned char Type of data storage , The range of values is 0 To 255.
So the above code will cycle first 0-255 common 266 Time , That is, printing 266 Time , When i become 255 in the future , add 1 Will overflow , It will become 00000000 That is to say 0, Start another round of printing , In this way, it becomes an endless cycle of printing .
Example 7 Design a small program to determine the current machine byte order .
#include <stdio.h>
int check_sys(int a)
{
char* p = (char*)&a;// Take variables a The address of , And cast to char* Pointer variable of type
return *p;
}
int main()
{
int a = 1;
int ret = check_sys(a);
if (ret)
printf(" The small end \n");
else
printf(" Big end \n");
return 0;
}
Thinking is judgment int Type of 4 In a space of bytes , What is the number in the lowest address . If it is 1, Explain that the storage method is 01 00 00 00 Small end storage is adopted , If it is 0, Explain that the storage method is 00 00 00 01 The big end storage mode is adopted .
Storage of floating point data
Let's start with a question :
int main()
{
int n = 9;
float* pFloat = (float*)&n;
printf("n The value of is :%d\n", n);
printf("*pFloat The value of is :%f\n", *pFloat);
*pFloat = 9.0;
printf("num The value of is :%d\n", n);
printf("*pFloat The value of is :%f\n", *pFloat);
return 0;
}
What is the result of this code ? Try to guess first .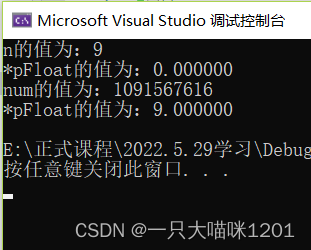
It turns out to be this , Unexpected, right ? Next, Ben meow will talk about its position and what will lead to such a result .
According to international standards IEEE( Institute of electrical and Electronic Engineering ) 754, Any binary floating point number V It can be expressed in the following form :
(-1)^S * M * 2^E
(-1)^S The sign bit , When S=0,V Is a positive number ; When S=1,V It's a negative number .
M Represents a significant number , Greater than or equal to 1, Less than 2.
2^E Indicates the index bit .E It means that the decimal point has moved a few digits , Moving left is a positive number , Moving back is a negative number .
Next, take an example to illustrate how to find S,E,M.
Decimal number :101.5
After converting to binary :1100101.1
Expressed as scientific counting :1.1001011
according to IEEE754 After the standard expression :(-1)0 * 1.1001011 * 26
Contrast the formula ,S=0,M=1.1001011,E=6.
Found S,E,M What's the use ?
Very useful , Because floating point numbers are stored in memory S,E,M Three values .
float Storage of type data
float Floating point numbers of type are single precision floating point numbers , Its size is 4 Bytes , That is to say 32 Binary bits . The following figure shows its storage model .
We put floating point numbers on it 101.5 Of S,E,M After finding it, put it in memory .
- Store S: The highest bit is the symbol bit , That is, deposit S Value . Such as 101.5 in , Stored at the top S yes 0.
- Store M:M The value of is stored in low 23 In a , Because the numerical part of any decimal can be expressed as 1.xxxxxx.
So when storing, only store M The decimal part of , That is to remove 1, Store only binary values after the decimal point .
Store from left to right ,23 Bits without values in bits are used 0 To add , It is equivalent to adding 0, It does not affect the size of the decimal value .
Such as 101.5 Store in low 23 The value in the bit is 10010110000000000000000
- Store E:E The storage of is more complex ,float Type of data is assigned to E Only 8 position , If it's all positive numbers , Its value range is 0 To 255, But we know that ,E There are negative numbers .
for example :float Data of type 0.5.
After bit binary conversion :0.1
Expressed as scientific counting :1.0
according to IEEE754 After the standard expression :(-1)0 * 1.0 *2-1
Contrast the formula :S=0,E=-1,M=1.0
There are already sign bits here ( The highest S), So use 8 Deposit E Of 8 The highest bit in the bit represents a negative number, which is obviously not very reasonable .
therefore , Found a middle number 127.
In storage E When , take E The value plus 127 Then store it S hinder 8 In a .
Such as 101.5 The most E yes 6, Add 127 The result is 133, So what is stored in these eight bits is 133 In binary form .
So after the highest position 8 In the bit is 10000101.
therefore 101.5 The image in memory is the image in the following figure 
Turn it into 16 The form of base 
Because this cat uses VS2019 The compiler uses small endian byte order storage , So the appearance in memory should be 
Let's debug , See if it's like this 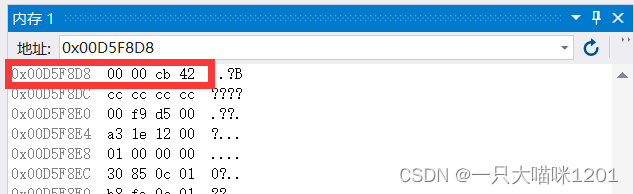
You can see , It's true .
double Storage of type data
double Floating point numbers of type are double precision floating point numbers , Its size is 8 Bytes , That is to say 64 Binary bits . The following figure shows its storage model .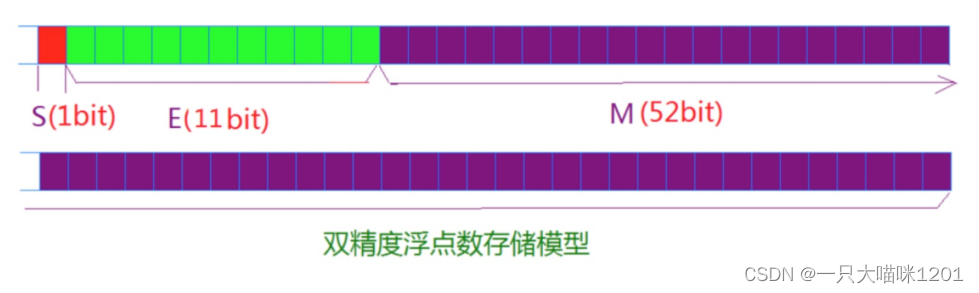
Again , We will 101.5 Set to double Floating point number of type , Is also used IEEE754 The standard will be calculated above S,E,M Put it in memory .
- Store S: And float Same type ,S There is the highest position , It's a sign bit . Such as 101.5, The highest S yes 0.
- Store M: And float Same type , Remove the integer part , Store only the decimal part , however double Type provides low 52 To store M Decimal part of , Useless bits are also used 0 Add . Such as 101.5 Store in low 52 The value in the bit is 10010110000000000000000000000000000000000000000000000000.
- Store E: And float Same type , You also need to add an intermediate value , however double The intermediate value of type is 1023, And after the highest position 11 Bits are used to store the added value . Such as 101.5 Medium E be equal to 6+1023=1029, So the one behind the highest position 11 Bits store 1029, After converting to binary, it is 10000000101.
therefore 101.5 The image in memory is the image in the following figure 
Turn it into 16 The form of base

because VS2019 The small end byte order storage method used , So its appearance in memory should be 
Let's debug , See if it's like this 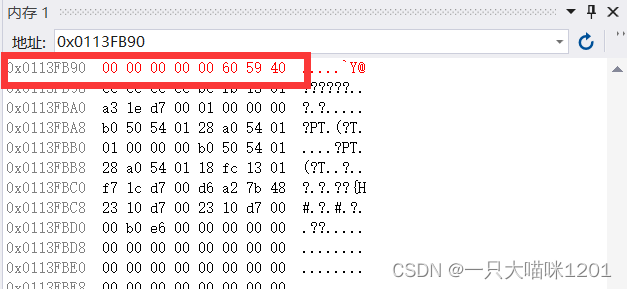
You can see , As we analyzed .
Fetch of floating point data
After we create a floating-point data , It will be stored in the memory according to the rules mentioned above . Now that you have saved it , It is used sometimes , When used, binary numbers representing floating-point numbers in memory will be retrieved , Revert to a floating point number . The rules taken out are not just the reverse of the rules put out , There are three situations when taking it out .
E Not all for 0 perhaps 1
recall ,E It represents the number of decimal places shifted left or right plus an intermediate station 127 perhaps 1023. In this case , The rule of taking out is the opposite of the rule of putting in .
- S It's a sign bit , There is the highest position , Normal removal .
- Then from the next 8 Bits or 11 Subtract the added... From the value taken from the bit 127 perhaps 1023, The result is E Value .
- Will be low 23 Bits or 52 Take out the value in bit , As a decimal part , Integer part compiler auto complement 1, The result is 1.xxxxxx
Finally take out the appearance
(-1)S * 1.xxxxxx * 2E
E All for 0
It's been worked out E Add the middle value of a positive number to form 0, Explain the original E It's a negative number , And this negative number is very small , in other words , When it was written in scientific counting mode ,E Moved right 127 Bits or 1023 position .
So it seems , Originally, this number is a very small number .
1.xxxx * 2-127 perhaps 1.xxxx * 2-1023.x Not all 0
It can be seen that , This is very small , Close to infinitesimal .
So when the compiler fetches such a number , The rule to follow is to take out a very small number .
- First S It still represents the sign bit , Normal removal .
- Take the next 8 Bits or 11 In the middle E when , The result is 1 subtract 127 perhaps 1 subtract 1023.
- Take the next 23 Bits or 52 In the middle M when , Take it out directly , And treat the extracted content as a decimal part , The compiler automatically adds a positive part 0.
Take it out
(-1)S * 0.xxxxxx * 2( A small negative number )
In this way , A very small floating-point number is taken out of memory .
E All for 1
E If it's all 1, That is to say, in memory E yes 255 Or is it 2047, So the original E Is to subtract from this value 127 perhaps 1023, The result is also a large number , That is to say, when this floating-point number is written as a scientific counting method , The decimal point moved to the left 128 Bits or 1024 position .
Then the original value of this number is very large .
1.xxxx * 2128 perhaps 1.xxxx * 21024.x Not all 0
It can be seen that , This number is very large , Close to infinity .
At this time , If the significant number M All for 0, Express ± infinity ( It depends on the sign bit s).
therefore , When the compiler takes out such a number, the rule is to take out a very large number .
These are the rules for floating-point numbers to be fetched from memory .
An example ( Skipping )
At this point, let's review the example thrown earlier
int main()
{
int n = 9;
float* pFloat = (float*)&n;
printf("n The value of is :%d\n", n);
printf("*pFloat The value of is :%f\n", *pFloat);
*pFloat = 9.0;
printf("num The value of is :%d\n", n);
printf("*pFloat The value of is :%f\n", *pFloat);
return 0;
}
Let's analyze it according to the above knowledge about the storage and retrieval of floating-point numbers .
First, I created a int Variable of type n=9, its
Original code :00000000000000000000000000001001
Inverse code :00000000000000000000000000001001
Complement code :00000000000000000000000000001001
Then take n The address of , Suppose its address is 0x00ff1240.
This address was originally a int Type of , Now force it into float Type of , Put it in the pointer variable pFloat in , So is the size 4 Bytes .
Print the first statement
printf("n The value of is :%d\n", n);What's printed is int class , Printed objects n It's also int type , So the direct result is 9.
The second print statement
printf("*pFloat The value of is :%f\n", *pFloat);Printed is a float type , Print object is pointer variable pFloat Point to the value in the address .
The value in this address is n Complement 00000000000000000000000000001001.
Because this value is needed , So you need to take it out , Because at this time standing pFloat The value in the memory space is a float Value , So take it out according to the rules of floating-point numbers .
And found that it stores E Of 8 All bits are 0, Follow the extraction rules mentioned above , The number taken out is
0.00000000000000000001001 * 2-127.
Because the default printed results are kept after the decimal point 6 position , So the result is 0.000000
And then the sentence
*pFloat = 9.0;According to the storage rules of floating point numbers 9.0 On the int Type variable n In the open space .
Floating point numbers 9.0
Written in binary 1001.0
Written as scientific counting 1.0010
S=0,E=3,M=1.0010
So the value stored in this variable space is
01000001000100000000000000000000.
The third print statement
printf("num The value of is :%d\n", n);The number to print is one int Number of types , The print object is a variable n The value in , At this point, the compiler thinks n The value in is int Type of
Complement code :01000001000100000000000000000000
Inverse code :01000001000100000000000000000000
Original code :01000001000100000000000000000000
The result of converting to decimal is 1,091,567,616.
The last print statement
printf("*pFloat The value of is :%f\n", *pFloat);The number printed is one float Data of type , The printing object is pFloat The value in the address pointed to by the pointer variable , That is to say int Type variable n The value in .
At this time, the compiler thinks that what is put in this memory space is a float Variable of type , So follow float The retrieval rules of type variables are used to retrieve this number , And print it out .
This memory space happens to be a floating-point number put in according to the floating-point number storage rules , So the printed result is the floating-point number itself .
Because floating point numbers print after the decimal point by default 6 position , So the result is 9.000000
Let's take a look at the results of the operation 
The result is consistent with our analysis above .
thus , Do you understand how floating point numbers are stored and retrieved in memory ?
summary
Integer data and floating-point data have their own storage rules in memory , Different types of data open up different sizes of space . What type of , The compiler thinks that what type is put in the corresponding space , And the size is also determined . When using variables, you should accurately use variable types , In order to avoid BUG.
If this article helps you , Please support benmew with one button three times .
边栏推荐
- 年薪50w阿裏P8親自下場,教你如何從測試進階
- Output a spiral matrix C language
- GoLand set goproxy
- Full link voltage test of the e-commerce campaign Guide
- Simulation volume leetcode [general] 1609 Parity tree
- NVIC中断优先级管理
- RuntimeError: Calculated padded input size per channel: (1 x 1). Kernel size: (5 x 5). Kernel size c
- With an annual salary of 50W, Alibaba P8 will come out in person to teach you how to advance from testing
- 数据在内存中的存储
- selenium自动化集成,八年测试经验软测工程师,一篇文章带你学懂
猜你喜欢
Greenplum 6.x monitoring software setup
UnityShader入门精要个人总结--基础篇(一)
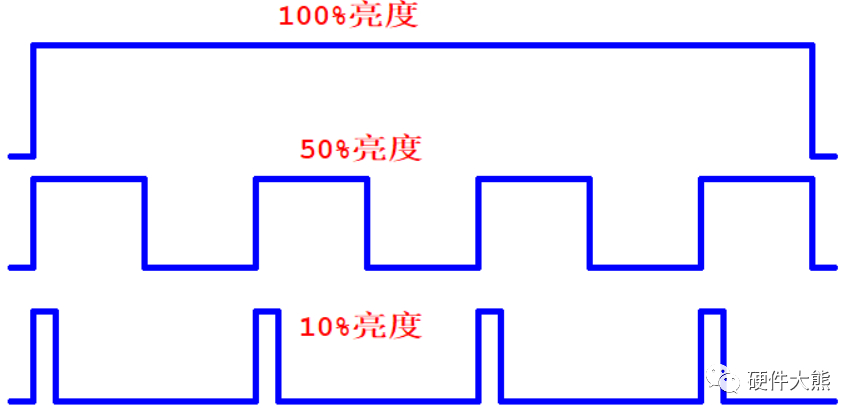
Led analog and digital dimming
![[istio introduction, architecture, components]](/img/2b/f84e5cdac6ed9b429e053ffc8dbeb0.png)
[istio introduction, architecture, components]

Expérience de port série - simple réception et réception de données
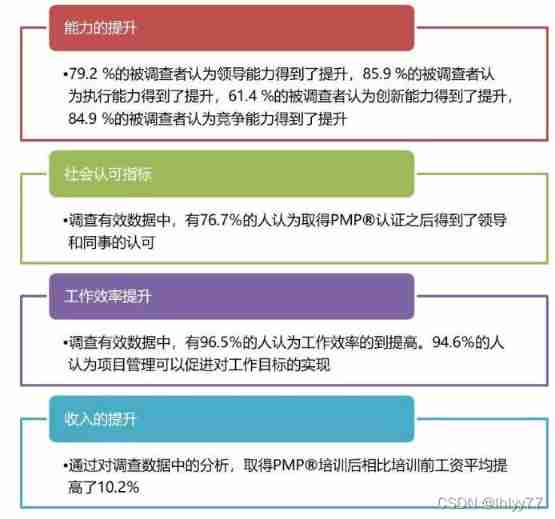
PMP Exam details after the release of the new exam outline
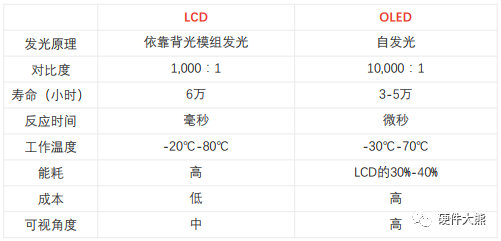
面板显示技术:LCD与OLED
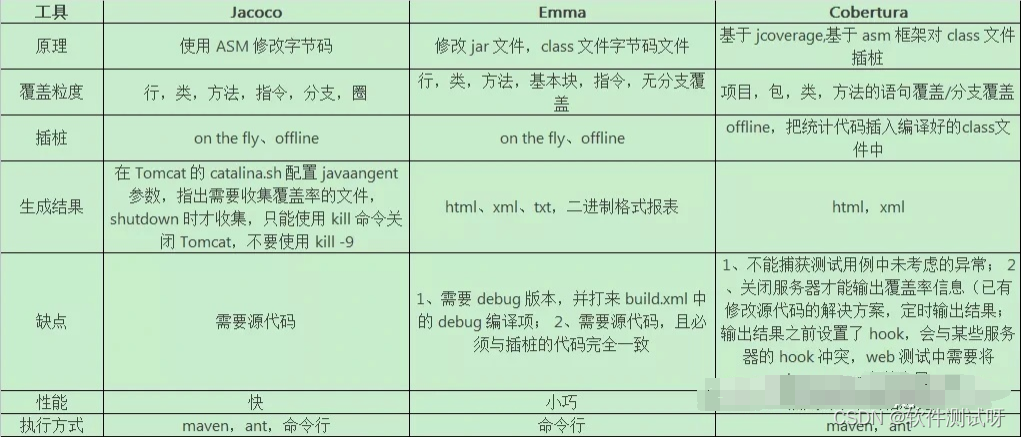
阿里p8推荐,测试覆盖率工具—Jacoco,实用性极佳
Output a spiral matrix C language
2022-06-30 unity core 8 - model import
随机推荐
What is the use of PMP certificate?
Explain Huawei's application market in detail, and gradually reduce 32-bit package applications and strategies in 2022
PPT模板、素材下载网站(纯干货,建议收藏)
PMP examination experience sharing
寄存器地址名映射
GoLand set goproxy
2022-07-06 Unity核心9——3D动画
OpenGL 3D graphics rendering
Troublesome problem of image resizing when using typora to edit markdown to upload CSDN
阿里p8手把手教你,自动化测试应该如何实现多线程?赶紧码住
Interpretation of MySQL optimization principle
面试题:高速PCB一般布局、布线原则
C language for calculating the product of two matrices
OpenGL三维图形绘制
Greenplum 6.x common statements
Alibaba P8 teaches you how to realize multithreading in automated testing? Hurry up and stop
PMP Exam Preparation experience, seek common ground while reserving differences, and successfully pass the exam
H3C vxlan configuration
Platformization, a fulcrum of strong chain complementing chain
PMP certificate preparation experience sharing