Optimal Transport系列1

鉴于Optimal Transport在Machine Learning领域的广泛使用,笔者想认真学习一下Optimal Transport,网上资料很多，但是由于笔者愚钝，找了很久才找到浅显易懂的资料。本博客旨在用最浅显的方式来描述清楚Optimal transport，由于数学能力有限，如果有讲错的地方希望各位看官能及时指正。

Prior Knowledge

L1 Distance: $d_{L_1}({\rho }_1,{\rho }_2)={\int }_{-\infty }^{+\infty }|{\rho }_1(x)-{\rho }_2(x)|dx$
KL divergence:$d_{KL}({\rho }_1||{\rho }_2)={\int }_{-\infty }^{+\infty }{\rho }_1(x)log\frac{{\rho }_1(x)}{{\rho }_2(x)}dx$
如果要衡量上图(源自参考文献1)中${\rho }_1$到${\rho }_2$的距离和${\rho }_1$到${\rho }_3$的距离，可以发现使用L1 Distance和KL divergence都失效，其算出来的都是一样的。

注意：对了L1 Distance来说，距离相同很好理解，因为其计算的就是两个分布的面积。而对于KL divergence来说，首先需要注意他不是一个距离测度，Because it is not symmetric: the KL from ${\rho }_1(x)$ to ${\rho }_2(x)$ is generally not the same as the KL from ${\rho }_1(x)$ to ${\rho }_2(x)$. Furthermore, it need not satisfy triangular inequality. 我们将Kullback-Leibler Divergence变化一下形式可得$$d_{KL}({\rho }_1||{\rho }_2)={\int }_{-\infty }^{+\infty }{\rho }_1(x)log({\rho }_1(x))-{\rho }_1(x)log({\rho }_2(x))dx$$然后把${\rho }_1(x)log({\rho }_1(x))$和${\rho }_1(x)log({\rho }_2(x))$看成两个新的分布，那么同样转化成了面积关系，由于前一项是一样的，所以主要要看后一项的差异。为了更好的理解，笔者用python写了个简单的demo：注意，这里笔者发现了一个大问题！！！

import math
import numpy as np
import matplotlib.pyplot as plt


def guassian(u, sig):
    # 均值μ, 标准差δ
    x = np.linspace(-30, 30, 1000000)   # 定义域
    y = np.exp(-(x - u) ** 2 / (2 * sig ** 2)) / (math.sqrt(2*math.pi)*sig) # 定义曲线函数
    return x, y

x1, y1 = guassian(u=0, sig=math.sqrt(1))
x2, y2 = guassian(u=1, sig=math.sqrt(1))
x3, y3 = guassian(u=2, sig=math.sqrt(1))
plt.plot(x1,y1)
plt.plot(x2,y2)
plt.plot(x3,y3)

z1 = y1 * np.log2(y1) - y1 * np.log2(y2)
z2 = y1 * np.log2(y1) - y1 * np.log2(y3)
# plt.plot(x1, z1)
# plt.plot(x1, z2)
print(np.sum(z1))
print(np.sum(z2))

通过实验发现，实验结果和预期完全不一样，我使用KL divergence计算${\rho }_1$到${\rho }_2$的距离和${\rho }_1$到${\rho }_3$的距离并不是一样的，差异很大！！！

我可视化了后一项的分布曲线，发现完全不一样，且积分后的值也完全不同。（这里我考虑到了连续变成了离散的影响，所以调过x坐标范围和画的点数，没啥区别）后来研究一下发现，文章中给的曲线貌似不是高斯分布的曲线，感觉有点被误导，所以我换了一个例子来算，虽然是离散的分布，但是还是能比较直观的反映问题的（PS,这里其实很好奇为啥用高斯分布会不行，有大佬知道原因吗）：

可以发现对于上述的分布，L1 Distance和KL divergence都失效了。

Optimal Transport

上一节讲了L1 Distance和KL divergence存在的问题，本节将详细描述Optimal Transport，首先定义问题。Optimal Transport的核心在于如何找到一个最优转化将一个分布转化为另一个分布，且要使得转化损失最小。（注意：这里的分布可以是连续或者离散的）这里用上图中的${\rho }_1$和${\rho }_2$举例：
为了方便理解，我们可以将${\rho }_1$和${\rho }_2$想象成一堆沙子，那么Optimal Transport问题就变成了如何把${\rho }_1$形状的沙子堆成${\rho }_2$的样子，且做功要最小。$\pi (x,y)$代表从x位置搬多少质量的沙子到y位置，那么显然${\rho }_1(x)$表示x位置总共有多少质量的沙子（大白话就是x位置曲线的高度）。所以问题就可以用下式来表示：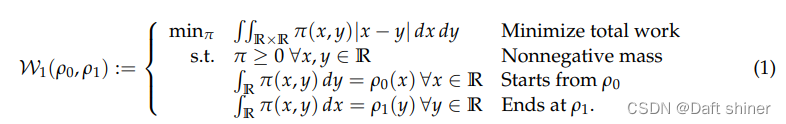

其中目标函数为搬运做功最小，因为搬运沙子的质量要大于等于0，所以约束的第一条也好理解，至于第二和第三条，是满足它初始和最终的分布。This amount of work is known as the 1-Wasserstein distance in optimal transport。接下来把他泛化到p-Wasserstein distance:

同样比较好理解，只是运输的距离发生了改变。问题定义完了以后，那么如何才能求得这个$\pi (x,y)$呢？

Discrete Problems in One Dimension

对于一维问题有以上两种情况：D2D，D2C。对于D2D的数据，我们首先松弛原有的分布函数$\rho (x)$到${\mu }_0,{\mu }_1\in Prob(\mathbb{R})$，Define the Dirac $\delta$-measure centered at $x\in \mathbb{R}$ via (:=在数学中表示为定义为)
$${\delta }_x(S):=\{\begin{array}{ll}1,& ifx\in S\\ 0,& Otherwise.\end{array}$$此时${\mu }_0,{\mu }_1$分别为：

其中${\sum }_i{a}_{0i}={\sum }_i{a}_{1i}=1$,$a_{0i},a_{1i}\ge 0$。个人认为这里的$S$是$[x_{01},x_{02},\cdots ,x_{0k_0}]$的子集。这时问题的计算为：

同样和上面的解释方法一样，$T_{ij}$表示从$x_{0i}$运输到$x_{1j}$的质量。$|x_{0i}-x_{1j}{|}^p$是从$x_{0i}$运输到$x_{1j}$的距离。$T_{ij}$运输质量要大于等于0，$x_{0i}$和$x_{1j}$处的质量要满足守恒条件。要求$T_{ij}$，这是一个有限元的线性规划，可以使用许多经典算法求解，例如 simplex or interior point methods。而对于D2C的情况，每个离散的${\mu }_0$都映射到一段连续的区间${\mu }_1$,如下图所示：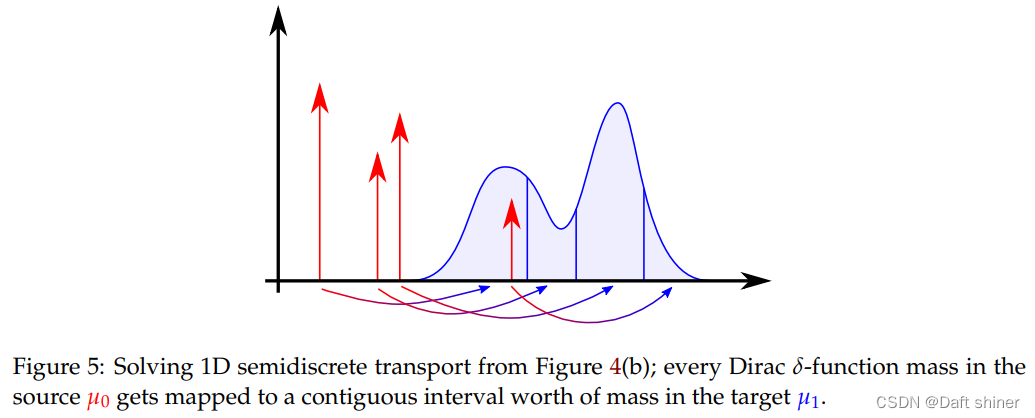

Conclusion

本节主要讲了Optimal Transport的两种形式（D2C,D2D),下一节将介绍其更加general的形式。

References

[1] Optimal Transport on Discrete Domains
[2] Kullback-Leibler Divergence
[3] Optimal Transport and Wasserstein Distance